Difference between revisions of "Trigonometric identities"
Mysmartmouth (talk | contribs) |
(basic/reciprocal) |
||
| Line 1: | Line 1: | ||
| − | Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them: | + | '''Trigonometric identities''' are used to manipulate trig equations in certain ways. Here is a list of them: |
| + | == Basic Definitions == | ||
| + | The six basic trigonometric functions can be defined using a right triangle: | ||
| − | == Reciprocal | + | <center>[[Image:righttriangle.png]]</center> |
| + | |||
| + | The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses <math>\csc</math>). They are defined as follows: | ||
| + | |||
| + | {| style="width:75%; height:200px; margin: 1em auto 1em auto" border="0" | ||
| + | |- | ||
| + | | <math>\sin A = \frac ac</math> || <math>\csc A = \frac ca</math> | ||
| + | |- | ||
| + | | <math> \cos A = \frac bc</math> || <math>\sec A = \frac cb</math> | ||
| + | |- | ||
| + | | <math> \tan A = \frac ab</math> || <math> \cot A = \frac ba</math> | ||
| + | |} | ||
| + | |||
| + | == Reciprocal Relations == | ||
| + | From the last section, it is easy to see that the following hold: | ||
| + | |||
| + | {| style="width:75%; margin: 1em auto 1em auto" | ||
| + | |- | ||
| + | | <math> \sin A = \frac 1{\csc A}</math> || <math> \cos A = \frac 1{\sec A}</math> || <math> \tan A = \frac 1{\cot A}</math> | ||
| + | |} | ||
== Pythagorean Identities == | == Pythagorean Identities == | ||
| Line 22: | Line 43: | ||
*<math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}</math> | *<math>|1-e^{i\theta}|=2\sin\frac{\theta}{2}</math> | ||
| − | |||
| − | |||
==See also== | ==See also== | ||
Revision as of 07:34, 24 June 2006
Trigonometric identities are used to manipulate trig equations in certain ways. Here is a list of them:
Contents
Basic Definitions
The six basic trigonometric functions can be defined using a right triangle:
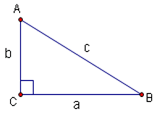
The six trig functions are sine, cosine, tangent, cosecant, secant, and cotangent. They are abbreviated by using the first three letters of their name (except for cosecant which uses ![]() ). They are defined as follows:
). They are defined as follows:
Reciprocal Relations
From the last section, it is easy to see that the following hold:
Pythagorean Identities
Angle Addition Identities
Even-Odd Identities
Prosthaphaersis Indentities
(Otherwise known as sum-to-product identities)
Other Identities
See also
This article is a stub. Help us out by expanding it.









