Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus
GET READY FOR THE AMC 12 WITH AoPS
Learn with outstanding instructors and top-scoring students from around the world in our AMC 12 Problem Series online course.
CHECK SCHEDULE

Difference between revisions of "2003 AMC 12A Problems"

(→‎Problem 13)
m (→‎Problem 13)
Line 95: Line 95:
  
 
== Problem 13 ==
 
== Problem 13 ==
−
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with all faces missing?  
+
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?  
  
 
[[Image:2003amc10a10.gif]]
 
[[Image:2003amc10a10.gif]]

Revision as of 15:36, 31 December 2011

Problem 1

What is the difference between the sum of the first $2003$ even counting numbers and the sum of the first $2003$ odd counting numbers?

$\mathrm{(A) \ } 0\qquad \mathrm{(B) \ } 1\qquad \mathrm{(C) \ } 2\qquad \mathrm{(D) \ } 2003\qquad \mathrm{(E) \ } 4006$

Solution

Problem 2

Members of the Rockham Soccer League buy socks and T-shirts. Socks cost $4 per pair and each T-shirt costs $5 more than a pair of socks. Each member needs one pair of socks and a shirt for home games and another pair of socks and a shirt for away games. If the total cost is $2366, how many members are in the League?

$\mathrm{(A) \ } 77\qquad \mathrm{(B) \ } 91\qquad \mathrm{(C) \ } 143\qquad \mathrm{(D) \ } 182\qquad \mathrm{(E) \ } 286$

Solution

Problem 3

A solid box is $15$ cm by $10$ cm by $8$ cm. A new solid is formed by removing a cube $3$ cm on a side from each corner of this box. What percent of the original volume is removed?

$\mathrm{(A) \ } 4.5\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 18\qquad \mathrm{(E) \ } 24$

Solution

Problem 4

It takes Mary $30$ minutes to walk uphill $1$ km from her home to school, but it takes her only $10$ minutes to walk from school to her home along the same route. What is her average speed, in km/hr, for the round trip?

$\mathrm{(A) \ } 3\qquad \mathrm{(B) \ } 3.125\qquad \mathrm{(C) \ } 3.5\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 4.5$

Solution

Problem 5

The sum of the two 5-digit numbers $AMC10$ and $AMC12$ is $123422$. What is $A+M+C$?

$\mathrm{(A) \ } 10\qquad \mathrm{(B) \ } 11\qquad \mathrm{(C) \ } 12\qquad \mathrm{(D) \ } 13\qquad \mathrm{(E) \ } 14$

Solution

Problem 6

Define $x \heartsuit y$ to be $|x-y|$ for all real numbers $x$ and $y$. Which of the following statements is not true?

$\mathrm{(A) \ } x \heartsuit y = y \heartsuit x$ for all $x$ and $y$

$\mathrm{(B) \ } 2(x \heartsuit y) = (2x) \heartsuit (2y)$ for all $x$ and $y$

$\mathrm{(C) \ } x \heartsuit 0 = x$ for all $x$

$\mathrm{(D) \ } x \heartsuit x = 0$ for all $x$

$\mathrm{(E) \ } x \heartsuit y > 0$ if $x \neq y$

Solution

Problem 7

How many non-congruent triangles with perimeter $7$ have integer side lengths?

$\mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 3\qquad \mathrm{(D) \ } 4\qquad \mathrm{(E) \ } 5$

Solution

Problem 8

What is the probability that a randomly drawn positive factor of $60$ is less than $7$?

$\mathrm{(A) \ } \frac{1}{10}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{1}{4}\qquad \mathrm{(D) \ } \frac{1}{3}\qquad \mathrm{(E) \ } \frac{1}{2}$

Solution

Problem 9

A set $S$ of points in the $xy$-plane is symmetric about the orgin, both coordinate axes, and the line $y=x$. If $(2,3)$ is in $S$, what is the smallest number of points in $S$?

$\mathrm{(A) \ } 1\qquad \mathrm{(B) \ } 2\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 8\qquad \mathrm{(E) \ } 16$

Solution

Problem 10

Al, Bert, and Carl are the winners of a school drawing for a pile of Halloween candy, which they are to divide in a ratio of $3:2:1$, respectively. Due to some confusion they come at different times to claim their prizes, and each assumes he is the first to arrive. If each takes what he believes to be the correct share of candy, what fraction of the candy goes unclaimed?

$\mathrm{(A) \ } \frac{1}{18}\qquad \mathrm{(B) \ } \frac{1}{6}\qquad \mathrm{(C) \ } \frac{2}{9}\qquad \mathrm{(D) \ } \frac{5}{18}\qquad \mathrm{(E) \ } \frac{5}{12}$

Solution

Problem 11

A square and an equilateral triangle have the same perimeter. Let $A$ be the area of the circle circumscribed about the square and $B$ the area of the circle circumscribed around the triangle. Find $A/B$.

$\mathrm{(A) \ } \frac{9}{16}\qquad \mathrm{(B) \ } \frac{3}{4}\qquad \mathrm{(C) \ } \frac{27}{32}\qquad \mathrm{(D) \ } \frac{3\sqrt{6}}{8}\qquad \mathrm{(E) \ } 1$

Solution

Problem 12

Sally has five red cards numbered $1$ through $5$ and four blue cards numbered $3$ through $6$. She stacks the cards so that the colors alternate and so that the number on each red card divides evenly into the number on each neighboring blue card. What is the sum of the numbers on the middle three cards?

$\mathrm{(A) \ } 8\qquad \mathrm{(B) \ } 9\qquad \mathrm{(C) \ } 10\qquad \mathrm{(D) \ } 11\qquad \mathrm{(E) \ } 12$

Solution

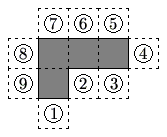
Problem 13

The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?

2003amc10a10.gif

$\mathrm{(A) \ } 2\qquad \mathrm{(B) \ } 3\qquad \mathrm{(C) \ } 4\qquad \mathrm{(D) \ } 5\qquad \mathrm{(E) \ } 6$

Solution

Problem 14

Points $K, L, M,$ and $N$ lie in the plane of the square $ABCD$ such that $AKB$, $BLC$, $CMD$, and $DNA$ are equilateral triangles. If $ABCD$ has an area of 16, find the area of $KLMN$.

[asy] unitsize(2cm); defaultpen(fontsize(8)+linewidth(0.8)); pair A=(-0.5,0.5), B=(0.5,0.5), C=(0.5,-0.5), D=(-0.5,-0.5); pair K=(0,1.366), L=(1.366,0), M=(0,-1.366), N=(-1.366,0); draw(A--N--K--A--B--K--L--B--C--L--M--C--D--M--N--D--A); label("$A$",A,SE); label("$B$",B,SW); label("$C$",C,NW); label("$D$",D,NE); label("$K$",K,NNW); label("$L$",L,E); label("$M$",M,S); label("$N$",N,W); [/asy]

$\textrm{(A)}\ 32\qquad\textrm{(B)}\ 16+16\sqrt{3}\qquad\textrm{(C)}\ 48\qquad\textrm{(D)}\ 32+16\sqrt{3}\qquad\textrm{(E)}\ 64$

Solution

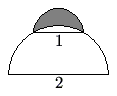
Problem 15

A semicircle of diameter $1$ sits at the top of a semicircle of diameter $2$, as shown. The shaded area inside the smaller semicircle and outside the larger semicircle is called a lune. Determine the area of this lune.

2003amc10a19.gif

$\mathrm{(A) \ } \frac{1}{6}\pi-\frac{\sqrt{3}}{4}\qquad \mathrm{(B) \ } \frac{\sqrt{3}}{4}-\frac{1}{12}\pi\qquad \mathrm{(C) \ } \frac{\sqrt{3}}{4}-\frac{1}{24}\pi\qquad \mathrm{(D) \ } \frac{\sqrt{3}}{4}+\frac{1}{24}\pi\qquad \mathrm{(E) \ } \frac{\sqrt{3}}{4}+\frac{1}{12}\pi$

Solution

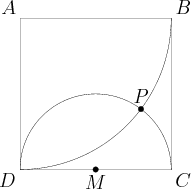
Problem 16

A point P is chosen at random in the interior of equilateral triangle $ABC$. What is the probability that $\triangle ABP$ has a greater area than each of $\triangle ACP$ and $\triangle BCP$?

$\textbf{(A)}\ \frac{1}{6}\qquad\textbf{(B)}\ \frac{1}{4}\qquad\textbf{(C)}\ \frac{1}{3}\qquad\textbf{(D)}\ \frac{1}{2}\qquad\textbf{(E)}\ \frac{2}{3}$

Solution

Problem 17

Square $ABCD$ has sides of length $4$, and $M$ is the midpoint of $\overline{CD}$. A circle with radius $2$ and center $M$ intersects a circle with radius $4$ and center $A$ at points $P$ and $D$. What is the distance from $P$ to $\overline{AD}$?

5d50417537c6cddfb70810403c62787b889cdcb1.png

$\textbf{(A)}\ 3 \qquad \textbf{(B)}\ \frac {16}{5} \qquad \textbf{(C)}\ \frac {13}{4} \qquad \textbf{(D)}\ 2\sqrt {3} \qquad \textbf{(E)}\ \frac {7}{2}$

Solution

Problem 18

Let $n$ be a $5$-digit number, and let $q$ and $r$ be the quotient and the remainder, respectively, when $n$ is divided by $100$. For how many values of $n$ is $q+r$ divisible by $11$?

$\mathrm{(A) \ } 8180\qquad \mathrm{(B) \ } 8181\qquad \mathrm{(C) \ } 8182\qquad \mathrm{(D) \ } 9000\qquad \mathrm{(E) \ } 9090$

Solution

Problem 19

A parabola with equation $y=ax^2+bx+c$ is reflected about the $x$-axis. The parabola and its reflection are translated horizontally five units in opposite directions to become the graphs of $y=f(x)$ and $y=g(x)$, respectively. Which of the following describes the graph of $y=(f+g)x$?

$\textbf{(A)}\ \text{a parabola tangent to the }x\text{-axis}$ $\textbf{(B)}\ \text{a parabola not tangent to the }x\text{-axis}\qquad\textbf{(C)}\ \text{a horizontal line}$ $\textbf{(D)}\ \text{a non-horizontal line}\qquad\textbf{(E)}\ \text{the graph of a cubic function}$

Solution

Problem 20

How many $15$-letter arrangements of $5$ A's, $5$ B's, and $5$ C's have no A's in the first $5$ letters, no B's in the next $5$ letters, and no C's in the last $5$ letters?

$\textrm{(A)}\ \sum_{k=0}^{5}\binom{5}{k}^{3}\qquad\textrm{(B)}\ 3^{5}\cdot 2^{5}\qquad\textrm{(C)}\ 2^{15}\qquad\textrm{(D)}\ \frac{15!}{(5!)^{3}}\qquad\textrm{(E)}\ 3^{15}$

Solution

Problem 21

The graph of the polynomial

$P(x) = x^5 + ax^4 + bx^3 + cx^2 + dx + e$

has five distinct $x$-intercepts, one of which is at $(0,0)$. Which of the following coefficients cannot be zero?

$\textbf{(A)}\ a \qquad \textbf{(B)}\ b \qquad \textbf{(C)}\ c \qquad \textbf{(D)}\ d \qquad \textbf{(E)}\ e$

Solution

Problem 22

Objects $A$ and $B$ move simultaneously in the coordinate plane via a sequence of steps, each of length one. Object $A$ starts at $(0,0)$ and each of its steps is either right or up, both equally likely. Object $B$ starts at $(5,7)$ and each of its steps is either to the left or down, both equally likely. Which of the following is closest to the probability that the objects meet?

$\mathrm{(A)} \ 0.10 \qquad \mathrm{(B)} \ 0.15 \qquad \mathrm{(C)} \ 0.20 \qquad \mathrm{(D)} \ 0.25 \qquad \mathrm{(E)} \ 0.30 \qquad$


Solution

Problem 23

How many perfect squares are divisors of the product $1! \cdot 2! \cdot 3! \cdot \hdots \cdot 9!$?

$\textbf{(A)}\ 504\qquad\textbf{(B)}\ 672\qquad\textbf{(C)}\ 864\qquad\textbf{(D)}\ 936\qquad\textbf{(E)}\ 1008$

Solution

Problem 24

If $a\geq b > 1,$ what is the largest possible value of $\log_{a}(a/b) + \log_{b}(b/a)?$

$\mathrm{(A)}\ -2 \qquad \mathrm{(B)}\ 0 \qquad \mathrm{(C)}\ 2 \qquad \mathrm{(D)}\ 3 \qquad \mathrm{(E)}\ 4$

Solution

Problem 25

Let $f(x)= \sqrt{ax^2+bx}$. For how many real values of $a$ is there at least one positive value of $b$ for which the domain of $f$ and the range $f$ are the same set?

$\mathrm{(A) \ 0 } \qquad \mathrm{(B) \ 1 } \qquad \mathrm{(C) \ 2 } \qquad \mathrm{(D) \ 3 } \qquad \mathrm{(E) \ \mathrm{infinitely \ many} }$

Solution

See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2003_AMC_12A_Problems&oldid=44049"