Difference between revisions of "1971 Canadian MO Problems"
Airplanes1 (talk | contribs) (→Problem 6) |
Airplanes1 (talk | contribs) (→Problem 5) |
||
| Line 29: | Line 29: | ||
== Problem 5 == | == Problem 5 == | ||
| − | + | Let <math>p(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x+a_0</math>, where the coefficients <math> a_i</math> are integers. If <math>p(0)</math> and <math>p(1)</math> are both odd, show that <math>p(x)</math> has no integral roots. | |
Revision as of 21:49, 13 December 2011
This is an empty template page which needs to be filled. You can help us out by finding the needed content and editing it in. Thanks.
Contents
Problem 1
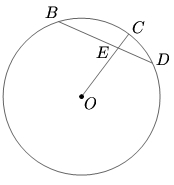
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Problem 2
Let ![]() and
and ![]() be positive real numbers such that
be positive real numbers such that ![]() . Show that
. Show that ![]() .
.
Problem 3
![]() is a quadrilateral with
is a quadrilateral with ![]() . If
. If ![]() is greater than
is greater than ![]() , prove that
, prove that ![]() .
.
Problem 4
Determine all real numbers ![]() such that the two polynomials
such that the two polynomials ![]() and
and ![]() have at least one root in common.
have at least one root in common.
Problem 5
Let ![]() , where the coefficients
, where the coefficients ![]() are integers. If
are integers. If ![]() and
and ![]() are both odd, show that
are both odd, show that ![]() has no integral roots.
has no integral roots.
Problem 6
Show that, for all integers ![]() ,
, ![]() is not a multiple of 121.
Solution
is not a multiple of 121.
Solution