Difference between revisions of "1971 Canadian MO Problems"
Airplanes1 (talk | contribs) |
Airplanes1 (talk | contribs) (→Problem 6) |
||
| Line 36: | Line 36: | ||
== Problem 6 == | == Problem 6 == | ||
| + | Show that, for all integers <math>n</math>, <math>n^2+2n+12</math> is not a multiple of 121. | ||
| + | [[1971 Canadian MO Problems/Problem 6 | Solution]] | ||
| − | |||
== Problem 7 == | == Problem 7 == | ||
Revision as of 21:47, 13 December 2011
This is an empty template page which needs to be filled. You can help us out by finding the needed content and editing it in. Thanks.
Contents
Problem 1
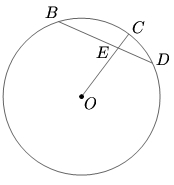
![]() is a chord of a circle such that
is a chord of a circle such that ![]() and
and ![]() Let
Let ![]() be the center of the circle. Join
be the center of the circle. Join ![]() and extend
and extend ![]() to cut the circle at
to cut the circle at ![]() Given
Given ![]() find the radius of the circle
find the radius of the circle
Problem 2
Let ![]() and
and ![]() be positive real numbers such that
be positive real numbers such that ![]() . Show that
. Show that ![]() .
.
Problem 3
![]() is a quadrilateral with
is a quadrilateral with ![]() . If
. If ![]() is greater than
is greater than ![]() , prove that
, prove that ![]() .
.
Problem 4
Determine all real numbers ![]() such that the two polynomials
such that the two polynomials ![]() and
and ![]() have at least one root in common.
have at least one root in common.
Problem 5
Problem 6
Show that, for all integers ![]() ,
, ![]() is not a multiple of 121.
Solution
is not a multiple of 121.
Solution