Difference between revisions of "Stewart's Theorem"
m (Reverted edits by Solafidefarms (Solafidefarms); changed back to last version by Agolsme) |
|||
| Line 1: | Line 1: | ||
== Statement == | == Statement == | ||
| − | ' | + | <center>[[Image:Stewart's_theorem.png]]</center> |
| − | If a [[cevian]] of length | + | |
| − | + | If a [[cevian]] of length d is drawn and divides side a into segments m and n, then | |
| + | |||
| + | <center><math> cnc + bmb = man + dad.</math></center> | ||
| + | |||
== Proof == | == Proof == | ||
| − | For this proof we will use the law of cosines and the identity <math>\cos{\theta} = -\cos{180 - \theta}</math>. | + | For this proof we will use the law of cosines and the identity <math>\cos{\theta} = -\cos{(180 - \theta)}</math>. |
| − | Label the triangle <math>ABC</math> with a cevian extending from <math>A</math> onto <math>BC</math>, label that point <math>D</math>. Let CA = n Let DB = m. Let AD = | + | Label the triangle <math>ABC</math> with a cevian extending from <math>A</math> onto <math>BC</math>, label that point <math>D</math>. Let CA = n Let DB = m. Let AD = d. We can write two equations: |
| − | *<math> n^{2} + | + | *<math> n^{2} + d^{2} - nd\cos{\angle CDA} = b^{2} </math> |
| − | *<math> m^{2} + | + | *<math> m^{2} + d^{2} + md\cos{\angle CDA} = c^{2} </math> |
When we write everything in terms of cos(CDA) we have: | When we write everything in terms of cos(CDA) we have: | ||
| − | *<math> \frac{n^2 + | + | *<math> \frac{n^2 + d^2 - b^2}{nd} = \cos{\angle CDA}</math> |
| − | *<math> \frac{c^2 - m^2 - | + | *<math> \frac{c^2 - m^2 -d^2}{md} = \cos{\angle CDA}</math> |
| − | |||
| − | |||
| − | |||
| − | |||
| − | = | + | Now we set the two equal and arrive at Stewart's theorem: <math> c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n </math> |
| − | |||
== See also == | == See also == | ||
* [[Menelaus' Theorem]] | * [[Menelaus' Theorem]] | ||
* [[Ceva's Theorem]] | * [[Ceva's Theorem]] | ||
| + | * [[Geometry]] | ||
| + | * [[Angle Bisector Theorem]] | ||
Revision as of 20:35, 23 June 2006
Statement
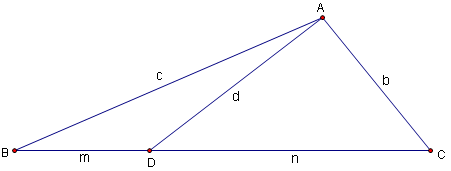
If a cevian of length d is drawn and divides side a into segments m and n, then
Proof
For this proof we will use the law of cosines and the identity ![]() .
.
Label the triangle ![]() with a cevian extending from
with a cevian extending from ![]() onto
onto ![]() , label that point
, label that point ![]() . Let CA = n Let DB = m. Let AD = d. We can write two equations:
. Let CA = n Let DB = m. Let AD = d. We can write two equations:
When we write everything in terms of cos(CDA) we have:
Now we set the two equal and arrive at Stewart's theorem: ![]()









