Difference between revisions of "2010 AMC 10B Problems/Problem 20"
AceOfClubs (talk | contribs) m (→Solution) |
m (see also box) |
||
| Line 28: | Line 28: | ||
The letter answer is '''D''' | The letter answer is '''D''' | ||
| + | |||
| + | ==See Also== | ||
| + | {{AMC10 box|year=2010|ab=B|num-b=19|num-a=21}} | ||
Revision as of 21:52, 25 November 2011
Problem
Two circles lie outside regular hexagon 
. The first is tangent to $\overbar{AB}$ (Error compiling LaTeX. Unknown error_msg), and the second is tangent to $\overbar{DE}$ (Error compiling LaTeX. Unknown error_msg). Both are tangent to lines 
and 
. What is the ratio of the area of the second circle to that of the first circle?
Solution
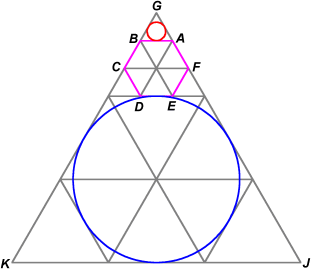
A good diagram here is very helpful.
The first circle is in red, the second in blue.
With this diagram, we can see that the first circle is inscribed in equilateral triangle 
while the second circle is inscribed in 
.
From this, it's evident that the ratio of the red area to the blue area is equal to the ratio of the areas of triangles to
Since the ratio of areas is equal to the square of the ratio of lengths, we know our final answer is 
From the diagram, we can see that this is 
The letter answer is D
See Also
| 2010 AMC 10B (Problems • Answer Key • Resources) | ||
| Preceded by Problem 19 |
Followed by Problem 21 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
