Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2002 AMC 12B Problems/Problem 20"
Line 1: Line 1:
 +
{{duplicate|[[2002 AMC 12B Problems|2002 AMC 12B #20]] and [[2002 AMC 10B Problems|2002 AMC 10B #22]]}}
 
== Problem ==
 
== Problem ==
 
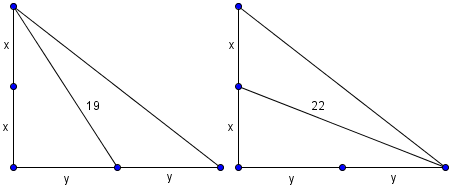
Let <math>\triangle XOY</math> be a [[right triangle|right-angled triangle]] with <math>m\angle XOY = 90^{\circ}</math>. Let <math>M</math> and <math>N</math> be the [[midpoint]]s of legs <math>OX</math> and <math>OY</math>, respectively. Given that <math>XN = 19</math> and <math>YM = 22</math>, find <math>XY</math>.
 
Let <math>\triangle XOY</math> be a [[right triangle|right-angled triangle]] with <math>m\angle XOY = 90^{\circ}</math>. Let <math>M</math> and <math>N</math> be the [[midpoint]]s of legs <math>OX</math> and <math>OY</math>, respectively. Given that <math>XN = 19</math> and <math>YM = 22</math>, find <math>XY</math>.
Line 20: Line 21:
 
By the Pythagorean Theorem again, we have  
 
By the Pythagorean Theorem again, we have  
  
−
<cmath>(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = 26 \Rightarrow \mathrm{(B)}</cmath>
+
<cmath>(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = \boxed{\mathrm{(B)}\ 26}</cmath>
  
 
== See also ==
 
== See also ==
 +
{{AMC10 box|year=2002|ab=B|num-b=21|num-a=23}}
 
{{AMC12 box|year=2002|ab=B|num-b=19|num-a=21}}
 
{{AMC12 box|year=2002|ab=B|num-b=19|num-a=21}}
 +
 +
[[Category:Introductory Geometry Problems]]

Revision as of 15:28, 29 July 2011

The following problem is from both the 2002 AMC 12B #20 and 2002 AMC 10B #22, so both problems redirect to this page.

Problem

Let $\triangle XOY$ be a right-angled triangle with $m\angle XOY = 90^{\circ}$. Let $M$ and $N$ be the midpoints of legs $OX$ and $OY$, respectively. Given that $XN = 19$ and $YM = 22$, find $XY$.

$\mathrm{(A)}\ 24 \qquad\mathrm{(B)}\ 26 \qquad\mathrm{(C)}\ 28 \qquad\mathrm{(D)}\ 30 \qquad\mathrm{(E)}\ 32$

Solution

2002 12B AMC-20.png

Let $OM = x$, $ON = y$. By the Pythagorean Theorem on $\triangle XON, MOY$ respectively, \begin{align*} (2x)^2 + y^2 &= 19^2\\ x^2 + (2y)^2 &= 22^2\end{align*}

Summing these gives $5x^2 + 5y^2 = 845 \Longrightarrow x^2 + y^2 = 169$.

By the Pythagorean Theorem again, we have

\[(2x)^2 + (2y)^2 = XY^2 \Longrightarrow XY = \sqrt{4(x^2 + y^2)} = \boxed{\mathrm{(B)}\ 26}\]

See also

2002 AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2002 AMC 12B (Problems • Answer Key • Resources)
Preceded by
Problem 19 		Followed by
Problem 21
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2002_AMC_12B_Problems/Problem_20&oldid=40906"