Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1995 AIME Problems/Problem 9"

(→‎Solution)
(tex fixes)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
Triangle <math>\displaystyle ABC</math> is isosceles, with <math>\displaystyle AB=AC</math> and altitude <math>\displaystyle AM=11.</math>  Suppose that there is a point <math>\displaystyle D</math> on <math>\displaystyle \overline{AM}</math> with <math>\displaystyle AD=10</math> and <math>\displaystyle \angle BDC=3\angle BAC.</math>  Then the perimeter of <math>\displaystyle \triangle ABC</math> may be written in the form <math>\displaystyle a+\sqrt{b},</math> where <math>\displaystyle a</math> and <math>\displaystyle b</math> are integers.  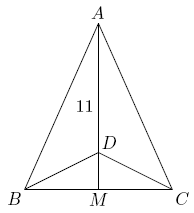Find <math>\displaystyle a+b.</math>
+
Triangle <math>ABC</math> is [[isosceles triangle|isosceles]], with <math>AB=AC</math> and [[altitude]] <math>AM=11.</math>  Suppose that there is a point <math>D</math> on <math>\overline{AM}</math> with <math>AD=10</math> and <math>\angle BDC=3\angle BAC.</math>  Then the perimeter of <math>\triangle ABC</math> may be written in the form <math>a+\sqrt{b},</math> where <math>a</math> and <math>b</math> are integers.  Find <math>a+b.</math>
  
−
[[Image:AIME_1995_Problem_9.png]]
+
[[Image:AIME_1995_Problem_9.png|center]]
  
 
== Solution ==
 
== Solution ==
 +
Let <math>x=\angle CAM</math>, so <math>3x=\angle CDM</math>. Then, <math>\frac{\tan 3x}{\tan x}=\frac{CM/1}{CM/11}=11</math>. Expanding <math>\tan 3x</math> using the angle sum identity gives <cmath>\tan 3x=\tan(2x+x)=\frac{3\tan x-\tan^3x}{1-3\tan^2x}.</cmath> Thus, <math>\frac{3-\tan^2x}{1-3\tan^2x}=11</math>. Solving, we get <math>\tan x= \frac 12</math>. Hence, <math>CM=\frac{11}2</math> and <math>AC= \frac{11\sqrt{5}}2</math> by the [[Pythagorean Theorem]]. The total perimeter is <math>2(AC + CM) = \sqrt{605}+11</math>. The answer is thus <math>a+b=\boxed{616}</math>.
  
−
Let <math>\angle CAM=x</math>, <math>\angle CDM=3x</math>. Then, <math>(tan 3x)/(tan x)=(CM/1)/(CM/11)=11</math>. Expanding tan 3x using the angle sum formula gives <math>tan 3x=(3tan x-tan^3x)/(1-3tan^2x)</math>. Thus, <math>(3-tan^2x)/(1-3tan^2x)=11</math>. Solving, we get <math>tan x=1/2</math>. Hence, <math>CM=11/2</math> and AC=<math>11\sqrt{5}/2</math> by Pythag. The total perimeter is double the sum of these, which is <math>\sqrt{605}+11</math>. The answer is then <math>616</math>.
+
== See also ==
 +
{{AIME box|year=1995|num-b=8|num-a=10}}
  
−
== See also ==
+
[[Category:Intermediate Geometry Problems]]
−
* [[1995_AIME_Problems/Problem_8|Previous Problem]]
+
[[Category:Intermediate Trigonometry Problems]]
−
* [[1995_AIME_Problems/Problem_10|Next Problem]]
 
−
* [[1995 AIME Problems]]
 

Revision as of 11:42, 18 June 2008

Problem

Triangle $ABC$ is isosceles, with $AB=AC$ and altitude $AM=11.$ Suppose that there is a point $D$ on $\overline{AM}$ with $AD=10$ and $\angle BDC=3\angle BAC.$ Then the perimeter of $\triangle ABC$ may be written in the form $a+\sqrt{b},$ where $a$ and $b$ are integers. Find $a+b.$

AIME 1995 Problem 9.png

Solution

Let $x=\angle CAM$, so $3x=\angle CDM$. Then, $\frac{\tan 3x}{\tan x}=\frac{CM/1}{CM/11}=11$. Expanding $\tan 3x$ using the angle sum identity gives \[\tan 3x=\tan(2x+x)=\frac{3\tan x-\tan^3x}{1-3\tan^2x}.\] Thus, $\frac{3-\tan^2x}{1-3\tan^2x}=11$. Solving, we get $\tan x= \frac 12$. Hence, $CM=\frac{11}2$ and $AC= \frac{11\sqrt{5}}2$ by the Pythagorean Theorem. The total perimeter is $2(AC + CM) = \sqrt{605}+11$. The answer is thus $a+b=\boxed{616}$.

See also

1995 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 8 		Followed by
Problem 10
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1995_AIME_Problems/Problem_9&oldid=26667"