Difference between revisions of "2003 AMC 10A Problems/Problem 10"
(→Solution) |
(→Solution) |
||
| Line 21: | Line 21: | ||
Thus the answer is <math>6 \Rightarrow E</math>. | Thus the answer is <math>6 \Rightarrow E</math>. | ||
| − | Another way to think of it is that a cube missing one | + | Another way to think of it is that a cube missing one face has <math>5</math> of it's <math>6</math> faces. Since the shape has <math>4</math> faces already, we need another face. The only way to add anopther face is if the added square does not overlap any of the others. <math>1</math>,<math>2</math>, and <math>3</math> overlap, while <math>4 \Rightarrow</math> 9 do not. The answer is <math>6 \Rightarrow E</math> |
== See Also == | == See Also == | ||
Revision as of 18:01, 3 June 2008
Problem
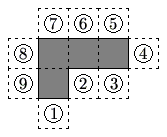
The polygon enclosed by the solid lines in the figure consists of 4 congruent squares joined edge-to-edge. One more congruent square is attached to an edge at one of the nine positions indicated. How many of the nine resulting polygons can be folded to form a cube with one face missing?
![]()
Solution
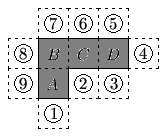
Let the squares be labeled ![]() ,
, ![]() ,
, ![]() , and
, and ![]() .
.
When the polygon is folded, the "right" edge of square ![]() becomes adjacent to the "bottom edge" of square
becomes adjacent to the "bottom edge" of square ![]() , and the "bottom" edge of square
, and the "bottom" edge of square ![]() becomes adjacent to the "bottom" edge of square
becomes adjacent to the "bottom" edge of square ![]() .
.
So, any "new" square that is attached to those edges will prevent the polygon from becoming a cube with one face missing.
Therefore, squares ![]() ,
, ![]() , and
, and ![]() will prevent the polygon from becoming a cube with one face missing.
will prevent the polygon from becoming a cube with one face missing.
Squares ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() will allow the polygon to become a cube with one face missing when folded.
will allow the polygon to become a cube with one face missing when folded.
Thus the answer is ![]() .
.
Another way to think of it is that a cube missing one face has ![]() of it's
of it's ![]() faces. Since the shape has
faces. Since the shape has ![]() faces already, we need another face. The only way to add anopther face is if the added square does not overlap any of the others.
faces already, we need another face. The only way to add anopther face is if the added square does not overlap any of the others. ![]() ,
,![]() , and
, and ![]() overlap, while
overlap, while ![]() 9 do not. The answer is
9 do not. The answer is ![]()
See Also
| 2003 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||