Difference between revisions of "2003 AMC 12A Problems/Problem 17"
(→Problem) |
(→Solution) |
||
| Line 46: | Line 46: | ||
Solving each factor for 0 yields <math>x = 0 , \frac{16}{5}</math>. The first value of <math>0</math> is obviously referring to the point where the circles intersect at the origin, <math>D</math>, so the second value must be referring to the x value of the coordinate of <math>P</math>. Since <math>\overline{AD}</math> is the y-axis, the distance to it from <math>P</math> is the same as the x-value of the coordinate of <math>P</math>, so the distance from <math>P</math> to <math>\overline{AD}</math> is <math>\frac{16}{5} \Rightarrow B</math> | Solving each factor for 0 yields <math>x = 0 , \frac{16}{5}</math>. The first value of <math>0</math> is obviously referring to the point where the circles intersect at the origin, <math>D</math>, so the second value must be referring to the x value of the coordinate of <math>P</math>. Since <math>\overline{AD}</math> is the y-axis, the distance to it from <math>P</math> is the same as the x-value of the coordinate of <math>P</math>, so the distance from <math>P</math> to <math>\overline{AD}</math> is <math>\frac{16}{5} \Rightarrow B</math> | ||
| + | |||
| + | == See Also == | ||
| + | *[[2003 AMC 12A Problems]] | ||
| + | *[[2003 AMC 12A/Problem 16|Previous Problem]] | ||
| + | *[[2003 AMC 12A/Problem 18|Next Problem]] | ||
Revision as of 19:54, 31 May 2008
Problem
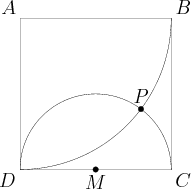
Square ![]() has sides of length
has sides of length ![]() , and
, and ![]() is the midpoint of
is the midpoint of ![]() . A circle with radius
. A circle with radius ![]() and center
and center ![]() intersects a circle with raidus
intersects a circle with raidus ![]() and center
and center ![]() at points
at points ![]() and
and ![]() . What is the distance from
. What is the distance from ![]() to
to ![]() ?
?
![]()
Solution
Let ![]() be the origin.
be the origin. ![]() is the point
is the point ![]() and
and ![]() is the point
is the point ![]() . We are given the radius of the quarter circle and semicircle as
. We are given the radius of the quarter circle and semicircle as ![]() and
and ![]() , respectively, so their equations, respectively, are:
, respectively, so their equations, respectively, are:
![]()
![]()
Algebraically manipulating the second equation gives:
![]()
![]()
![]()
![]()
Substituting this back into the first equation:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Solving each factor for 0 yields ![]() . The first value of
. The first value of ![]() is obviously referring to the point where the circles intersect at the origin,
is obviously referring to the point where the circles intersect at the origin, ![]() , so the second value must be referring to the x value of the coordinate of
, so the second value must be referring to the x value of the coordinate of ![]() . Since
. Since ![]() is the y-axis, the distance to it from
is the y-axis, the distance to it from ![]() is the same as the x-value of the coordinate of
is the same as the x-value of the coordinate of ![]() , so the distance from
, so the distance from ![]() to
to ![]() is
is ![]()