Difference between revisions of "Squeeze Theorem"
m (Squeeze Play Theorem moved to Squeeze Theorem over redirect) |
m |
||
| Line 1: | Line 1: | ||
{{WotWAnnounce|week=May 4-11}} | {{WotWAnnounce|week=May 4-11}} | ||
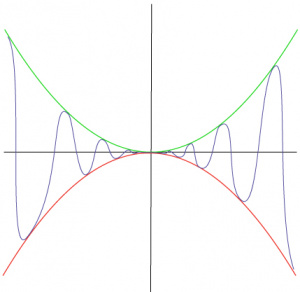
| − | The '''Squeeze | + | The '''Squeeze Theorem''' (also called the '''Sandwich Theorem''' or the '''Squeeze Play Theorem''') is a relatively simple [[theorem]] that deals with [[calculus]], specifically [[limit]]s. |
[[Image:Squeeze theorem example.jpg|thumb|Squeeze Theorem]] | [[Image:Squeeze theorem example.jpg|thumb|Squeeze Theorem]] | ||
Revision as of 19:07, 4 May 2008
| This is an AoPSWiki Word of the Week for May 4-11 |
The Squeeze Theorem (also called the Sandwich Theorem or the Squeeze Play Theorem) is a relatively simple theorem that deals with calculus, specifically limits.
Theorem
Suppose ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() . If
. If ![]() and
and ![]() approach some common limit L as
approach some common limit L as ![]() approaches
approaches ![]() , then
, then ![]() .
.
Proof
If ![]() is between
is between ![]() and
and ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() , then either
, then either ![]() or
or ![]() for all
for all ![]() in the neighborhood of
in the neighborhood of ![]() . Since the second case is basically the first case, we just need to prove the first case.
. Since the second case is basically the first case, we just need to prove the first case.
If ![]() increases to
increases to ![]() , then
, then ![]() goes to either
goes to either ![]() or
or ![]() , where
, where ![]() . If
. If ![]() decreases to
decreases to ![]() , then
, then ![]() goes to either
goes to either ![]() or
or ![]() , where
, where ![]() . Since
. Since ![]() can't go to
can't go to ![]() or
or ![]() , then
, then ![]() must go to
must go to ![]() . Therefore,
. Therefore, ![]() .
.