Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 12B Problems/Problem 12"

(Created blank page)
 
(Made page)
Line 1: Line 1:
 +
==Problem==
 +
Let <math>z</math> be a complex number with real part greater than <math>1</math> and <math>|z|=2</math>. In the complex plane, the four points <math>0</math>, <math>z</math>, <math>z^2</math>, and <math>z^3</math> are the vertices of a quadrilateral with area <math>15</math>. What is the imaginary part of <math>z</math>?
  
 +
==Diagram==
 +
 +
[[File:2024_12B_Q12.png|400px]]
 +
 +
==Solution 1 (similar triangles)==
 +
 +
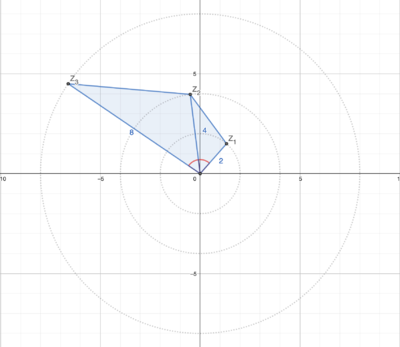
By making a rough estimate of where <math>z</math>, <math>z^2</math>, and <math>z^3</math> are on the complex plane, we can draw a pretty accurate diagram (like above.)
 +
 +
Here, points <math>Z_1</math>, <math>Z_2</math>, and <math>Z_3</math> lie at the coordinates of <math>z</math>, <math>z^2</math>, and <math>z^3</math> respectively, and <math>O</math> is the origin.
 +
 +
We're given <math>|z|=2</math>, so <math>|z^2|=|z|^2=4</math> and <math>|z^3|=|z|^3 = 8</math>. This gives us <math>OZ_1=2</math>, <math>OZ_2=4</math>, and <math>OZ_3=8</math>.
 +
 +
Additionally, we know that <math>\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}</math> (since every power of <math>z</math> rotates around the origin by the same angle.) We set these angles equal to <math>\theta</math>.
 +
 +
This gives us enough info to say that <math>\triangle{OZ_1Z_2}\sim\triangle{OZ_2Z_3}</math> by SAS (since <math>\frac{OZ_2}{OZ_1}=\frac{OZ_3}{OZ_2}=2</math>.)
 +
 +
It follows that <math>[OZ_1Z_2Z_3]=[OZ_1Z_2]+[OZ_2Z_3]=[OZ_1Z_2]+2^2[OZ_1Z_2]=5[OZ_1Z_2]</math> as the ratio of side lengths of the two triangles is 2 to 1.
 +
 +
This means <math>5[OZ_1Z_2]=15</math> or <math>[OZ_1Z_2]=3</math> as we were given <math>[OZ_1Z_2Z_3]=15</math>.
 +
 +
Using <math>A=\frac{a*b*sinC}{2}</math>, we get that <math>[OZ_1Z_2]=\frac{2*4*sin(\theta)}{2}=4sin(\theta)</math>, so <math>4sin(\theta)=3</math>, giving <math>sin(\theta)=\frac{3}{4}</math>.
 +
 +
Thus, <math>Im(z)=|z|sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(B) }\frac{3}{2}}</math>.
 +
 +
~nm1728

Revision as of 01:37, 14 November 2024

Problem

Let $z$ be a complex number with real part greater than $1$ and $|z|=2$. In the complex plane, the four points $0$, $z$, $z^2$, and $z^3$ are the vertices of a quadrilateral with area $15$. What is the imaginary part of $z$?

Diagram

2024 12B Q12.png

Solution 1 (similar triangles)

By making a rough estimate of where $z$, $z^2$, and $z^3$ are on the complex plane, we can draw a pretty accurate diagram (like above.)

Here, points $Z_1$, $Z_2$, and $Z_3$ lie at the coordinates of $z$, $z^2$, and $z^3$ respectively, and $O$ is the origin.

We're given $|z|=2$, so $|z^2|=|z|^2=4$ and $|z^3|=|z|^3 = 8$. This gives us $OZ_1=2$, $OZ_2=4$, and $OZ_3=8$.

Additionally, we know that $\angle{Z_1OZ_2}\cong\angle{Z_2OZ_3}$ (since every power of $z$ rotates around the origin by the same angle.) We set these angles equal to $\theta$.

This gives us enough info to say that $\triangle{OZ_1Z_2}\sim\triangle{OZ_2Z_3}$ by SAS (since $\frac{OZ_2}{OZ_1}=\frac{OZ_3}{OZ_2}=2$.)

It follows that $[OZ_1Z_2Z_3]=[OZ_1Z_2]+[OZ_2Z_3]=[OZ_1Z_2]+2^2[OZ_1Z_2]=5[OZ_1Z_2]$ as the ratio of side lengths of the two triangles is 2 to 1.

This means $5[OZ_1Z_2]=15$ or $[OZ_1Z_2]=3$ as we were given $[OZ_1Z_2Z_3]=15$.

Using $A=\frac{a*b*sinC}{2}$, we get that $[OZ_1Z_2]=\frac{2*4*sin(\theta)}{2}=4sin(\theta)$, so $4sin(\theta)=3$, giving $sin(\theta)=\frac{3}{4}$.

Thus, $Im(z)=|z|sin(\theta)=2(\frac{3}{4})=\boxed{\textbf{(B) }\frac{3}{2}}$.

~nm1728

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_12B_Problems/Problem_12&oldid=233638"