Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2024 AMC 10A Problems/Problem 25"

m
(→‎Solution)
Line 19: Line 19:
 
<math>\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196</math>
 
<math>\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196</math>
  
−
==Solution==
+
==Solution 1==
 
Call the first row <math>A</math> and the second row <math>B</math>. To cross over from <math>A</math> to <math>B</math>, we must touch two boxes during each cross, and we will cross twice. We can cross at the first column or the second column on the left side, and the eighth column or the ninth column on the right side. For each crossing case, the remaining boxes not touched (<math>6,5,5,4</math> boxes depending on the crossing points) can be touched at either the top or the bottom but not both, so there are <math>2^n</math> cases for <math>n</math> remaining boxes. Thus there are <math>2^6+2^5+2^5+2^4=144</math> cases. However, we have forgotten the case where the loop only resides in <math>A</math> or only in <math>B</math>, so the final count is <math>144+2=\boxed{\textbf{(C) }146}</math>.
 
Call the first row <math>A</math> and the second row <math>B</math>. To cross over from <math>A</math> to <math>B</math>, we must touch two boxes during each cross, and we will cross twice. We can cross at the first column or the second column on the left side, and the eighth column or the ninth column on the right side. For each crossing case, the remaining boxes not touched (<math>6,5,5,4</math> boxes depending on the crossing points) can be touched at either the top or the bottom but not both, so there are <math>2^n</math> cases for <math>n</math> remaining boxes. Thus there are <math>2^6+2^5+2^5+2^4=144</math> cases. However, we have forgotten the case where the loop only resides in <math>A</math> or only in <math>B</math>, so the final count is <math>144+2=\boxed{\textbf{(C) }146}</math>.
  
 
~eevee9406
 
~eevee9406
 +
 +
==Solution 2==
 +
(In principal, this is essentially the same method as Solution 1, but here I want to elaborate and make things clearer)
 +
 +
Observations:
 +
 +
1. You can't have a vertical line in any place other than the first and second columns and the last and second-to-last columns.
 +
2. You can you a box around the top row or along the bottom row, otherwise all the solutions have a vertical line at the first and second columns and the last and second-to-last columns.
 +
 +
Thus, Using casework, we can split this problem into 4 cases. However, we can focus on only the first one for right now.
 +
 +
For case 1, we assume that the green lines shown below are given (always have toothpicks on them)
 +
 +
[[Image:Scrasdfasd.png|600px]]
 +
 +
However, we cannot go horizontally onto the left or rightmost square with a "1" on it (Then, there will be multiple toothpicks on that square), Thus, need to place toothpicks on the red lines here:
 +
[[Image:Screenshot 2024-11-08 192200.png|600px]]
 +
 +
And the only toothpicks we can place that will connect to the red lines are to go horizontally inward:
 +
 +
[[Image:Screenshot 2024-11-08 192516.png|600px]]
 +
 +
Now, concentrate on the first row of squares. A toothpick can be placed on either the bottom or top and connected to a continuous squiggle by adding vertical toothpicks, for example,
 +
 +
[[Image:Screenshot 2024-11-08 193401.png|600px]]
 +
 +
How many squiggles are possible?
 +
 +
[[Image:Screenshot 2024-11-08 194804.png|600px]]
 +
 +
We can summarize this by giving a high squiggle position a 1 and a low position a 0, thus we have a 6-digit binary sequence. Thus, we can have <math>2^6=64</math> ways to make this squiggle.
 +
 +
Case 2: We can also, as the observations state, pull in one of the sides, thus we can have a squiggle with 5 binary digits. only utilizing the first 7 columns:
 +
 +
[[Image:Screenshot 2024-11-08 195135.png|600px]]
 +
 +
Here, we only have 5 binary digits to work with, so there are <math>2^5=32</math> ways to make this squiggle.
 +
 +
Case 3: Similarly, we can utilize the last 7 columns.
 +
 +
[[Image:Screenshot 2024-11-08 195553.png|600px]]
 +
 +
Again, we only have 5 binary digits to work with, so there are <math>2^5=32</math> ways to make this squiggle.
 +
 +
Case 4: We can use an even smaller section. Using only the middle 6 columns gives us a 4-wide squiggle:
 +
 +
[[Image:Screenshot 2024-11-08 195945.png|600px]]
 +
 +
Thus, there are <math>2^4=16</math> ways to make this squiggle.
 +
 +
Adding up all our cases: <math>64+32+32+16=144</math>
 +
 +
However, there are two more ways to draw a qualifying shape:
 +
 +
[[Image:Screenshot 2024-11-08 200416.png|600px]]
 +
 +
We can draw a rectangle like that in the first row or third row. Thus, we have a grand total of
 +
<math>144+2=\boxed{\textbf{(C) }146}</math> ways.
 +
 +
 +
A note to (potential) editors:
 +
This answer was not made to be concise or especially professional. It was made to explicitly explain this problem in a way so that it is easy to understand and follow.
 +
 +
~hermanboxcar5
  
 
==See also==
 
==See also==

Revision as of 23:08, 8 November 2024

The following problem is from both the 2024 AMC 10A #25 and 2024 AMC 12A #22, so both problems redirect to this page.

Problem

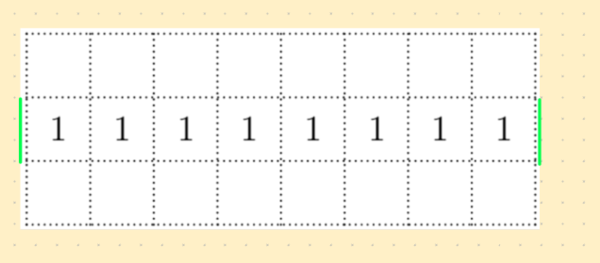
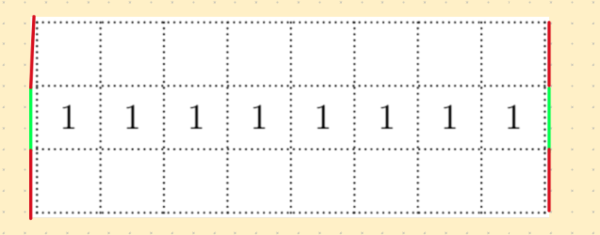
The figure below shows a dotted grid $8$ cells wide and $3$ cells tall consisting of $1''\times1''$ squares. Carl places $1$-inch toothpicks along some of the sides of the squares to create a closed loop that does not intersect itself. The numbers in the cells indicate the number of sides of that square that are to be covered by toothpicks, and any number of toothpicks are allowed if no number is written. In how many ways can Carl place the toothpicks? [asy] size(6cm); for (int i=0; i<9; ++i) { draw((i,0)--(i,3),dotted); } for (int i=0; i<4; ++i){ draw((0,i)--(8,i),dotted); } for (int i=0; i<8; ++i) { for (int j=0; j<3; ++j) { if (j==1) { label("1",(i+0.5,1.5)); }}} [/asy] $\textbf{(A) }130\qquad\textbf{(B) }144\qquad\textbf{(C) }146\qquad\textbf{(D) }162\qquad\textbf{(E) }196$

Solution 1

Call the first row $A$ and the second row $B$. To cross over from $A$ to $B$, we must touch two boxes during each cross, and we will cross twice. We can cross at the first column or the second column on the left side, and the eighth column or the ninth column on the right side. For each crossing case, the remaining boxes not touched ($6,5,5,4$ boxes depending on the crossing points) can be touched at either the top or the bottom but not both, so there are $2^n$ cases for $n$ remaining boxes. Thus there are $2^6+2^5+2^5+2^4=144$ cases. However, we have forgotten the case where the loop only resides in $A$ or only in $B$, so the final count is $144+2=\boxed{\textbf{(C) }146}$.

~eevee9406

Solution 2

(In principal, this is essentially the same method as Solution 1, but here I want to elaborate and make things clearer)

Observations:

1. You can't have a vertical line in any place other than the first and second columns and the last and second-to-last columns. 2. You can you a box around the top row or along the bottom row, otherwise all the solutions have a vertical line at the first and second columns and the last and second-to-last columns.

Thus, Using casework, we can split this problem into 4 cases. However, we can focus on only the first one for right now.

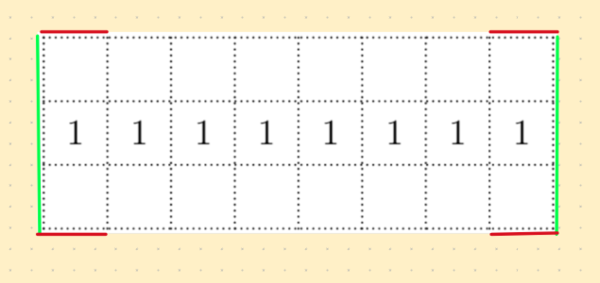
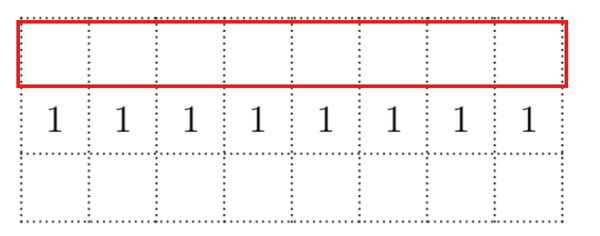
For case 1, we assume that the green lines shown below are given (always have toothpicks on them)

Scrasdfasd.png

However, we cannot go horizontally onto the left or rightmost square with a "1" on it (Then, there will be multiple toothpicks on that square), Thus, need to place toothpicks on the red lines here: Screenshot 2024-11-08 192200.png

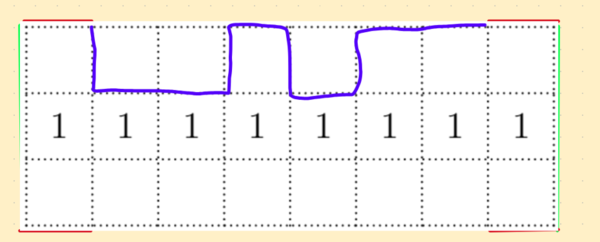
And the only toothpicks we can place that will connect to the red lines are to go horizontally inward:

Screenshot 2024-11-08 192516.png

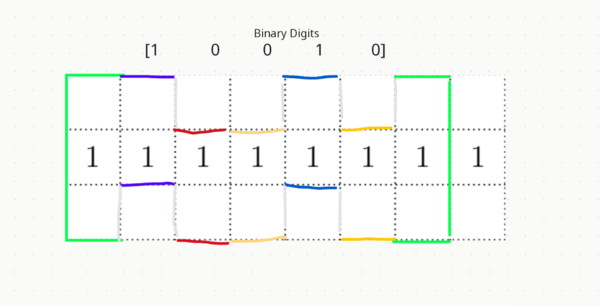
Now, concentrate on the first row of squares. A toothpick can be placed on either the bottom or top and connected to a continuous squiggle by adding vertical toothpicks, for example,

Screenshot 2024-11-08 193401.png

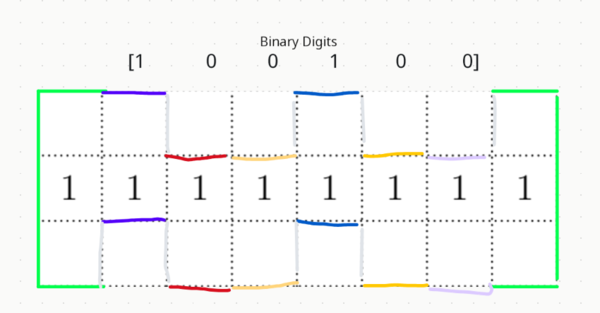
How many squiggles are possible?

Screenshot 2024-11-08 194804.png

We can summarize this by giving a high squiggle position a 1 and a low position a 0, thus we have a 6-digit binary sequence. Thus, we can have $2^6=64$ ways to make this squiggle.

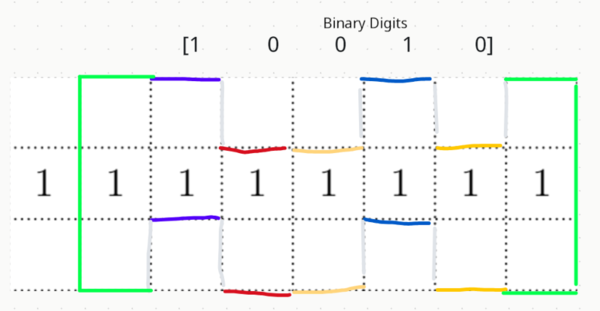
Case 2: We can also, as the observations state, pull in one of the sides, thus we can have a squiggle with 5 binary digits. only utilizing the first 7 columns:

Screenshot 2024-11-08 195135.png

Here, we only have 5 binary digits to work with, so there are $2^5=32$ ways to make this squiggle.

Case 3: Similarly, we can utilize the last 7 columns.

Screenshot 2024-11-08 195553.png

Again, we only have 5 binary digits to work with, so there are $2^5=32$ ways to make this squiggle.

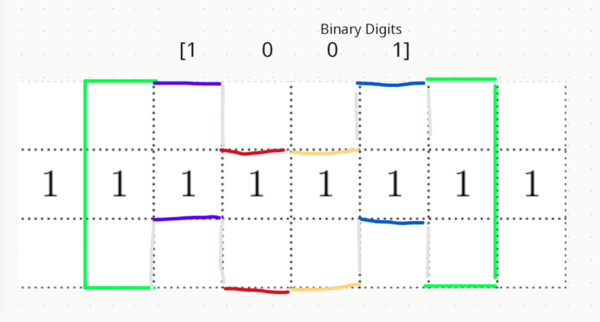
Case 4: We can use an even smaller section. Using only the middle 6 columns gives us a 4-wide squiggle:

Screenshot 2024-11-08 195945.png

Thus, there are $2^4=16$ ways to make this squiggle.

Adding up all our cases: $64+32+32+16=144$

However, there are two more ways to draw a qualifying shape:

Screenshot 2024-11-08 200416.png

We can draw a rectangle like that in the first row or third row. Thus, we have a grand total of $144+2=\boxed{\textbf{(C) }146}$ ways.


A note to (potential) editors: This answer was not made to be concise or especially professional. It was made to explicitly explain this problem in a way so that it is easy to understand and follow.

~hermanboxcar5

See also

2024 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Problem
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
2024 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2024_AMC_10A_Problems/Problem_25&oldid=232418"