Difference between revisions of "1985 AJHSME Problem 24"
(→Solution 2) |
|||
| Line 26: | Line 26: | ||
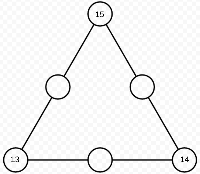
Figure 1 | Figure 1 | ||
| − | Then, we can label the left empty circle as <math>a</math> and the right empty circle as <math>a-1,</math> because 14 is one more than 13, and we need to balance it out for the sum to be the same. The bottom empty circle can be named as <math>a+1</math> because <math>13+14=15+13-1.</math> We only can use the numbers <math>10, 11,</math> and <math>12</math> now, so <math>a=11,</math> <math>a+1=12,</math> and <math>a-1=10.</math> Therefore, the largest value for <math>S</math> is <math>15+11+13=10\cdot3+(5+3+1)=\boxed{ | + | Then, we can label the left empty circle as <math>a</math> and the right empty circle as <math>a-1,</math> because 14 is one more than 13, and we need to balance it out for the sum to be the same. The bottom empty circle can be named as <math>a+1</math> because <math>13+14=15+13-1.</math> We only can use the numbers <math>10, 11,</math> and <math>12</math> now, so <math>a=11,</math> <math>a+1=12,</math> and <math>a-1=10.</math> Therefore, the largest value for <math>S</math> is <math>15+11+13=10\cdot3+(5+3+1)=\boxed{\textbf{(D)}~39}.</math> |
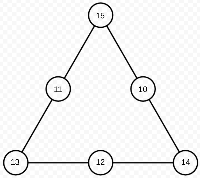
But, we have to make sure that all three sides sum to 39. The completed triangle is shown in Figure 2. | But, we have to make sure that all three sides sum to 39. The completed triangle is shown in Figure 2. | ||
| Line 32: | Line 32: | ||
[[File:24 fig2.png]] | [[File:24 fig2.png]] | ||
Figure 2 | Figure 2 | ||
| + | |||
| + | ~ Edited by [[User:Aoum|Aoum]] | ||
Latest revision as of 20:18, 23 February 2025
Problem
In a magic triangle, each of the six whole numbers 
is placed in one of the circles so that the sum, 
, of the three numbers on each side of the triangle is the same. The largest possible value for is
![[asy] draw(circle((0,0),1)); draw(dir(60)--6*dir(60)); draw(circle(7*dir(60),1)); draw(8*dir(60)--13*dir(60)); draw(circle(14*dir(60),1)); draw((1,0)--(6,0)); draw(circle((7,0),1)); draw((8,0)--(13,0)); draw(circle((14,0),1)); draw(circle((10.5,6.0621778264910705273460621952706),1)); draw((13.5,0.86602540378443864676372317075294)--(11,5.1961524227066318805823390245176)); draw((10,6.9282032302755091741097853660235)--(7.5,11.258330249197702407928401219788)); [/asy]](http://latex.artofproblemsolving.com/8/3/4/83415da2658f8c65d5efcd1a4cc144e572e5a2a0.png)
Solution 1
A numeral can appear in a maximum of 2 sides in this triangle, so we can put the largest 3 numbers, 15, 14, and 13 at the corners, as shown in Figure 1.
Figure 1
Then, we can label the left empty circle as 
and the right empty circle as 
because 14 is one more than 13, and we need to balance it out for the sum to be the same. The bottom empty circle can be named as 
because 
We only can use the numbers 
and 
now, so 
and 
Therefore, the largest value for is 
But, we have to make sure that all three sides sum to 39. The completed triangle is shown in Figure 2.
Figure 2
~ Edited by Aoum
