Difference between revisions of "2024 AIME II Problems/Problem 8"
m (→Problem) |
(→Solution 1) |
||
| Line 107: | Line 107: | ||
~Prof_Joker | ~Prof_Joker | ||
| + | ==Solution 2== | ||
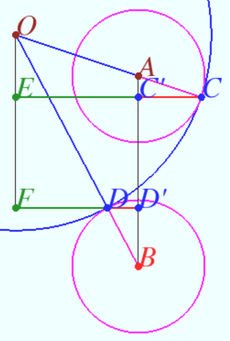
| + | [[File:2024 AIME II 8.png|230px|right]] | ||
| + | <cmath>OC = OD = 11, AC = BD = 3, EC' = FD' = 6.</cmath> | ||
| + | <cmath>\frac {CC'}{C'E} = \frac{AC}{OA} \implies CC' = \frac {3 \cdot 6}{11-3}</cmath> | ||
| + | <cmath>\frac {DD'}{DB} = \frac{FD'}{OB} \implies DD' = \frac {3 \cdot 6}{11+3}</cmath> | ||
| + | <cmath>CC' + DD' = \frac {9}{4}+\frac {9}{7} = \frac {99}{28}.</cmath> | ||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==Video Solution== | ==Video Solution== | ||
Revision as of 15:18, 23 April 2024
Problem
Torus ![]() is the surface produced by revolving a circle with radius
is the surface produced by revolving a circle with radius ![]() around an axis in the plane of the circle that is a distance
around an axis in the plane of the circle that is a distance ![]() from the center of the circle (so like a donut). Let
from the center of the circle (so like a donut). Let ![]() be a sphere with a radius
be a sphere with a radius ![]() . When
. When ![]() rests on the inside of
rests on the inside of ![]() , it is internally tangent to
, it is internally tangent to ![]() along a circle with radius
along a circle with radius ![]() , and when
, and when ![]() rests on the outside of
rests on the outside of ![]() , it is externally tangent to
, it is externally tangent to ![]() along a circle with radius
along a circle with radius ![]() . The difference
. The difference ![]() can be written as
can be written as ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
![[asy] unitsize(0.3 inch); draw(ellipse((0,0), 3, 1.75)); draw((-1.2,0.1)..(-0.8,-0.03)..(-0.4,-0.11)..(0,-0.15)..(0.4,-0.11)..(0.8,-0.03)..(1.2,0.1)); draw((-1,0.04)..(-0.5,0.12)..(0,0.16)..(0.5,0.12)..(1,0.04)); draw((0,2.4)--(0,-0.15)); draw((0,-0.15)--(0,-1.75), dashed); draw((0,-1.75)--(0,-2.25)); draw(ellipse((2,0), 1, 0.9)); draw((2.03,-0.02)--(2.9,-0.4)); [/asy]](http://latex.artofproblemsolving.com/d/4/7/d47e4fdb4c54afd9a0eabe569e4cabb139ec600a.png)
Solution 1
First, let's consider a section ![]() of the solids, along the axis.
By some 3D-Geomerty thinking, we can simply know that the axis crosses the sphere center. So, that is saying, the
of the solids, along the axis.
By some 3D-Geomerty thinking, we can simply know that the axis crosses the sphere center. So, that is saying, the ![]() we took crosses one of the equator of the sphere.
we took crosses one of the equator of the sphere.
Here I drew two graphs, the first one is the case when ![]() is internally tangent to
is internally tangent to ![]() ,
,
![[asy] unitsize(0.35cm); pair O = (0, 0); real r1 = 11; real r2 = 3; draw(circle(O, r1)); pair A = O + (0, -r1); pair B = O + (0, r1); draw(A--B); pair C = O + (0, -1.25*r1); pair D = O + (0, 1.25*r1); draw(C--D, dashed); dot(O); pair E = (2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)); pair F = (0, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)); pair G = (-r2 * O + r1 * E) / (r1 - r2); pair H = (-r2 * O + r1 * F) / (r1 - r2); draw(circle(E, r2)); draw(circle((-2 * r2, -sqrt((r1 - r2) * (r1 - r2) - 4 * r2 * r2)), r2)); draw(O--G, dashed); draw(F--E, dashed); draw(G--H, dashed); label("$O$", O, SW); label("$A$", A, SW); label("$B$", B, NW); label("$C$", C, NW); label("$D$", D, SW); label("$E_i$", E, NE); label("$F_i$", F, W); label("$G_i$", G, SE); label("$H_i$", H, W); label("$r_i$", 0.5 * H + 0.5 * G, NE); label("$3$", 0.5 * E + 0.5 * G, NE); label("$11$", 0.5 * O + 0.5 * G, NE); [/asy]](http://latex.artofproblemsolving.com/d/5/d/d5d1bcb73ba68266bd9d518d4246fe3974b37fef.png)
and the second one is when ![]() is externally tangent to
is externally tangent to ![]() .
.
![[asy] unitsize(0.35cm); pair O = (0, 0); real r1 = 11; real r2 = 3; draw(circle(O, r1)); pair A = O + (0, -r1); pair B = O + (0, r1); draw(A--B); pair C = O + (0, -1.25*(r1 + r2)); pair D = O + (0, 1.25*r1); draw(C--D, dashed); dot(O); pair E = (2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)); pair F = (0, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)); pair G = (r2 * O + r1 * E) / (r1 + r2); pair H = (r2 * O + r1 * F) / (r1 + r2); draw(circle(E, r2)); draw(circle((-2 * r2, -sqrt((r1 + r2) * (r1 + r2) - 4 * r2 * r2)), r2)); draw(O--E, dashed); draw(F--E, dashed); draw(G--H, dashed); label("$O$", O, SW); label("$A$", A, SW); label("$B$", B, NW); label("$C$", C, NW); label("$D$", D, SW); label("$E_o$", E, NE); label("$F_o$", F, SW); label("$G_o$", G, S); label("$H_o$", H, W); label("$r_o$", 0.5 * H + 0.5 * G, NE); label("$3$", 0.5 * E + 0.5 * G, NE); label("$11$", 0.5 * O + 0.5 * G, NE); [/asy]](http://latex.artofproblemsolving.com/2/f/b/2fb5d4d1ae5297959727a179a10ed94e72e66dc5.png)
For both graphs, point ![]() is the center of sphere
is the center of sphere ![]() , and points
, and points ![]() and
and ![]() are the intersections of the sphere and the axis. Point
are the intersections of the sphere and the axis. Point ![]() (ignoring the subscripts) is one of the circle centers of the intersection of torus
(ignoring the subscripts) is one of the circle centers of the intersection of torus ![]() with section
with section ![]() . Point
. Point ![]() (again, ignoring the subscripts) is one of the tangents between the torus
(again, ignoring the subscripts) is one of the tangents between the torus ![]() and sphere
and sphere ![]() on section
on section ![]() .
. ![]() ,
, ![]() .
.
And then, we can start our calculation.
In both cases, we know ![]() .
.
Hence, in the case of internal tangent, ![]() .
.
In the case of external tangent, ![]() .
.
Thereby, ![]() . And there goes the answer,
. And there goes the answer, ![]()
~Prof_Joker
Solution 2
![]()
![]()
![]()
![]() vladimir.shelomovskii@gmail.com, vvsss
vladimir.shelomovskii@gmail.com, vvsss
Video Solution
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
See also
| 2024 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 7 |
Followed by Problem 9 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.