Difference between revisions of "DVI exam"
(→2022 221 problem 7) |
(→2022 222 problem 7) |
||
| Line 23: | Line 23: | ||
==2022 222 problem 7== | ==2022 222 problem 7== | ||
[[File:MSU 2022 2 7.png|400px|right]] | [[File:MSU 2022 2 7.png|400px|right]] | ||
| − | < | + | A sphere of diameter <math>1</math> is inscribed in a pyramid at the base of which lies a rhombus with an acute angle <math>2\alpha</math> and side <math>\sqrt{6}.</math> Find the angle <math>2\alpha</math> if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of <math>60^\circ.</math> |
| − | <cmath>AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},</cmath> | + | |
| − | <cmath>AM + BM = AB \implies</cmath> | + | <i><b>Solution 1</b></i> |
| + | |||
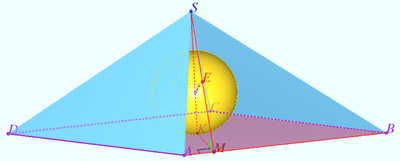
| + | Denote rhombus <math>ABCD, K = AC \cap BD, S</math> is the vertex of a pyramid <math>SK \perp ABC, I</math> is the center of the sphere, <math>IK = r = \frac {1}{2}, M \in AB, SM \perp AB, E</math> is the tangent point of <math>SM</math> and sphere, <math>\angle SMK = 60 ^\circ.</math> | ||
| + | <cmath>IE = r, SK = SI + IK = \frac {3}{2}, KM = \frac {\sqrt{3}}{2}, SM = \sqrt{3}.</cmath> | ||
| + | <cmath>AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},</cmath> | ||
| + | <cmath>AM + BM = AB = \sqrt{6}\implies</cmath> | ||
<cmath>\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.</cmath> | <cmath>\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.</cmath> | ||
| + | <i><b>Solution 2</b></i> | ||
| + | |||
| + | The area of the rhombus <math>[ABCD]= AB^2 \cdot \sin 2\alpha.</math> | ||
| + | |||
| + | The area of the lateral surface is <math>[l]= 4 [SAB] = 2 \cdot AB \cdot SM.</math> | ||
| + | <cmath>[ABCD] = [l] \cdot \cos 60 ^\circ =[l] \cdot \frac{1}{2} \implies AB \cdot SM = AB^2 \cdot \sin 2\alpha \implies</cmath> | ||
| + | <cmath>\sin {2 \alpha} = \frac {SM}{AB} = \frac {\sqrt{3}}{\sqrt{6}} = \frac {1}{\sqrt{2}}.</cmath> | ||
| + | <i><b>Answer:<math> \frac {\pi}{4}.</math></b></i> | ||
Revision as of 06:15, 28 January 2024
2022 221 problem 7
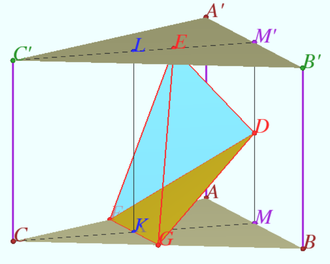
The volume of a triangular prism ![]() with base
with base ![]() and side edges
and side edges ![]() is equal to
is equal to ![]() Find the volume of the tetrahedron
Find the volume of the tetrahedron ![]() where
where ![]() is the centroid of the face
is the centroid of the face ![]() is the point of intersection of the medians of
is the point of intersection of the medians of ![]() is the midpoint of the edge
is the midpoint of the edge ![]() and
and ![]() is the midpoint of the edge
is the midpoint of the edge ![]()
Solution
Let us consider the uniform triangular prism ![]() Let
Let ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]() be the midpoint of
be the midpoint of ![]()
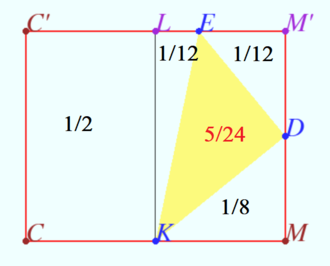
The area ![]() of
of ![]() in the sum with the areas of triangles
in the sum with the areas of triangles ![]() is half the area of rectangle
is half the area of rectangle ![]() so
so
![]()
![]() Denote the distance between these lines
Denote the distance between these lines ![]() The volume of the tetrahedron is
The volume of the tetrahedron is ![]()
![]() The volume of the prism is
The volume of the prism is ![]()
![]()
An arbitrary prism is obtained from a regular one as a result of an affine transformation.
All points on the tetrahedron are defined affinely, which means that the volume ratio will be preserved.
Answer: 5.
2022 222 problem 7
A sphere of diameter ![]() is inscribed in a pyramid at the base of which lies a rhombus with an acute angle
is inscribed in a pyramid at the base of which lies a rhombus with an acute angle ![]() and side
and side ![]() Find the angle
Find the angle ![]() if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of
if it is known that all lateral faces of the pyramid are inclined to plane of its base at an angle of ![]()
Solution 1
Denote rhombus ![]() is the vertex of a pyramid
is the vertex of a pyramid ![]() is the center of the sphere,
is the center of the sphere, ![]() is the tangent point of
is the tangent point of ![]() and sphere,
and sphere, ![]()
![]()
![]()
![]()
![]() Solution 2
Solution 2
The area of the rhombus ![]()
The area of the lateral surface is ![]()
![]()
![]() Answer:
Answer:![]()