Difference between revisions of "DVI exam"
(Created page with "==2022 222 problem 7== <cmath>r = 0.5, h = 3/2, KM = \frac {\sqrt{3}}{2},</cmath> <cmath>AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha} \implies AM + BM = AB</cmath>...") |
(→2022 222 problem 7) |
||
| Line 1: | Line 1: | ||
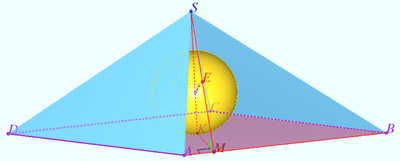
==2022 222 problem 7== | ==2022 222 problem 7== | ||
| + | [[File:MSU 2022 2 7.png|400px|right]] | ||
<cmath>r = 0.5, h = 3/2, KM = \frac {\sqrt{3}}{2},</cmath> | <cmath>r = 0.5, h = 3/2, KM = \frac {\sqrt{3}}{2},</cmath> | ||
| − | <cmath>AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha} | + | <cmath>AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},</cmath> |
| + | <cmath>AM + BM = AB \implies</cmath> | ||
<cmath>\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.</cmath> | <cmath>\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.</cmath> | ||
Revision as of 14:42, 27 January 2024
2022 222 problem 7
![\[r = 0.5, h = 3/2, KM = \frac {\sqrt{3}}{2},\]](http://latex.artofproblemsolving.com/1/d/c/1dca112ae88f73b3097142899ae597d9184f3a30.png)
![\[AM = KM \cdot \tan \alpha, BM = \frac {KM}{\tan \alpha},\]](http://latex.artofproblemsolving.com/2/b/c/2bc88738c2efa898feb0c22b93dc8754aa27f8d8.png)
![\[AM + BM = AB \implies\]](http://latex.artofproblemsolving.com/6/6/b/66bd3dd3f4588d2579c1569d2c36491417e20a8c.png)
![\[\tan \alpha + \frac {1}{\tan \alpha} = 2 \sqrt {2} \implies \tan \alpha = \sqrt {2} - 1 \implies \tan 2 \alpha = 1 \implies 2 \alpha = \frac {\pi}{4}.\]](http://latex.artofproblemsolving.com/a/d/9/ad94bbf8346d00722305ab7c3dca276520748cb6.png)
