Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1985 AJHSME Problem 24"

m (→‎Solution 2)
m (→‎Solution 2)
Line 36: Line 36:
 
Going clockwise around the circle and starting at the top, label the circles <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>f</math>. From the problem, we have that <math>a + b + c</math> = <math>c + d + e</math> = <math>e + f + a = S</math>, so <math>(a + b + c) + (c + d + e) + (e + f + a) = 2a + b + 2c + d + 2e + f = 3S</math>. The sum of <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>f</math> must be <math>75</math> (this is the sum of the possible values for the circles). From this, we have that <math>a + c + e + (a + b + c + d + e + f) = a + c + e + 75 = 3S</math>. To maximize <math>a + c + e</math>, we choose <math>a</math>, <math>c</math>, and <math>e</math> to be <math>15</math>, <math>14</math>, and <math>13</math> in some order (the choice is somewhat arbitrary due to the commutativity of addition). Then <math>(15 + 14 + 13) + 75 = 117 = 3S</math>, so <math>S = \boxed{39~\textbf{(D)}}</math>.
 
Going clockwise around the circle and starting at the top, label the circles <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>f</math>. From the problem, we have that <math>a + b + c</math> = <math>c + d + e</math> = <math>e + f + a = S</math>, so <math>(a + b + c) + (c + d + e) + (e + f + a) = 2a + b + 2c + d + 2e + f = 3S</math>. The sum of <math>a</math>, <math>b</math>, <math>c</math>, <math>d</math>, <math>e</math>, and <math>f</math> must be <math>75</math> (this is the sum of the possible values for the circles). From this, we have that <math>a + c + e + (a + b + c + d + e + f) = a + c + e + 75 = 3S</math>. To maximize <math>a + c + e</math>, we choose <math>a</math>, <math>c</math>, and <math>e</math> to be <math>15</math>, <math>14</math>, and <math>13</math> in some order (the choice is somewhat arbitrary due to the commutativity of addition). Then <math>(15 + 14 + 13) + 75 = 117 = 3S</math>, so <math>S = \boxed{39~\textbf{(D)}}</math>.
  
−
~ cxsmi
+
~ [https://artofproblemsolving.com/wiki/index.php/User:Cxsmi cxsmi]

Revision as of 12:42, 4 April 2024

Problem

In a magic triangle, each of the six whole numbers $10-15$ is placed in one of the circles so that the sum, $S$, of the three numbers on each side of the triangle is the same. The largest possible value for $S$ is

[asy] draw(circle((0,0),1)); draw(dir(60)--6*dir(60)); draw(circle(7*dir(60),1)); draw(8*dir(60)--13*dir(60)); draw(circle(14*dir(60),1)); draw((1,0)--(6,0)); draw(circle((7,0),1)); draw((8,0)--(13,0)); draw(circle((14,0),1)); draw(circle((10.5,6.0621778264910705273460621952706),1)); draw((13.5,0.86602540378443864676372317075294)--(11,5.1961524227066318805823390245176)); draw((10,6.9282032302755091741097853660235)--(7.5,11.258330249197702407928401219788)); [/asy]

$\text{(A)}\ 36 \qquad \text{(B)}\ 37 \qquad \text{(C)}\ 38 \qquad \text{(D)}\ 39 \qquad \text{(E)}\ 40$

Solution 1

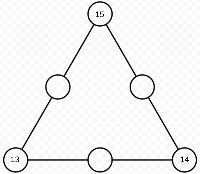
A numeral can appear in a maximum of 2 sides in this triangle, so we can put the largest 3 numbers, 15, 14, and 13 at the corners, as shown in Figure 1.

24 fig1.png Figure 1

Then, we can label the left empty circle as $a$ and the right empty circle as $a-1,$ because 14 is one more than 13, and we need to balance it out for the sum to be the same. The bottom empty circle can be named as $a+1$ because $13+14=15+13-1.$ We only can use the numbers $10, 11,$ and $12$ now, so $a=11,$ $a+1=12,$ and $a-1=10.$ Therefore, the largest value for $S$ is $15+11+13=10\cdot3+(5+3+1)=\boxed{39~\textbf{(D)}}.$

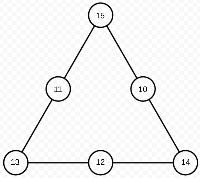
But, we have to make sure that all three sides sum to 39. The completed triangle is shown in Figure 2.

24 fig2.png Figure 2

Solution 2

Going clockwise around the circle and starting at the top, label the circles $a$, $b$, $c$, $d$, $e$, and $f$. From the problem, we have that $a + b + c$ = $c + d + e$ = $e + f + a = S$, so $(a + b + c) + (c + d + e) + (e + f + a) = 2a + b + 2c + d + 2e + f = 3S$. The sum of $a$, $b$, $c$, $d$, $e$, and $f$ must be $75$ (this is the sum of the possible values for the circles). From this, we have that $a + c + e + (a + b + c + d + e + f) = a + c + e + 75 = 3S$. To maximize $a + c + e$, we choose $a$, $c$, and $e$ to be $15$, $14$, and $13$ in some order (the choice is somewhat arbitrary due to the commutativity of addition). Then $(15 + 14 + 13) + 75 = 117 = 3S$, so $S = \boxed{39~\textbf{(D)}}$.

~ cxsmi

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1985_AJHSME_Problem_24&oldid=217810"