Difference between revisions of "1992 AIME Problems/Problem 10"
(category) |
|||
| Line 20: | Line 20: | ||
[[Category:Intermediate Algebra Problems]] | [[Category:Intermediate Algebra Problems]] | ||
[[Category:Intermediate Geometry Problems]] | [[Category:Intermediate Geometry Problems]] | ||
| + | {{MAA Notice}} | ||
Revision as of 18:24, 4 July 2013
Problem
Consider the region ![]() in the complex plane that consists of all points
in the complex plane that consists of all points ![]() such that both
such that both ![]() and
and ![]() have real and imaginary parts between
have real and imaginary parts between ![]() and
and ![]() , inclusive. What is the integer that is nearest the area of
, inclusive. What is the integer that is nearest the area of ![]() ?
?
Solution
Let ![]() . Since
. Since ![]() we have the inequality
we have the inequality ![]() which is a square of side length
which is a square of side length ![]() .
.
Also, ![]() so we have
so we have ![]() , which leads to:
, which leads to:![]()
![]()
We graph them:
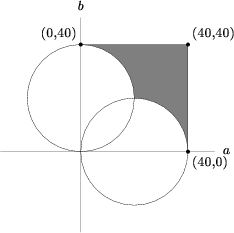
We want the area outside the two circles but inside the square. Doing a little geometry, the area of the intersection of those three graphs is ![]()
![]()
See also
| 1992 AIME (Problems • Answer Key • Resources) | ||
| Preceded by Problem 9 |
Followed by Problem 11 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 









