Difference between revisions of "2002 AIME I Problems/Problem 2"
m (→See also) |
|||
| Line 5: | Line 5: | ||
== Solution == | == Solution == | ||
| − | {{ | + | Let the radius of the circles is <math>r</math>. The longer dimension can be written as <math>14r</math>, and by Pythagorean Theorem, we can find that the shorter dimension: <math>2r\sqrt{3}+2r</math>. |
| + | |||
| + | Therefore, <math>\frac{14r}{2r\sqrt{3}+2r}=\frac{1}{2}(\sqrt{p}-q)</math> | ||
| + | |||
| + | After simplifying, we get <math>7\sqrt{3}-7=\sqrt{p}-q</math>, which gives <math>p=147</math> and <math>q=7</math>. So, <math>p+q=154</math> | ||
== See also == | == See also == | ||
{{AIME box|year=2002|n=I|num-b=1|num-a=3}} | {{AIME box|year=2002|n=I|num-b=1|num-a=3}} | ||
Revision as of 01:23, 29 December 2007
Problem
The diagram shows twenty congruent circles arranged in three rows and enclosed in a rectangle. The circles are tangent to one another and to the sides of the rectangle as shown in the diagram. The ratio of the longer dimension of the rectangle to the shorter dimension can be written as ![]() where
where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
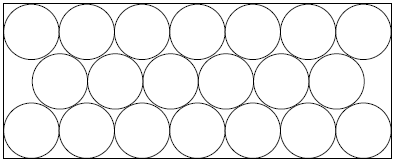
Solution
Let the radius of the circles is ![]() . The longer dimension can be written as
. The longer dimension can be written as ![]() , and by Pythagorean Theorem, we can find that the shorter dimension:
, and by Pythagorean Theorem, we can find that the shorter dimension: ![]() .
.
Therefore, ![]()
After simplifying, we get ![]() , which gives
, which gives ![]() and
and ![]() . So,
. So, ![]()
See also
| 2002 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 1 |
Followed by Problem 3 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||









