Difference between revisions of "2013 AIME II Problems/Problem 13"

Revision as of 00:23, 23 September 2023

Problem 13

In $\triangle ABC$ , $AC = BC$ , and point $D$ is on $\overline{BC}$ so that $CD = 3\cdot BD$ . Let $E$ be the midpoint of $\overline{AD}$ . Given that $CE = \sqrt{7}$ and $BE = 3$ , the area of $\triangle ABC$ can be expressed in the form $m\sqrt{n}$ , where $m$ and $n$ are positive integers and $n$ is not divisible by the square of any prime. Find $m+n$ .

Video Solution by Punxsutawney Phil

https://www.youtube.com/watch?v=IXPT0vHgt_c

Solution 1

We can set $AE=ED=m$ . Set $BD=k$ , therefore $CD=3k, AC=4k$ . Thereafter, by Stewart's Theorem on $\triangle ACD$ and cevian $CE$ , we get $2m^2+14=25k^2$ . Also apply Stewart's Theorem on $\triangle CEB$ with cevian $DE$ . After simplification, $2m^2=17-6k^2$ . Therefore, $k=1, m=\frac{\sqrt{22}}{2}$ . Finally, note that (using [] for area) $[CED]=[CAE]=3[EDB]=3[AEB]=\frac{3}{8}[ABC]$ , because of base-ratios. Using Heron's Formula on $\triangle EDB$ , as it is simplest, we see that $[ABC]=3\sqrt{7}$ , so your answer is $10$ .

Solution 2

After drawing the figure, we suppose $BD=a$ , so that $CD=3a$ , $AC=4a$ , and $AE=ED=b$ .

Using Law of Cosines for $\triangle AEC$ and $\triangle CED$ ,we get

$b^2+7-2\sqrt{7}\cdot \cos(\angle CED)=9a^2\qquad (1)$ $b^2+7+2\sqrt{7}\cdot \cos(\angle CED)=16a^2\qquad (2)$ So, $(1)+(2)$ , we get $2b^2+14=25a^2. \qquad (3)$

Using Law of Cosines in $\triangle ACD$ , we get

$b^2+9a^2-2\cdot 2b\cdot 3a\cdot \cos(\angle ADC)=16a^2$

So, $\cos(\angle ADC)=\frac{7a^2-4b^2}{12ab}.\qquad (4)$

Using Law of Cosines in $\triangle EDC$ and $\triangle EDB$ , we get

$b^2+9a^2-2\cdot 3a\cdot b\cdot \cos(\angle ADC)=7\qquad (5)$

$b^2+a^2+2\cdot a\cdot b\cdot \cos(\angle ADC)=9.\qquad (6)$

$(5)+(6)$ , and according to $(4)$ , we can get $37a^2+2b^2=48. \qquad (7)$

Using $(3)$ and $(7)$ , we can solve $a=1$ and $b=\frac{\sqrt{22}}{2}$ .

Finally, we use Law of Cosines for $\triangle ADB$ ,

$4(\frac{\sqrt{22}}{2})^2+1+2\cdot2(\frac{\sqrt{22}}{2})\cdot \cos(ADC)=AB^2$

then $AB=2\sqrt{7}$ , so the height of this $\triangle ABC$ is $\sqrt{4^2-(\sqrt{7})^2}=3$ .

Then the area of $\triangle ABC$ is $3\sqrt{7}$ , so the answer is $\boxed{010}$ .

Solution 3

Let $X$ be the foot of the altitude from $C$ with other points labelled as shown below. $[asy] size(200); pair A=(0,0),B=(2*sqrt(7),0),C=(sqrt(7),3),D=(3*B+C)/4,L=C/5,M=3*B/7; draw(A--B--C--cycle);draw(A--D^^B--L^^C--M); label("$A$",A,SW);label("$B$",B,SE);label("$C$",C,N);label("$D$",D,NE);label("$L$",L,NW);label("$M$",M,S); pair X=foot(C,A,B), Y=foot(L,A,B); pair EE=D/2; label("$X$",X,S);label("$E$",EE,NW);label("$Y$",Y,S); draw(C--X^^L--Y,dotted); draw(rightanglemark(B,X,C)^^rightanglemark(B,Y,L)); [/asy]$ Now we proceed using mass points. To balance along the segment $BC$ , we assign $B$ a mass of $3$ and $C$ a mass of $1$ . Therefore, $D$ has a mass of $4$ . As $E$ is the midpoint of $AD$ , we must assign $A$ a mass of $4$ as well. This gives $L$ a mass of $5$ and $M$ a mass of $7$ .

Now let $AB=b$ be the base of the triangle, and let $CX=h$ be the height. Then as $AM:MB=3:4$ , and as $AX=\frac{b}{2}$ , we know that $MX=\frac{b}{2}-\frac{3b}{7}=\frac{b}{14}.$ Also, as $CE:EM=7:1$ , we know that $EM=\frac{1}{\sqrt{7}}$ . Therefore, by the Pythagorean Theorem on $\triangle {XCM}$ , we know that $\frac{b^2}{196}+h^2=\left(\sqrt{7}+\frac{1}{\sqrt{7}}\right)^2=\frac{64}{7}.$

Also, as $LE:BE=5:3$ , we know that $BL=\frac{8}{5}\cdot 3=\frac{24}{5}$ . Furthermore, as $\triangle YLA\sim \triangle XCA$ , and as $AL:LC=1:4$ , we know that $LY=\frac{h}{5}$ and $AY=\frac{b}{10}$ , so $YB=\frac{9b}{10}$ . Therefore, by the Pythagorean Theorem on $\triangle BLY$ , we get $\frac{81b^2}{100}+\frac{h^2}{25}=\frac{576}{25}.$ Solving this system of equations yields $b=2\sqrt{7}$ and $h=3$ . Therefore, the area of the triangle is $3\sqrt{7}$ , giving us an answer of $\boxed{010}$ .

Solution 4

Let the coordinates of A, B and C be (-a, 0), (a, 0) and (0, h) respectively. Then $D = (\frac{3a}{4}, \frac{h}{4})$ and $E = (-\frac{a}{8},\frac{h}{8}).$ $EC^2 = 7$ implies $a^2 + 49h^2 = 448$ ; $EB^2 = 9$ implies $81a^2 + h^2 = 576.$ Solve this system of equations simultaneously, $a=\sqrt{7}$ and $h=3$ . Area of the triangle is ah = $3\sqrt{7}$ , giving us an answer of $\boxed{010}$ .

Solution 5

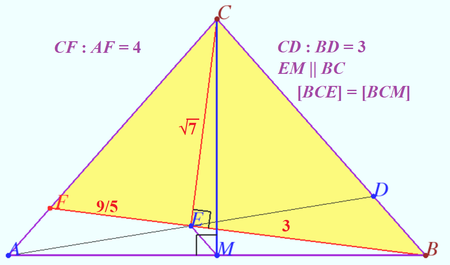
$[asy] size(200); pair A=(0,0),B=(2*sqrt(7),0),C=(sqrt(7),3),D=(3*B+C)/4,L=C/5,M=3*B/7; draw(A--B--C--cycle);draw(A--D^^B--L^^C--M); label("$A$",A,SW);label("$B$",B,SE);label("$C$",C,N);label("$D$",D,NE);label("$L$",L,NW);label("$M$",M,S); pair EE=D/2; label("$\sqrt{7}$", C--EE, W); label("$x$", D--B, E); label("$3x$", C--D, E); label("$l$", EE--D, N); label("$3$", EE--B, N); label("$E$",EE,NW); [/asy]$

Let $BD = x$ . Then $CD = 3x$ and $AC = 4x$ . Also, let $AE = ED = l$ . Using Stewart's Theorem on $\bigtriangleup CEB$ gives us the equation $(x)(3x)(4x) + (4x)(l^2) = 27x + 7x$ or, after simplifying, $4l^2 = 34 - 12x^2$ . We use Stewart's again on $\bigtriangleup CAD$ : $(l)(l)(2l) + 7(2l) = (16x^2)(l) + (9x^2)(l)$ , which becomes $2l^2 = 25x^2 - 14$ . Substituting $2l^2 = 17 - 6x^2$ , we see that $31x^2 = 31$ , or $x = 1$ . Then $l^2 = \frac{11}{2}$ .

We now use Law of Cosines on $\bigtriangleup CAD$ . $(2l)^2 = (4x)^2 + (3x)^2 - 2(4x)(3x)\cos C$ . Plugging in for $x$ and $l$ , $22 = 16 + 9 - 2(4)(3)\cos C$ , so $\cos C = \frac{1}{8}$ . Using the Pythagorean trig identity $\sin^2 + \cos^2 = 1$ , $\sin^2 C = 1 - \frac{1}{64}$ , so $\sin C = \frac{3\sqrt{7}}{8}$ .

$[ABC] = \frac{1}{2} AC \cdot BC \sin C = (\frac{1}{2})(4)(4)(\frac{3\sqrt{7}}{8}) = 3\sqrt{7}$ , and our answer is $3 + 7 = \boxed{010}$ .

Note to writter: Couldn't we just use Heron's formula for $[CEB]$ after $x$ is solved then noticing that $[ABC] = 2 \times [CEB]$ ?

Solution 6 (Barycentric Coordinates)

Let ABC be the reference triangle, with $A=(1,0,0)$ , $B=(0,1,0)$ , and $C=(0,0,1)$ . We can easily calculate $D=(0,\frac{3}{4},\frac{1}{4})$ and subsequently $E=(\frac{1}{2},\frac{3}{8},\frac{1}{8})$ . Using distance formula on $\overline{EC}=(\frac{1}{2},\frac{3}{8},-\frac{7}{8})$ and $\overline{EB}=(\frac{1}{2},-\frac{5}{8},\frac{1}{8})$ gives

$\begin{align*} \begin{cases} 7&=|EC|^2=-a^2 \cdot \frac{3}{8} \cdot (-\frac{7}{8})-b^2 \cdot \frac{1}{2} \cdot (-\frac{7}{8})-c^2 \cdot \frac{1}{2} \cdot \frac{3}{8} \\ 9&=|EB|^2=-a^2 \cdot (-\frac{5}{8}) \cdot \frac{1}{8}-b^2 \cdot \frac{1}{2} \cdot \frac{1}{8}-c^2 \cdot \frac{1}{2} \cdot (-\frac{5}{8}) \\ \end{cases} \end{align*}$

But we know that $a=b$ , so we can substitute and now we have two equations and two variables. So we can clear the denominators and prepare to cancel a variable:

$\begin{align*} \begin{cases} 7\cdot 64&=3\cdot 7\cdot a^2+b^2\cdot 4\cdot 7-c^2\cdot 4\cdot 3\\ 9\cdot 64&=5a^2-4b^2+4\cdot 5\cdot c^2 \\ \end{cases} \end{align*}$

$\begin{align*} \begin{cases} 7\cdot 64&=49a^2-12c^2 \\ 9\cdot 64&=a^2+20c^2 \\ \end{cases} \end{align*}$

$\begin{align*} \begin{cases} 5\cdot 7\cdot 64&=245a^2-60c^2 \\ 3\cdot 9\cdot 64&=3a^2+60c^2 \\ \end{cases} \end{align*}$

Then we add the equations to get

$\begin{align*} 62\cdot 64&=248a^2 \\ a^2 &=16 \\ a &=4 \\ \end{align*}$

Then plugging gives $b=4$ and $c=2\sqrt{7}$ . Then the height from $C$ is $3$ , and the area is $3\sqrt{7}$ and our answer is $\boxed{010}$ .

Solution 7

Let $C=(0,0), A=(x,y),$ and $B=(-x,y)$ . It is trivial to show that $D=\left(-\frac{3}{4}x,\frac{3}{4}y\right)$ and $E=\left(\frac{1}{8}x,\frac{7}{8}y\right)$ . Thus, since $BE=3$ and $CE=\sqrt{7}$ , we get that

$\begin{align*} \left(\frac{1}{8}x\right)^2+\left(\frac{7}{8}y\right)^2&=7 \\ \left(\frac{9}{8}x\right)^2+\left(\frac{1}{8}y\right)^2&=9 \\ \end{align*}$

Multiplying both equations by $64$ , we get that

$\begin{align*} x^2+49y^2&=448 \\ 81x^2+y^2&=576 \\ \end{align*}$

Solving these equations, we get that $x=\sqrt{7}$ and $y=3$ .

Thus, the area of $\triangle ABC$ is $xy=3\sqrt{7}$ , so our answer is $\boxed{010}$ .

Solution 8

The main in solution is to prove that $\angle BEC = 90^\circ$ .

Let $M$ be midpoint $AB.$ Let $F$ be cross point of $AC$ and $BE.$

We use the formula for crossing segments in $\triangle ABC$ and get: $\frac {CF}{AF}= \frac {DE}{AE} \cdot (\frac {CD}{BD} + 1) = 1 \cdot (3 + 1) = 4.$ $\frac {FE }{BE}= \frac {CD}{BD} : (\frac {CF}{AF} + 1) = \frac {3}{5} \implies FE = \frac {9}{5}.$

$\triangle BCF:\hspace{5mm} BC = x, CF = \frac {4}{5}x, EF = \frac {9}{5}, BF = 3, CE = \sqrt{7}.$ By Stewart's Theorem on $\triangle BCF$ and cevian $CE$ , we get after simplification $x = 4 \implies BC^2 = CE^2 + BE^2 \implies \angle BEC = 90^\circ.$ $AE = ED, AM = MB \implies EM ||BC.$ $\angle BEC = \angle CMB = 90^\circ \implies$ trapezium $BCEM$ is cyclic $\implies$ $BM = CE, CM = BE \implies [ABC] = CM \cdot BM = 3 \sqrt {7} \implies 3+ 7 = \boxed{\textbf{010}}.$ vladimir.shelomovskii@gmail.com, vvsss

2013 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search