Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Barycentric coordinates"

(→‎Useful formulas)
(→‎Useful formulas)
Line 10: Line 10:
  
 
==Useful formulas==
 
==Useful formulas==
 +
<i><b>Notation</b></i>
 +
 
Let the triangle <math>\triangle ABC</math> be a given triangle, <math>a, b, c</math> be the lengths of <math>BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.</math>
 
Let the triangle <math>\triangle ABC</math> be a given triangle, <math>a, b, c</math> be the lengths of <math>BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.</math>
  
Line 18: Line 20:
 
<math>r^2 = \frac {(s-a)(s-b)(s-c)}{s},</math> where <math>r</math> is the inradius, <math>R = \frac {abc}{2 \cdot 2S}</math> is the circumradius,
 
<math>r^2 = \frac {(s-a)(s-b)(s-c)}{s},</math> where <math>r</math> is the inradius, <math>R = \frac {abc}{2 \cdot 2S}</math> is the circumradius,
  
−
<math>\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}</math> is the cosine of the Brocard angle.
+
<math>\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}</math> is the cosine of the Brocard angle,
 +
 
 +
<cmath>S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.</cmath>
 +
 
 +
<i><b>Main</b></i>
  
−
<cmath>S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.</cmath>
+
For any point in the plane  <math>ABC</math> there are <i><b>barycentric coordinates(BC):</b></i> <math>\vec X = (x : y: z)</math>:
−
For any point in the plane  <math>ABC</math> there are barycentric coordinates:
 
 
<cmath>x \cdot \vec {XA} + y \cdot \vec {YB} + z \cdot \vec {XC} = \vec {0},</cmath>
 
<cmath>x \cdot \vec {XA} + y \cdot \vec {YB} + z \cdot \vec {XC} = \vec {0},</cmath>
 
<cmath>\vec X = \frac {x \cdot \vec {A} + y \cdot \vec {B} + z \cdot \vec {C}}{x+y+z}.</cmath>  
 
<cmath>\vec X = \frac {x \cdot \vec {A} + y \cdot \vec {B} + z \cdot \vec {C}}{x+y+z}.</cmath>  
−
The normalized (absolute) barycentric coordinates NBC satisfy the condition <math>x + y + z = 1,</math> they are uniquely determined:
+
The <i><b>normalized (absolute)</b></i> barycentric coordinates <i><b>NBC</b></i> satisfy the condition <math>x + y + z = 1,</math> they are uniquely determined:
 
<cmath>x = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z = \frac{[\vec {XA},\vec {XB}]}{\sigma},  \sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .</cmath>
 
<cmath>x = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z = \frac{[\vec {XA},\vec {XB}]}{\sigma},  \sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .</cmath>
 
Triangle vertices <math>A = (1:0:0), B = (0:1:0), C = (0:0:1).</math>
 
Triangle vertices <math>A = (1:0:0), B = (0:1:0), C = (0:0:1).</math>
  
−
The barycentric coordinates of a point do not change under an affine transformation.
+
The barycentric coordinates of a point <i><b> do not change </b></i> under an affine transformation.
 +
 
 +
<i><b>Lines</b></i>
  
 
The straight line in barycentric coordinates (BC) is given by the equation <math>kx + ly + mz = 0.</math>
 
The straight line in barycentric coordinates (BC) is given by the equation <math>kx + ly + mz = 0.</math>
Line 39: Line 46:
 
The sideline <math>BC</math> contains the points <math>B = (0:1:0), C = (0:0:1),</math> its equation is <math>x = 0.</math>
 
The sideline <math>BC</math> contains the points <math>B = (0:1:0), C = (0:0:1),</math> its equation is <math>x = 0.</math>
  
−
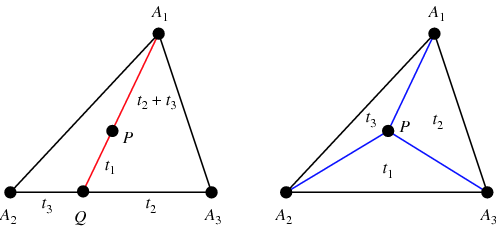
The line <math>AX, X = (k_1 :  l_1  :  m_1)</math> has equation <math>l_1z = m_1 y,</math> it intersects the sideline <math>BC</math> at the point <math>A_1 = (0 : l_1 : m_1), \frac {BA_1}{A_1C} = \frac {m_1}{l_1}.</math>
+
The line <math>AX, X = (k_1 :  l_1  :  m_1)</math> has equation <math>l_1z = m_1 y,</math> it intersects the sideline <math>BC</math> at the point <math>A_X = (0 : l_1 : m_1), \frac {BA_X}{A_XC} = \frac {m_1}{l_1}, \frac {AX}{XA_X} = \frac {m_1 + l_1}{k_1}.</math>
  
−
Iff <math>A_1 = (0 : l_1 : m_1), B_1 = (k_1  : 0 : m_1 ), C_1 = (k_1  : l_1  : 0),</math> then <math>AA_1 \cap BB_1 \cap CC_1 = (k_1  : l_1 : m_1 ).</math>
+
Iff <math>A_X = (0 : l_1 : m_1), B_X = (k_1  : 0 : m_1 ), C_X = (k_1  : l_1  : 0),</math> then <math>AA_X \cap BB_X \cap CC_X = (k_1  : l_1 : m_1 ).</math>
  
 
Let NBC of points <math>P</math> and <math>Q</math> be <math>P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).</math>
 
Let NBC of points <math>P</math> and <math>Q</math> be <math>P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).</math>
Line 49: Line 56:
 
The equation of bisector of <math>PQ</math> is:
 
The equation of bisector of <math>PQ</math> is:
 
<cmath>x(c^2(y_2-y_1) + b^2(z_2-z_1)) + y(a^2(z_2-z_1) + c^2(x_2-x_1)) + z(a^2(y_2-y_1) + b^2(x_2-x_1)) + a^2(y_1z_1 - y_2z_2) + b^2(x_1z_1-x_2z_2) + c^2 (x_1y_1 – x_2y_2).</cmath>
 
<cmath>x(c^2(y_2-y_1) + b^2(z_2-z_1)) + y(a^2(z_2-z_1) + c^2(x_2-x_1)) + z(a^2(y_2-y_1) + b^2(x_2-x_1)) + a^2(y_1z_1 - y_2z_2) + b^2(x_1z_1-x_2z_2) + c^2 (x_1y_1 – x_2y_2).</cmath>
 +
Nagel line : <math> (b-c) x + (c-a) y + (a-b) z = 0.</math>
  
 
<i><b>Circles</b></i>
 
<i><b>Circles</b></i>
Line 56: Line 64:
 
Circumcircle contains the points <math>A = (1:0:0), B = (0:1:0), C = (0:0:1) \implies</math>  
 
Circumcircle contains the points <math>A = (1:0:0), B = (0:1:0), C = (0:0:1) \implies</math>  
 
the equation of this circle:  <cmath>xyc^2 + xzb^2 + yza^2.</cmath>
 
the equation of this circle:  <cmath>xyc^2 + xzb^2 + yza^2.</cmath>
−
 
−
The circumcenter <math>O</math> lies at the intersection of the bisectors <math>AB (c^2(x - y) + z(a^2 – b^2) =0)</math> and <math>AC (b^2(x - z) + y(a^2 – c^2) =0) \implies</math> its BC coordinates <math>O = (a^2S_A : b^2S_B : c^2S_C).</math>
 
  
 
The incircle contains the tangent points of the incircle with the sides:
 
The incircle contains the tangent points of the incircle with the sides:
 
<cmath>\left(0 : \frac {a+b-c}{2a} : \frac {a-b+c}{2a}\right), \left(\frac {a+b-c}{2b} : 0 : \frac {-a+b+c}{2b}\right), \left(\frac {a-b+c}{2c} : \frac {-a+b+c}{2c}\right).</cmath>
 
<cmath>\left(0 : \frac {a+b-c}{2a} : \frac {a-b+c}{2a}\right), \left(\frac {a+b-c}{2b} : 0 : \frac {-a+b+c}{2b}\right), \left(\frac {a-b+c}{2c} : \frac {-a+b+c}{2c}\right).</cmath>
  
−
The incenter is <math>I = (a : b: c).</math> The equation of the incircle is  
+
The equation of the incircle is  
 
<cmath>{k_a}^2x^2 + k_b^2y^2 + k_c^2z^2 - 2k_a k_b  xy - 2k_a k_c xz - 2k_bk_cyz = 0,</cmath> where <math>k_a = b+c - a, k_b = a+c - b, k_c = a + b - c.</math>  
 
<cmath>{k_a}^2x^2 + k_b^2y^2 + k_c^2z^2 - 2k_a k_b  xy - 2k_a k_c xz - 2k_bk_cyz = 0,</cmath> where <math>k_a = b+c - a, k_b = a+c - b, k_c = a + b - c.</math>  
  
−
The excenters are <math>I_A = (-a : b : c), I_B =(a : -b: c), I_C = (a : b : -c).</math>
+
 
  
 
The radical axis of two circles given by equations of this form is:
 
The radical axis of two circles given by equations of this form is:
 
<cmath>k_1xa + l_1yb + m_1zc = k_2xa + l_2yb + m_2zc.</cmath>
 
<cmath>k_1xa + l_1yb + m_1zc = k_2xa + l_2yb + m_2zc.</cmath>
 +
<i><b>Conjugate</b></i>
  
 
The point <math>P = (x : y : z)</math> is isotomically conjugate with respect to <math>\triangle ABC</math> with the point <math>P_1 =\left( \frac {1}{x} :  \frac {1}{y} :  \frac {1}{z}\right).</math>
 
The point <math>P = (x : y : z)</math> is isotomically conjugate with respect to <math>\triangle ABC</math> with the point <math>P_1 =\left( \frac {1}{x} :  \frac {1}{y} :  \frac {1}{z}\right).</math>
Line 77: Line 84:
 
<i><b>Triangle centers</b></i>
 
<i><b>Triangle centers</b></i>
  
−
Centroid <math>G = (1 : 1 : 1).</math>
+
The median <math>AA_G, A_G \in BC \implies \frac {BA_G}{CA_G} = 1 \implies</math> <i><b>centroid</b></i> is  <math>G = (1 : 1 : 1).</math>  
−
   
+
 
 +
The simmedian point <math>K</math> is  isogonally conjugate with respect to <math>\triangle ABC</math>  with the point <math>G \implies K =  \left( a^2 :  b^2 : c^2\right).</math>
 +
 
 +
The bisector <math>AA_I, A_I \in BC \implies \frac {BA_I}{CA_I} = \frac {c}{b} \implies</math> the incenter is <math>I = (a : b: c).</math>
 +
 
 +
The excenters are <math>I_A = (-a : b : c), I_B =(a : -b: c), I_C = (a : b : -c).</math>
 +
 
 +
The circumcenter <math>O</math> lies at the intersection of the bisectors <math>AB (c^2(x - y) + z(a^2 – b^2) =0)</math> and <math>AC (b^2(x - z) + y(a^2 – c^2) =0) \implies</math> its BC coordinates <math>O = (a^2S_A : b^2S_B : c^2S_C).</math>
 +
 
 
The orthocenter <math>H</math> is  isogonally conjugate with respect to <math>\triangle ABC</math> with the point <math>O \implies H =\left( \frac {1}{S_A} :  \frac {1}{S_B} :  \frac {1}{S_C}\right).</math>
 
The orthocenter <math>H</math> is  isogonally conjugate with respect to <math>\triangle ABC</math> with the point <math>O \implies H =\left( \frac {1}{S_A} :  \frac {1}{S_B} :  \frac {1}{S_C}\right).</math>
  
Line 84: Line 99:
 
   
 
   
 
The Gergonne point is the isotomic conjugate of the Nagel point, so <math>Ge=\left( \frac {1}{b+c-a} : \frac{1}{a+c-b} : \frac{1}{a+b-c}\right ).</math>
 
The Gergonne point is the isotomic conjugate of the Nagel point, so <math>Ge=\left( \frac {1}{b+c-a} : \frac{1}{a+c-b} : \frac{1}{a+b-c}\right ).</math>
 +
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''

Revision as of 03:31, 26 August 2023

This can be used in mass points. http://mathworld.wolfram.com/BarycentricCoordinates.html This article is a stub. Help us out by expanding it.

Barycentric coordinates are triples of numbers $(t_1,t_2,t_3)$ corresponding to masses placed at the vertices of a reference triangle $\Delta{A_1}{A_2}{A_3}$. These masses then determine a point $P$, which is the geometric centroid of the three masses and is identified with coordinates $(t_1,t_2,t_3)$. The vertices of the triangle are given by $(1,0,0)$, $(0,1,0)$, and $(0,0,1)$. Barycentric coordinates were discovered by Möbius in 1827 (Coxeter 1969, p. 217; Fauvel et al. 1993).

The Central NC Math Group published a lecture concerning this topic at https://www.youtube.com/watch?v=KQim7-wrwL0 if you would like to view it.

Barycentric 901.gif

Useful formulas

Notation

Let the triangle $\triangle ABC$ be a given triangle, $a, b, c$ be the lengths of $BC, AC, AB, \angle A = \alpha, \angle B = \beta, \angle C = \gamma.$

We use the following Conway symbols:

$s = \frac {a+b+c}{2}$ is semiperimeter, $2S$ is twice the area of $\triangle ABC,$

$r^2 = \frac {(s-a)(s-b)(s-c)}{s},$ where $r$ is the inradius, $R = \frac {abc}{2 \cdot 2S}$ is the circumradius,

$\cos \omega = \frac {a^2 + b^2 +c^2}{2 \cdot 2S}$ is the cosine of the Brocard angle,

\[S_A = bc \cos \alpha = \frac{b^2+c^2-a^2}{2}, S_B = ac \cos \beta =\frac{a^2 +c^2-b^2}{2}, S_C = ab \cos \gamma = \frac {a^2+b^2-c^2}{2}.\]

Main

For any point in the plane $ABC$ there are barycentric coordinates(BC): $\vec X = (x : y: z)$: \[x \cdot \vec {XA} + y \cdot \vec {YB} + z \cdot \vec {XC} = \vec {0},\] \[\vec X = \frac {x \cdot \vec {A} + y \cdot \vec {B} + z \cdot \vec {C}}{x+y+z}.\] The normalized (absolute) barycentric coordinates NBC satisfy the condition $x + y + z = 1,$ they are uniquely determined: \[x = \frac{[\vec {XB},\vec {XC}]}{\sigma}, y = \frac{[\vec {XC},\vec {XA}]}{\sigma}, z = \frac{[\vec {XA},\vec {XB}]}{\sigma}, \sigma = [\vec {XB},\vec {XC}] + [\vec {XC},\vec {XA}] + [\vec {XA},\vec {XB}] .\] Triangle vertices $A = (1:0:0), B = (0:1:0), C = (0:0:1).$

The barycentric coordinates of a point do not change under an affine transformation.

Lines

The straight line in barycentric coordinates (BC) is given by the equation $kx + ly + mz = 0.$

The lines given in the BC by the equations $k_1x + l_1y + m_1z = 0$ and $k_2x + l_2y + m_2z = 0$ intersect at the point \[(l_1m_2 – m_1l_2 : m_1k_2-k_1m_2 : k_1l_2-l_1k_2).\]

These lines are parallel iff $l_1m_2 – m_1l_2 + m_1k_2-k_1m_2 + k_1l_2-l_1k_2 = 0.$

The sideline $BC$ contains the points $B = (0:1:0), C = (0:0:1),$ its equation is $x = 0.$

The line $AX, X = (k_1 : l_1  : m_1)$ has equation $l_1z = m_1 y,$ it intersects the sideline $BC$ at the point $A_X = (0 : l_1 : m_1), \frac {BA_X}{A_XC} = \frac {m_1}{l_1}, \frac {AX}{XA_X} = \frac {m_1 + l_1}{k_1}.$

Iff $A_X = (0 : l_1 : m_1), B_X = (k_1  : 0 : m_1 ), C_X = (k_1  : l_1  : 0),$ then $AA_X \cap BB_X \cap CC_X = (k_1  : l_1 : m_1 ).$

Let NBC of points $P$ and $Q$ be $P = (x_1 : y_1 : z_1), Q = (x_2 : y_2 : z_2).$

Then the square of distance \[|PQ|^2 = S_A \cdot (x_1 - x_2)^2 + S_B(y_1 - y_2)^2 + S_C(z_1 - z_2)^2.\] \[|PQ|^2 = - a^2 (y_1 - y_2)(z_1 - z_2) - b^2 (x_1 - x_2)(z_1 - z_2) - c^2 (x_1 - x_2)(y_1 - y_2).\] The equation of bisector of $PQ$ is: \[x(c^2(y_2-y_1) + b^2(z_2-z_1)) + y(a^2(z_2-z_1) + c^2(x_2-x_1)) + z(a^2(y_2-y_1) + b^2(x_2-x_1)) + a^2(y_1z_1 - y_2z_2) + b^2(x_1z_1-x_2z_2) + c^2 (x_1y_1 – x_2y_2).\] Nagel line : $(b-c) x + (c-a) y + (a-b) z = 0.$

Circles

Any circle is given by an equation of the form $(kx + ly + mz)(x +y + z) = xyc^2 + xzb^2 + yza^2.$

Circumcircle contains the points $A = (1:0:0), B = (0:1:0), C = (0:0:1) \implies$ the equation of this circle: \[xyc^2 + xzb^2 + yza^2.\]

The incircle contains the tangent points of the incircle with the sides: \[\left(0 : \frac {a+b-c}{2a} : \frac {a-b+c}{2a}\right), \left(\frac {a+b-c}{2b} : 0 : \frac {-a+b+c}{2b}\right), \left(\frac {a-b+c}{2c} : \frac {-a+b+c}{2c}\right).\]

The equation of the incircle is \[{k_a}^2x^2 + k_b^2y^2 + k_c^2z^2 - 2k_a k_b xy - 2k_a k_c xz - 2k_bk_cyz = 0,\] where $k_a = b+c - a, k_b = a+c - b, k_c = a + b - c.$


The radical axis of two circles given by equations of this form is: \[k_1xa + l_1yb + m_1zc = k_2xa + l_2yb + m_2zc.\] Conjugate

The point $P = (x : y : z)$ is isotomically conjugate with respect to $\triangle ABC$ with the point $P_1 =\left( \frac {1}{x} : \frac {1}{y} : \frac {1}{z}\right).$

The point $P = (x : y : z)$ is isogonally conjugate with respect to $\triangle ABC$ with the point $P_2 =\left( \frac {a^2}{x} : \frac {b^2}{y} : \frac {c^2}{z}\right).$

Triangle centers

The median $AA_G, A_G \in BC \implies \frac {BA_G}{CA_G} = 1 \implies$ centroid is $G = (1 : 1 : 1).$

The simmedian point $K$ is isogonally conjugate with respect to $\triangle ABC$ with the point $G \implies K = \left( a^2 : b^2 : c^2\right).$

The bisector $AA_I, A_I \in BC \implies \frac {BA_I}{CA_I} = \frac {c}{b} \implies$ the incenter is $I = (a : b: c).$

The excenters are $I_A = (-a : b : c), I_B =(a : -b: c), I_C = (a : b : -c).$

The circumcenter $O$ lies at the intersection of the bisectors $AB (c^2(x - y) + z(a^2 – b^2) =0)$ and $AC (b^2(x - z) + y(a^2 – c^2) =0) \implies$ its BC coordinates $O = (a^2S_A : b^2S_B : c^2S_C).$

The orthocenter $H$ is isogonally conjugate with respect to $\triangle ABC$ with the point $O \implies H =\left( \frac {1}{S_A} : \frac {1}{S_B} : \frac {1}{S_C}\right).$

Let Nagel point $N$ lies at line $AA_N, A_N \in BC \implies \frac {BA_N}{A_NC} = \frac {a+c-b}{a+b-c} \implies N=(b+c-a: a+c-b:a+b-c).$

The Gergonne point is the isotomic conjugate of the Nagel point, so $Ge=\left( \frac {1}{b+c-a} : \frac{1}{a+c-b} : \frac{1}{a+b-c}\right ).$

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Barycentric_coordinates&oldid=197489"