Difference between revisions of "2023 AIME II Problems/Problem 6"
(→See also) |
(→Solution 3 (Geometry)) |
||
| Line 96: | Line 96: | ||
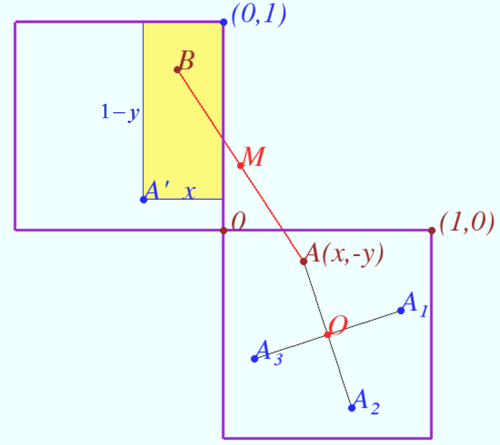
We use the coordinate system shown in diagram. Let the arbitrary point <math>A(x, -y), x \in [0,1], y \in [0,1]</math> be in right square. | We use the coordinate system shown in diagram. Let the arbitrary point <math>A(x, -y), x \in [0,1], y \in [0,1]</math> be in right square. | ||
| − | It is clear that iff point <math>B</math> lies in yellow rectangle with sides <math>x</math> and <math>1 – y,</math> then the midpoint <math>AB</math> lies outside of the <math>L.</math> Probability of this is <math>p = x(1 – y).</math> | + | It is clear that iff point <math>B</math> lies in yellow rectangle with sides <math>x</math> and <math>1 – y,</math> then the midpoint <math>AB</math> lies outside of the <math>L.</math> |
| − | Consider the points <math>A_1(y,x | + | |
| − | The probability that the midpoint of one of the segments <math>A_1B, A_2B, A_3B</math> and <math>AB</math> is outside of the <math>L</math> shape is < | + | Probability of this is <math>p = x(1 – y).</math> |
| − | If point <math>A</math> is in the right square | + | |
| + | Consider the points <math>A_1(1-y,-x), A_2(1-x,y-1), A_3(y,x-1).</math> | ||
| + | |||
| + | Similarly we find <math>p_1 = (1-y)(1-x), p_2= (1-x)y, p_3 = xy.</math> | ||
| + | |||
| + | The probability that the midpoint of one of the segments <math>A_1B, A_2B, A_3B</math> and <math>AB</math> is outside of the <math>L-</math>shape is <cmath>\frac {p_1+p_2+p_3+p}{4} = \frac {1}{4}.</cmath> | ||
| + | If point <math>A</math> is in the right square, point <math>B</math> in the top square, the probability that the midpoint of <math>\overline{AB}</math> lies outside <math>L-</math>shape is <math>\frac {1}{4} \implies </math> | ||
| + | |||
| + | If points <math>A</math> and <math>B</math> are chosen independently and uniformly at random in <math>L-</math>shape, then the probability that the midpoint of <math>\overline{AB}</math> lies outside <math>L-</math>shape is <math>\frac {1}{4} \cdot \frac {2}{9} = \frac {1}{18}.</math> | ||
Therefore the probability that the point is inside the <math>L-</math>shape is <math>1-\frac{1}{18}=\frac{17}{18} \implies \boxed{35}.</math> | Therefore the probability that the point is inside the <math>L-</math>shape is <math>1-\frac{1}{18}=\frac{17}{18} \implies \boxed{35}.</math> | ||
Revision as of 09:26, 6 March 2023
Contents
Problem
Consider the L-shaped region formed by three unit squares joined at their sides, as shown below. Two points ![]() and
and ![]() are chosen independently and uniformly at random from inside the region. The probability that the midpoint of
are chosen independently and uniformly at random from inside the region. The probability that the midpoint of ![]() also lies inside this L-shaped region can be expressed as
also lies inside this L-shaped region can be expressed as ![]() where
where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]()
![[asy] unitsize(2cm); draw((0,0)--(2,0)--(2,1)--(1,1)--(1,2)--(0,2)--cycle); draw((0,1)--(1,1)--(1,0),dashed); [/asy]](http://latex.artofproblemsolving.com/3/5/e/35e5685ec38ac2940e2bd21b651c8faa1f022f57.png)
Video Solution by MOP 2024
https://youtube.com/watch?v=0UViBt-LYTo&t=0s
Solution 1
We proceed by calculating the complement.
Note that the only configuration of the 2 points that makes the midpoint outside of the L shape is one point in the top square, and one in the right square. This occurs with ![]() probability.
probability.
Let the topmost coordinate have value of: ![]() , and rightmost value of:
, and rightmost value of: ![]() .
.
The midpoint of them is thus: ![]()
It is clear that ![]() are all between 0 and 1. For the midpoint to be outside the L-shape, both coordinates must be greater than 1, thus:
are all between 0 and 1. For the midpoint to be outside the L-shape, both coordinates must be greater than 1, thus:
![]()
![]()
By symmetry this has probability ![]() . Also by symmetry, the probability the y-coordinate works as well is
. Also by symmetry, the probability the y-coordinate works as well is ![]() . Thus the probability that the midpoint is outside the L-shape is:
. Thus the probability that the midpoint is outside the L-shape is:
![]()
![]()
We want the probability that the point is inside the L-shape however, which is ![]() , yielding the answer of
, yielding the answer of ![]() ~SAHANWIJETUNGA
~SAHANWIJETUNGA
Solution 2(Calculus)
We assume each box has side length 1.
We index the upper left box, the bottom left box, the bottom right box as II, III, IV, respectively.
We index the missing upper right box as I.
We put the graph to a coordinate system by putting the intersecting point of four foxes at the origin, the positive direction of the ![]() axis at the intersecting line of boxes I and IV, and the positive direction of the
axis at the intersecting line of boxes I and IV, and the positive direction of the ![]() -axis at the intersecting line of boxes I and II.
We denote by
-axis at the intersecting line of boxes I and II.
We denote by ![]() the midpoint of
the midpoint of ![]() .
.
Therefore,
![]()
We observe that a necessary for ![]() is either
is either ![]() and
and ![]() , or
, or ![]() and
and ![]() .
In addition, by symmetry,
.
In addition, by symmetry,
![]()
Thus,
 The second equality follows from the condition that the positions of
The second equality follows from the condition that the positions of ![]() and
and ![]() are independent.
The sixth equality follows from the condition that for each point of
are independent.
The sixth equality follows from the condition that for each point of ![]() and
and ![]() , the
, the ![]() and
and ![]() coordinate are independent.
coordinate are independent.
Therefore,

Therefore, the answer is ![]() .
.
~Steven Chen (Professor Chen Education Palace, www.professorchenedu.com)
Solution 3 (Geometry)
The only configuration of two points that makes the midpoint outside of the ![]() shape is one point in the top square, and one in the right square with probability
shape is one point in the top square, and one in the right square with probability ![]() (see Solution
(see Solution ![]()
We use the coordinate system shown in diagram. Let the arbitrary point ![]() be in right square.
It is clear that iff point
be in right square.
It is clear that iff point ![]() lies in yellow rectangle with sides
lies in yellow rectangle with sides ![]() and
and ![]() then the midpoint
then the midpoint ![]() lies outside of the
lies outside of the ![]()
Probability of this is ![]()
Consider the points ![]()
Similarly we find ![]()
The probability that the midpoint of one of the segments ![]() and
and ![]() is outside of the
is outside of the ![]() shape is
shape is ![]() If point
If point ![]() is in the right square, point
is in the right square, point ![]() in the top square, the probability that the midpoint of
in the top square, the probability that the midpoint of ![]() lies outside
lies outside ![]() shape is
shape is ![]()
If points ![]() and
and ![]() are chosen independently and uniformly at random in
are chosen independently and uniformly at random in ![]() shape, then the probability that the midpoint of
shape, then the probability that the midpoint of ![]() lies outside
lies outside ![]() shape is
shape is ![]() Therefore the probability that the point is inside the
Therefore the probability that the point is inside the ![]() shape is
shape is ![]()
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2023 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.