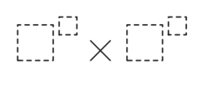Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2023 AMC 8 Problems/Problem 6"

(→‎Solution 2)
Line 15: Line 15:
  
 
~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing))
 
~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing))
 +
 +
==Video Solution by Magic Square==
 +
https://youtu.be/-N46BeEKaCQ?t=5247
  
 
==See Also==  
 
==See Also==  
 
{{AMC8 box|year=2023|num-b=5|num-a=7}}
 
{{AMC8 box|year=2023|num-b=5|num-a=7}}
 
{{MAA Notice}}
 
{{MAA Notice}}

Revision as of 10:48, 25 January 2023

Problem

The digits 2, 0, 2, and 3 are placed in the expression below, one digit per box. What is the maximum possible value of the expression?

2023 AMC 8-6.png

$\textbf{(A) }0 \qquad \textbf{(B) }8 \qquad \textbf{(C) }9 \qquad \textbf{(D) }16 \qquad \textbf{(E) }18$

Solution 1

First, let us consider the cases where $0$ is a base. This would result in the entire expression being $0$. However, if $0$ is an exponent, we will get a value greater than $0$. As $3^2\cdot2^0=9$ is greater than $2^3\cdot2^0=8$ and $2^2\cdot3^0=4$, the answer is $\boxed{\textbf{(C) }9}$.

~MathFun1000

Solution 2

The maximum possible value of using the digit $2,0,2,3$. We can maximize our value by keeping the $3$ and $2$ together in one power. (Biggest with biggest and smallest with smallest) This shows $3^{2}*0^{2}$=$9*1$=$9$. (Don't want $2^{0}$ cause that's $0$) It is going to be $\boxed{\text{(C)}9}$

~apex304 (SohumUttamchandani, wuwang2002, TaeKim, Cxrupptedpat, stevens0209 (editing))

Video Solution by Magic Square

https://youtu.be/-N46BeEKaCQ?t=5247

See Also

2023 AMC 8 (Problems • Answer Key • Resources)
Preceded by
Problem 5 		Followed by
Problem 7
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AJHSME/AMC 8 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2023_AMC_8_Problems/Problem_6&oldid=187882"