Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "Simson line"

(→‎Simson line of a complete quadrilateral)
(→‎Simson line of a complete quadrilateral)
Line 45: Line 45:
 
==Simson line of a complete quadrilateral==
 
==Simson line of a complete quadrilateral==
 
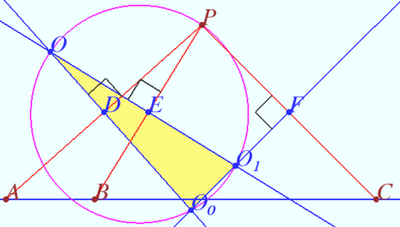
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>  
 
Let four lines made four triangles of a complete quadrilateral. In the diagram these are <math>\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.</math>  
−
Let <math>M</math> be the Miquel point of a complete quadrilateral. Let <math>D, E, F,</math> and <math>G</math> be the foots of the perpendiculars dropped from <math>M</math> to lines <math>AB, AC, BC,</math> and EF, respectively.  
+
Let <math>M</math> be the Miquel point of a complete quadrilateral. Let <math>K, L, N,</math> and <math>G</math> be the foots of the perpendiculars dropped from <math>M</math> to lines <math>AB, AC, EF,</math> and <math>BC,</math> respectively.
 +
 +
Prove that points <math>K,L, N,</math> and <math>G</math> are collinear.  
  
−
Prove that points <math>D, E, F,</math> and <math>G</math> are collinear.
+
<i><b>Proof</b></i>
  
 +
Let <math>\Omega</math> be the circumcircle of <math>\triangle ABC, \omega</math> be the circumcircle of <math>\triangle CEF.</math> Then <math>M = \Omega \cap \omega.</math>
 +
 +
Points <math>K, L,</math> and <math>G</math> are collinear as Simson line of <math>\triangle ABC.</math>
 +
 +
Points <math>L, N,</math> and <math>G</math> are collinear as Simson line of <math>\triangle CEF.</math>
 +
 +
Therefore points <math>K, L, N,</math> and <math>G</math> are collinear, as desired.
 +
*[[Miquel point]]
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
  
 
<i><b>Proof</b></i>
 
<i><b>Proof</b></i>

Revision as of 12:58, 7 December 2022

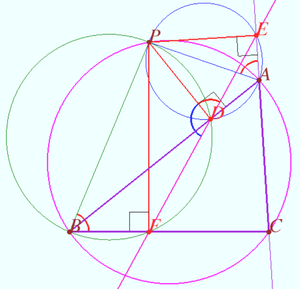
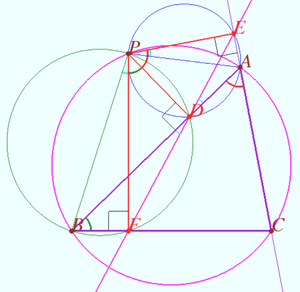
In geometry, given a triangle ABC and a point P on its circumcircle, the three closest points to P on lines AB, AC, and BC are collinear. Simsonline.png

Simson line (main)

Simson line.png
Simson line inverse.png

Let a triangle $\triangle ABC$ and a point $P$ be given.

Let $D, E,$ and $F$ be the foots of the perpendiculars dropped from P to lines AB, AC, and BC, respectively.

Then points $D, E,$ and $F$ are collinear iff the point $P$ lies on circumcircle of $\triangle ABC.$

Proof

Let the point $P$ be on the circumcircle of $\triangle ABC.$

$\angle BFP = \angle BDP = 90^\circ \implies$

$BPDF$ is cyclic $\implies \angle PDF = 180^\circ – \angle CBP.$

$\angle ADP = \angle AEP = 90^\circ \implies$

$AEPD$ is cyclic $\implies \angle PDE = \angle PAE.$

$ACBP$ is cyclic $\implies \angle PBC = \angle PAE \implies \angle PDF + \angle PDE = 180^\circ$

$\implies D, E,$ and $F$ are collinear as desired.

Proof

Let the points $D, E,$ and $F$ be collinear.

$AEPD$ is cyclic $\implies \angle APE = \angle ADE, \angle APE = \angle BAC.$

$BFDP$ is cyclic $\implies \angle BPF = \angle BDF, \angle DPF = \angle ABC.$

$\angle ADE = \angle BDF \implies \angle BPA = \angle EPF$

$= \angle BAC + \angle ABC = 180^\circ – \angle ACB \implies$

$ACBP$ is cyclis as desired.

vladimir.shelomovskii@gmail.com, vvsss

Simson line of a complete quadrilateral

Let four lines made four triangles of a complete quadrilateral. In the diagram these are $\triangle ABC, \triangle ADE, \triangle CEF, \triangle BDF.$ Let $M$ be the Miquel point of a complete quadrilateral. Let $K, L, N,$ and $G$ be the foots of the perpendiculars dropped from $M$ to lines $AB, AC, EF,$ and $BC,$ respectively.

Prove that points $K,L, N,$ and $G$ are collinear.

Proof

Let $\Omega$ be the circumcircle of $\triangle ABC, \omega$ be the circumcircle of $\triangle CEF.$ Then $M = \Omega \cap \omega.$

Points $K, L,$ and $G$ are collinear as Simson line of $\triangle ABC.$

Points $L, N,$ and $G$ are collinear as Simson line of $\triangle CEF.$

Therefore points $K, L, N,$ and $G$ are collinear, as desired.

vladimir.shelomovskii@gmail.com, vvsss

Proof

vladimir.shelomovskii@gmail.com, vvsss

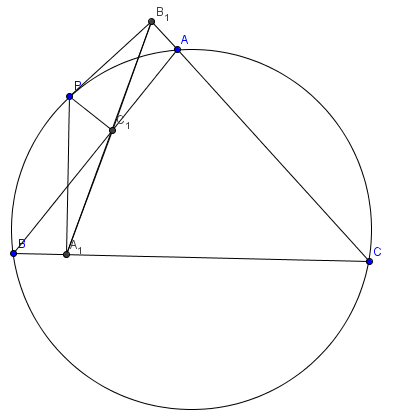
Problem

Problem on Simson line.png

Let the points $A, B,$ and $C$ be collinear and the point $P \notin AB.$

Let $O,O_0,$ and $O_1$ be the circumcenters of triangles $\triangle ABP, \triangle ACP,$ and $\triangle BCP.$

Prove that $P$ lies on circumcircle of $\triangle OO_0O_1.$

Proof

Let $D, E,$ and $F$ be the midpoints of segments $AB, AC,$ and $BC,$ respectively.

Then points $D, E,$ and $F$ are collinear $(DE||AB, EF||DC).$

$PD \perp OO_0, PE \perp OO_1, PF \perp O_0O_1 \implies$ $DEF$ is Simson line of $\triangle OO_0O_1 \implies P$ lies on circumcircle of $\triangle OO_0O_1$ as desired.

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=Simson_line&oldid=183708"