Difference between revisions of "Double perspective triangles"
(→Two triangles in double perspective are in triple perspective) |
(→Two triangles in double perspective are in triple perspective) |
||
| Line 11: | Line 11: | ||
It is known that there is projective transformation that maps any quadrungle into square. | It is known that there is projective transformation that maps any quadrungle into square. | ||
| − | We use this transformation for <math>BDFG</math>. We use the | + | We use this transformation for <math>BDFG</math>. |
| + | We use the <i><b>Claim for square</b></i> and get the result: lines <math>AE, BF,</math> and <math>CD</math> are concurrent. | ||
| + | |||
| + | <i><b>Claim for square</b></i> | ||
| + | Let <math>ADBG</math> be the square, let <math>CEGF</math> be the rectangle, <math>A \in FG, G \in BE.</math> | ||
| + | Prove that lines <math>BF, CD,</math> and <math>AE</math> are concurrent. | ||
| + | |||
| + | <i><b>Proof</b></i> | ||
| + | |||
| + | Let <math>BG = a, GE = b, AF = c, A = (0,0).</math> Then | ||
| + | <cmath>B=(− a, − a), F = (0,c), BF: y= x (1 + \frac {c}{a})+c.</cmath> | ||
| + | <cmath>E=(b, − a), AE: y = − \frac {a}{b}x.</cmath> | ||
| + | <cmath>D = (−a,0), C= (b,c), CD: y = c \frac {x+a}{a+b}.</cmath> | ||
| + | <math>X = CD \cap AE \cap BF = (− b, a) \frac {c}{a+b +{\frac {bc}{a}}</math> as desired. | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
Revision as of 13:41, 5 December 2022
Double perspective triangles
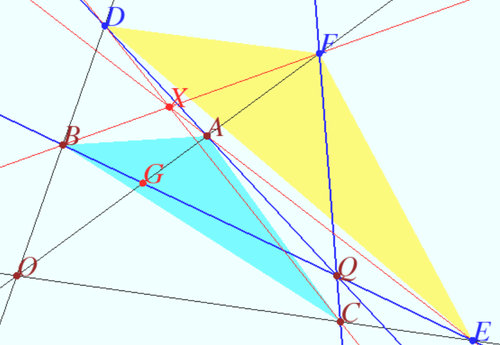
Two triangles in double perspective are in triple perspective
Let 
and 
be in double perspective, which means that triples of lines 
and 
are concurrent. Prove that lines 
and 
are concurrent (the triangles are in triple perspective).
Proof
Denote 
It is known that there is projective transformation that maps any quadrungle into square.
We use this transformation for 
.
We use the Claim for square and get the result: lines and are concurrent.
Claim for square
Let 
be the square, let 
be the rectangle, 
Prove that lines 
and 
are concurrent.
Proof
Let 
Then
\[B=(− a, − a), F = (0,c), BF: y= x (1 + \frac {c}{a})+c.\] (Error compiling LaTeX. Unknown error_msg)
\[E=(b, − a), AE: y = − \frac {a}{b}x.\] (Error compiling LaTeX. Unknown error_msg)
\[D = (−a,0), C= (b,c), CD: y = c \frac {x+a}{a+b}.\] (Error compiling LaTeX. Unknown error_msg)
$X = CD \cap AE \cap BF = (− b, a) \frac {c}{a+b +{\frac {bc}{a}}$ (Error compiling LaTeX. Unknown error_msg) as desired.
vladimir.shelomovskii@gmail.com, vvsss
