Difference between revisions of "Double perspective triangles"
(→Two triangles in double perspective are in triple perspective) |
|||
| Line 2: | Line 2: | ||
==Two triangles in double perspective are in triple perspective== | ==Two triangles in double perspective are in triple perspective== | ||
| − | + | [[File:Exeter B.png|500px|right]] | |
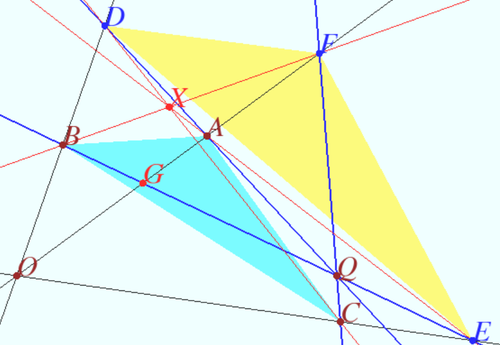
Let <math>\triangle ABC</math> and <math>\triangle DEF</math> be in double perspective, which means that triples of lines <math>AF, BD, CE</math> and <math>AD, BE, CF</math> are concurrent. Prove that lines <math>AE, BF,</math> and <math>CD</math> are concurrent (the triangles are in triple perspective). | Let <math>\triangle ABC</math> and <math>\triangle DEF</math> be in double perspective, which means that triples of lines <math>AF, BD, CE</math> and <math>AD, BE, CF</math> are concurrent. Prove that lines <math>AE, BF,</math> and <math>CD</math> are concurrent (the triangles are in triple perspective). | ||
| Line 9: | Line 9: | ||
Denote <math>G = AF \cap BE.</math> | Denote <math>G = AF \cap BE.</math> | ||
| − | It is known that there is projective transformation that maps any quadrungle into square. We use this transformation for <math>BDFG</math>. We use the claim and get the result: lines <math>AE, BF,</math> and <math>CD</math> are concurrent. | + | It is known that there is projective transformation that maps any quadrungle into square. |
| + | |||
| + | We use this transformation for <math>BDFG</math>. We use the claim and get the result: lines <math>AE, BF,</math> and <math>CD</math> are concurrent. | ||
Revision as of 13:35, 5 December 2022
Double perspective triangles
Two triangles in double perspective are in triple perspective
Let ![]() and
and ![]() be in double perspective, which means that triples of lines
be in double perspective, which means that triples of lines ![]() and
and ![]() are concurrent. Prove that lines
are concurrent. Prove that lines ![]() and
and ![]() are concurrent (the triangles are in triple perspective).
are concurrent (the triangles are in triple perspective).
Proof
Denote ![]()
It is known that there is projective transformation that maps any quadrungle into square.
We use this transformation for ![]() . We use the claim and get the result: lines
. We use the claim and get the result: lines ![]() and
and ![]() are concurrent.
are concurrent.