Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1983 AIME Problems/Problem 15"

(→‎Solution)
(image)
Line 1: Line 1:
 
== Problem ==
 
== Problem ==
−
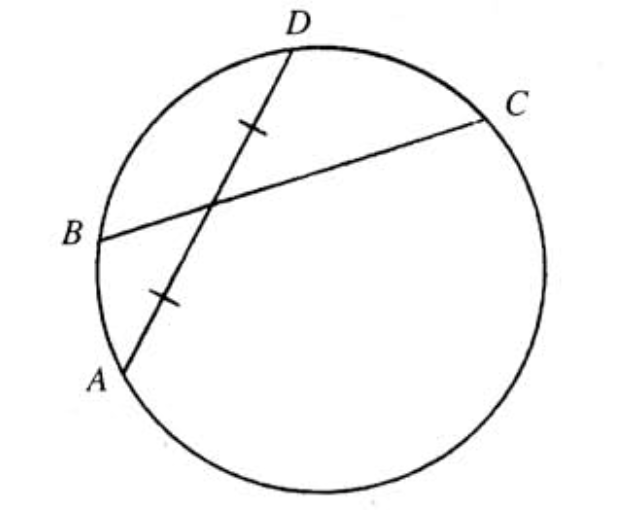
The adjoining figure shows two intersecting chords in a circle, with <math>B</math> on minor arc <math>AD</math>. Suppose that the radius of the circle is <math>5</math>, that <math>BC=6</math>, and that <math>AD</math> is bisected by <math>BC</math>. Suppose further that <math>AD</math> is the only chord starting at <math>A</math> which is bisected by <math>BC</math>. It follows that the sine of the minor arc <math>AB</math> is a rational number. If this fraction is expressed as a fraction <math>\frac{m}{n}</math> in lowest terms, what is the product <math>mn</math>?
+
The adjoining figure shows two intersecting [[chord]]s in a [[circle]], with <math>B</math> on minor arc <math>AD</math>. Suppose that the radius of the circle is <math>5</math>, that <math>BC=6</math>, and that <math>AD</math> is [[bisect]]ed by <math>BC</math>. Suppose further that <math>AD</math> is the only chord starting at <math>A</math> which is bisected by <math>BC</math>. It follows that the [[sine]] of the minor arc <math>AB</math> is a rational number. If this fraction is expressed as a fraction <math>\frac{m}{n}</math> in lowest terms, what is the product <math>mn</math>?
  
−
[[Image:1983 AIME Problem 15.png]]
+
[[Image:1983_AIME-15.png]]
  
 
== Solution ==
 
== Solution ==
 
Let <math>A</math> be any [[fixed point]] on [[circle]] <math>O</math> and let <math>AD</math> be a [[chord]] of circle <math>O</math>. The [[locus]] of [[midpoint]]s <math>N</math> of the chord <math>AD</math> is a circle <math>P</math>, with diameter <math>AD</math>. Generally, the circle <math>P</math> can intersect the chord <math>BC</math> at two points, one point, or they may not have a point of intersection. By the problem condition, however, the circle <math>P</math> is tangent to BC at point N.  
 
Let <math>A</math> be any [[fixed point]] on [[circle]] <math>O</math> and let <math>AD</math> be a [[chord]] of circle <math>O</math>. The [[locus]] of [[midpoint]]s <math>N</math> of the chord <math>AD</math> is a circle <math>P</math>, with diameter <math>AD</math>. Generally, the circle <math>P</math> can intersect the chord <math>BC</math> at two points, one point, or they may not have a point of intersection. By the problem condition, however, the circle <math>P</math> is tangent to BC at point N.  
  
−
Let M be the midpoint of the chord <math>BC</math> such that <math>BC=3</math>. From right angle triangle <math>OMB</math>, <math>OM = \sqrt{OB^2 - BM^2} =4</math>. Thus, <math>\tan \angle BOM = \frac{BM}{OM} = \frac 3 4</math>.
+
Let M be the midpoint of the chord <math>BC</math> such that <math>BC=3</math>. From [[right triangle]] <math>OMB</math>, <math>OM = \sqrt{OB^2 - BM^2} =4</math>. Thus, <math>\tan \angle BOM = \frac{BM}{OM} = \frac 3 4</math>.
  
 
Notice that the distance <math>OM</math> equals <math>PN + PO \cos AOM = r(1 + \cos AOM)</math> (Where <math>r</math> is the radius of circle P). Evaluating this, <math>\cos \angle AOM = \frac{OM}{r} - 1 = \frac{2OM}{R} - 1 = \frac 8 5 - 1 = \frac 3 5</math>. From <math>\cos \angle AOM</math>, we see that <math>\tan \angle AOM =\frac{\sqrt{1 - \cos^2 \angle AOM}}{\cos \angle AOM} = \frac{\sqrt{5^2 - 3^2}}{3} = \frac 4 3</math>
 
Notice that the distance <math>OM</math> equals <math>PN + PO \cos AOM = r(1 + \cos AOM)</math> (Where <math>r</math> is the radius of circle P). Evaluating this, <math>\cos \angle AOM = \frac{OM}{r} - 1 = \frac{2OM}{R} - 1 = \frac 8 5 - 1 = \frac 3 5</math>. From <math>\cos \angle AOM</math>, we see that <math>\tan \angle AOM =\frac{\sqrt{1 - \cos^2 \angle AOM}}{\cos \angle AOM} = \frac{\sqrt{5^2 - 3^2}}{3} = \frac 4 3</math>
  
−
Next, notice that <math>\angle AOB = \angle AOM - \angle BOM</math>. We can therefore apply the tangent subtraction formula to obtain , <math>\tan AOB =\frac{\tan AOM - \tan BOM}{1 + \tan AOM \cdot \tan AOM} =\frac{\frac 4 3 - \frac 3 4}{1 + \frac 4 3 \cdot \frac 3 4} = \frac{7}{24}</math>. It follows that <math>\sin AOB =\frac{7}{\sqrt{7^2+24^2}} = \frac{7}{25}</math>, resulting in an answer of <math>7 \cdot 25=175</math>.
+
Next, notice that <math>\angle AOB = \angle AOM - \angle BOM</math>. We can therefore apply the tangent subtraction formula to obtain , <math>\tan AOB =\frac{\tan AOM - \tan BOM}{1 + \tan AOM \cdot \tan AOM} =\frac{\frac 4 3 - \frac 3 4}{1 + \frac 4 3 \cdot \frac 3 4} = \frac{7}{24}</math>. It follows that <math>\sin AOB =\frac{7}{\sqrt{7^2+24^2}} = \frac{7}{25}</math>, resulting in an answer of <math>7 \cdot 25=\boxed{175}</math>.
  
 
== See also ==
 
== See also ==
−
{{AIME box|year=1983|num-b=14|after=Last Question}}
+
{{AIME box|year=1983|num-b=14|after=Last question}}
−
* [[AIME Problems and Solutions]]
 
−
* [[American Invitational Mathematics Examination]]
 
−
* [[Mathematics competition resources]]
 
  
 
[[Category:Intermediate Geometry Problems]]
 
[[Category:Intermediate Geometry Problems]]

Revision as of 18:21, 25 April 2008

Problem

The adjoining figure shows two intersecting chords in a circle, with $B$ on minor arc $AD$. Suppose that the radius of the circle is $5$, that $BC=6$, and that $AD$ is bisected by $BC$. Suppose further that $AD$ is the only chord starting at $A$ which is bisected by $BC$. It follows that the sine of the minor arc $AB$ is a rational number. If this fraction is expressed as a fraction $\frac{m}{n}$ in lowest terms, what is the product $mn$?

1983 AIME-15.png

Solution

Let $A$ be any fixed point on circle $O$ and let $AD$ be a chord of circle $O$. The locus of midpoints $N$ of the chord $AD$ is a circle $P$, with diameter $AD$. Generally, the circle $P$ can intersect the chord $BC$ at two points, one point, or they may not have a point of intersection. By the problem condition, however, the circle $P$ is tangent to BC at point N.

Let M be the midpoint of the chord $BC$ such that $BC=3$. From right triangle $OMB$, $OM = \sqrt{OB^2 - BM^2} =4$. Thus, $\tan \angle BOM = \frac{BM}{OM} = \frac 3 4$.

Notice that the distance $OM$ equals $PN + PO \cos AOM = r(1 + \cos AOM)$ (Where $r$ is the radius of circle P). Evaluating this, $\cos \angle AOM = \frac{OM}{r} - 1 = \frac{2OM}{R} - 1 = \frac 8 5 - 1 = \frac 3 5$. From $\cos \angle AOM$, we see that $\tan \angle AOM =\frac{\sqrt{1 - \cos^2 \angle AOM}}{\cos \angle AOM} = \frac{\sqrt{5^2 - 3^2}}{3} = \frac 4 3$

Next, notice that $\angle AOB = \angle AOM - \angle BOM$. We can therefore apply the tangent subtraction formula to obtain , $\tan AOB =\frac{\tan AOM - \tan BOM}{1 + \tan AOM \cdot \tan AOM} =\frac{\frac 4 3 - \frac 3 4}{1 + \frac 4 3 \cdot \frac 3 4} = \frac{7}{24}$. It follows that $\sin AOB =\frac{7}{\sqrt{7^2+24^2}} = \frac{7}{25}$, resulting in an answer of $7 \cdot 25=\boxed{175}$.

See also

1983 AIME (Problems • Answer Key • Resources)
Preceded by
Problem 14 		Followed by
Last question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1983_AIME_Problems/Problem_15&oldid=25388"