Difference between revisions of "2016 USAMO Problems/Problem 3"
(→Solution 2) |
(→Solution 2) |
||
| Line 69: | Line 69: | ||
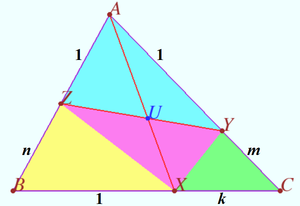
<cmath>\frac {AU}{UX} = \frac {[AYZ]}{[XYZ]} = \frac {m + nk}{k + 1}.</cmath> | <cmath>\frac {AU}{UX} = \frac {[AYZ]}{[XYZ]} = \frac {m + nk}{k + 1}.</cmath> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
'''vladimir.shelomovskii@gmail.com, vvsss''' | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==See also== | ==See also== | ||
{{USAMO newbox|year=2016|num-b=2|num-a=4}} | {{USAMO newbox|year=2016|num-b=2|num-a=4}} | ||
Revision as of 13:33, 12 October 2022
Contents
Problem
Let ![]() be an acute triangle, and let
be an acute triangle, and let ![]() and
and ![]() denote its
denote its ![]() -excenter,
-excenter, ![]() -excenter, and circumcenter, respectively. Points
-excenter, and circumcenter, respectively. Points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]() Similarly, points
Similarly, points ![]() and
and ![]() are selected on
are selected on ![]() such that
such that ![]() and
and ![]()
Lines ![]() and
and ![]() meet at
meet at ![]() Prove that
Prove that ![]() and
and ![]() are perpendicular.
are perpendicular.
Solution
This problem can be proved in the following two steps.
1. Let ![]() be the
be the ![]() -excenter, then
-excenter, then ![]() and
and ![]() are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for
are colinear. This can be proved by the Trigonometric Form of Ceva's Theorem for ![]()
2. Show that ![]() which implies
which implies ![]() This can be proved by multiple applications of the Pythagorean Thm.
This can be proved by multiple applications of the Pythagorean Thm.
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
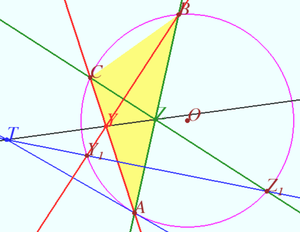
Solution 2
We find point ![]() on line
on line ![]() we prove that
we prove that ![]() and state that
and state that ![]() is the point
is the point ![]() from ENCYCLOPEDIA OF TRIANGLE, therefore
from ENCYCLOPEDIA OF TRIANGLE, therefore ![]()
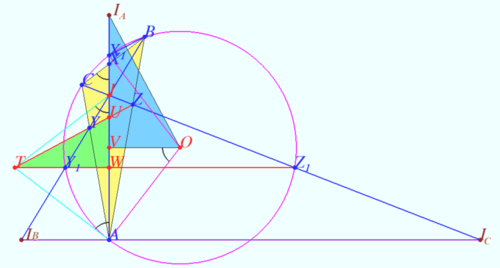
Let ![]() be circumcircle of
be circumcircle of ![]() centered at
centered at ![]() Let
Let ![]() and
and ![]() be crosspoints of
be crosspoints of ![]() and
and ![]() and
and ![]() respectively.
Let
respectively.
Let ![]() be crosspoint of
be crosspoint of ![]() and
and ![]() In accordance the Pascal theorem for pentagon
In accordance the Pascal theorem for pentagon ![]()
![]() is tangent to
is tangent to ![]() at
at ![]()
Let ![]() be
be ![]() and
and ![]() -excenters of
-excenters of ![]() Denote
Denote ![]()
![]()
![]()
![]() is the foot ot perpendicular from
is the foot ot perpendicular from ![]() to
to ![]()
![]() is ortocenter of
is ortocenter of ![]() and incenter of
and incenter of ![]()
![]() is the Nine–point circle of
is the Nine–point circle of ![]()
![]() is the midpoint of
is the midpoint of ![]() is the midpoint of
is the midpoint of ![]() in accordance with property of Nine–point circle
in accordance with property of Nine–point circle ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() In
In ![]() segment
segment ![]() cross segment
cross segment ![]() where
where ![]()
![]()
![]()
![]()
![]()
![]()
![]()
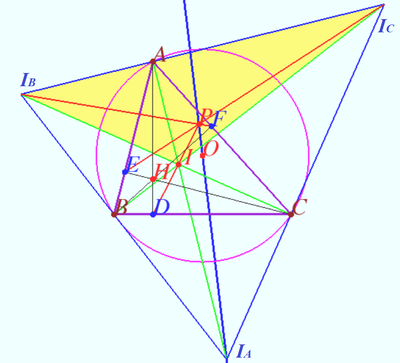
Let ![]() be the base triangle with orthocenter
be the base triangle with orthocenter ![]() center of Nine-points circle
center of Nine-points circle ![]() be the Euler line of
be the Euler line of ![]()
![]() is orthic triangle of
is orthic triangle of ![]()
![]() is orthic-of-orthic triangle.
is orthic-of-orthic triangle.
![]() is perspector of base triangle and orthic-of-orthic triangle.
is perspector of base triangle and orthic-of-orthic triangle.
Therefore ![]() is point
is point ![]() of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
[[1]]
of ENCYCLOPEDIA OF TRIANGLE CENTERS which lies on Euler line of the base triangle.
[[1]]
Claim ![]() Proof
Proof
![]()
![]()
![]()
![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See also
| 2016 USAMO (Problems • Resources) | ||
| Preceded by Problem 2 |
Followed by Problem 4 | |
| 1 • 2 • 3 • 4 • 5 • 6 | ||
| All USAMO Problems and Solutions | ||