Difference between revisions of "2017 USAMO Problems/Problem 3"
(→Solution) |
(→Solution) |
||
| Line 4: | Line 4: | ||
==Solution== | ==Solution== | ||
[[File:2017 USAMO 3.png|400px|right]] | [[File:2017 USAMO 3.png|400px|right]] | ||
| + | [[File:2017 USAMO 3a.png|400px|right]] | ||
Let <math>X</math> be the point on circle <math>\Omega</math> opposite <math>M \implies \angle MAX = 90^\circ, BC \perp XM.</math> | Let <math>X</math> be the point on circle <math>\Omega</math> opposite <math>M \implies \angle MAX = 90^\circ, BC \perp XM.</math> | ||
| Line 32: | Line 33: | ||
<math>\angle XI'I = \angle XAI = 90^\circ \implies</math> the points <math>X, I' ,</math> and <math>F</math> are collinear. | <math>\angle XI'I = \angle XAI = 90^\circ \implies</math> the points <math>X, I' ,</math> and <math>F</math> are collinear. | ||
| − | <math>I'IDD'</math> is cyclic <math>\implies \angle I'D'M = \angle I'D'C + 90^\circ = \angle I'ID + 90^\circ, \angle XFM = \angle I'FI = 90^\circ – \angle I'IF = 90^\circ – \angle I'ID \implies</math> | + | <math>I'IDD'</math> is cyclic <math>\implies \angle I'D'M = \angle I'D'C + 90^\circ = \angle I'ID + 90^\circ,</math> |
| + | <math>\angle XFM = \angle I'FI = 90^\circ – \angle I'IF = 90^\circ – \angle I'ID \implies</math> | ||
| − | <math>\angle XFM + \angle I'D'M = 180^\circ \implies I'D'MF</math> is cyclic. | + | <math>\angle XFM + \angle I'D'M = 180^\circ \implies I'D'MF</math> is cyclic. |
| + | |||
Therefore point <math>F</math> lies on <math>I_\omega (IDK).</math> | Therefore point <math>F</math> lies on <math>I_\omega (IDK).</math> | ||
| − | + | <math>FA \perp SX, SI' \perp FX \implies I</math> is orthocenter of <math>\triangle FSX.</math> | |
| − | <math>N</math> is midpoint <math>SI, M</math> is midpoint <math> | + | <math>N</math> is midpoint <math>SI, M</math> is midpoint <math>FI, I</math> is orthocenter of <math>\triangle FSX, A</math> is root of height <math>FA \implies AMN</math> is the nine-point circle of <math>\triangle FSX \implies I' \in AMN.</math> |
| − | Let <math>N' = I_\omega (N) \implies R^2 = SN \cdot SN' = SI \cdot SI' \implies \frac {SN'}{SI'} = \frac {SI}{SN} =2 \implies</ | + | Let <math>N' = I_\omega (N) \implies R^2 = SN \cdot SN' = SI \cdot SI' \implies</math> |
| + | <cmath>\frac {SN'}{SI'} = \frac {SI}{SN} =2 \implies</cmath> | ||
<math>\angle XN'I' = \angle XSI' = 90^\circ – \angle AXI' = \angle IFX \implies N'XIF</math> is cyclic. | <math>\angle XN'I' = \angle XSI' = 90^\circ – \angle AXI' = \angle IFX \implies N'XIF</math> is cyclic. | ||
Revision as of 04:38, 21 September 2022
Problem
Let ![]() be a scalene triangle with circumcircle
be a scalene triangle with circumcircle ![]() and incenter
and incenter ![]() Ray
Ray ![]() meets
meets ![]() at
at ![]() and
and ![]() again at
again at ![]() the circle with diameter
the circle with diameter ![]() cuts
cuts ![]() again at
again at ![]() Lines
Lines ![]() and
and ![]() meet at
meet at ![]() and
and ![]() is the midpoint of
is the midpoint of ![]() The circumcircles of
The circumcircles of ![]() and
and ![]() intersect at points
intersect at points ![]() and
and ![]() Prove that
Prove that ![]() passes through the midpoint of either
passes through the midpoint of either ![]() or
or ![]()
Solution
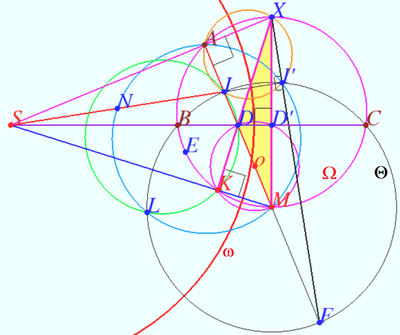
Let ![]() be the point on circle
be the point on circle ![]() opposite
opposite ![]()
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]()
![]() is the orthocenter of
is the orthocenter of ![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]() be the circle centered at
be the circle centered at ![]() with radius
with radius ![]()
We denote ![]() inversion with respect to
inversion with respect to ![]()
Note that the circle ![]() has diameter
has diameter ![]() and contain points
and contain points ![]() and
and ![]()
![]() circle
circle ![]()
![]() circle
circle ![]()
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Let ![]() It is well known that
It is well known that ![]()
![]() is circle centered at
is circle centered at ![]()
![]()
Let ![]()
![]() is cyclic.
is cyclic.
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
![]() is cyclic
is cyclic ![]()
![]()
![]() is cyclic.
is cyclic.
Therefore point ![]() lies on
lies on ![]()
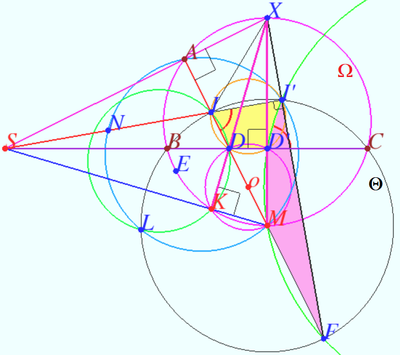
![]() is orthocenter of
is orthocenter of ![]()
![]() is midpoint
is midpoint ![]() is midpoint
is midpoint ![]() is orthocenter of
is orthocenter of ![]() is root of height
is root of height ![]() is the nine-point circle of
is the nine-point circle of ![]()
Let ![]()
![]()
![]() is cyclic.
is cyclic.
![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
Point ![]() is orthocenter
is orthocenter ![]() the points
the points ![]() and
and ![]() are collinear.
are collinear.
![]() is cyclic.
is cyclic.
Contact
Contact v_Enhance at https://www.facebook.com/v.Enhance.