Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2019 AIME II Problems/Problem 11"

(→‎Solution 7 (Heavy Bash))
(→‎Solution 7 (Heavy Bash))
Line 79: Line 79:
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
'''vladimir.shelomovskii@gmail.com, vvsss'''
 
== Solution 7 (Heavy Bash) ==
 
== Solution 7 (Heavy Bash) ==
−
We start by assigning coordinates to point <math>A, labeling it </math>(0,0)<math> and point </math>B at <math>(7,0)</math>, and letting point <math>C</math> be above the <math>x</math>-axis. Through an application of the Pythagorean Theorem and dropping an altitude to side <math>AB</math>, it is easy to see that <math>C</math> has coordinates <math>(33/7, 24\sqrt{5}/7)</math>.
+
We start by assigning coordinates to point <math>A</math>, labeling it <math>(0,0)</math> and point <math>B</math> at <math>(7,0)</math>, and letting point <math>C</math> be above the <math>x</math>-axis. Through an application of the Pythagorean Theorem and dropping an altitude to side <math>AB</math>, it is easy to see that <math>C</math> has coordinates <math>(33/7, 24\sqrt{5}/7)</math>.
 
   
 
   
 
Let <math>O1</math> be the center of circle <math>\omega_1</math>  and <math>O2</math> be the center of circle <math>\omega_2</math>. Since circle <math>\omega_1</math> contains both points <math>A</math> and <math>B</math>, <math>O1</math> must lie on the perpendicular bisector of line <math>AB</math>, and similarly <math>O2</math> must lie on the perpendicular bisector of line <math>AC</math>. Through some calculations, we find that the perpendicular bisector of <math>AB</math> has equation <math>x = 3.5</math>, and the perpendicular bisector of <math>AC</math> has equation <math>y = {-11\sqrt{5}/40 \cdot x} + 189\sqrt{5}/80</math>.  
 
Let <math>O1</math> be the center of circle <math>\omega_1</math>  and <math>O2</math> be the center of circle <math>\omega_2</math>. Since circle <math>\omega_1</math> contains both points <math>A</math> and <math>B</math>, <math>O1</math> must lie on the perpendicular bisector of line <math>AB</math>, and similarly <math>O2</math> must lie on the perpendicular bisector of line <math>AC</math>. Through some calculations, we find that the perpendicular bisector of <math>AB</math> has equation <math>x = 3.5</math>, and the perpendicular bisector of <math>AC</math> has equation <math>y = {-11\sqrt{5}/40 \cdot x} + 189\sqrt{5}/80</math>.  

Revision as of 23:44, 3 September 2022

Problem

Triangle $ABC$ has side lengths $AB=7, BC=8,$ and $CA=9.$ Circle $\omega_1$ passes through $B$ and is tangent to line $AC$ at $A.$ Circle $\omega_2$ passes through $C$ and is tangent to line $AB$ at $A.$ Let $K$ be the intersection of circles $\omega_1$ and $\omega_2$ not equal to $A.$ Then $AK=\tfrac mn,$ where $m$ and $n$ are relatively prime positive integers. Find $m+n.$

Solution 1

[asy] unitsize(20); pair B = (0,0); pair A = (2,sqrt(45)); pair C = (8,0); draw(circumcircle(A,B,(-17/8,0)),rgb(.7,.7,.7)); draw(circumcircle(A,C,(49/8,0)),rgb(.7,.7,.7)); draw(B--A--C--cycle); label("$A$",A,dir(105)); label("$B$",B,dir(-135)); label("$C$",C,dir(-75)); dot((2.68,2.25)); label("$K$",(2.68,2.25),dir(-150)); label("$\omega_1$",(-6,1)); label("$\omega_2$",(14,6)); label("$7$",(A+B)/2,dir(140)); label("$8$",(B+C)/2,dir(-90)); label("$9$",(A+C)/2,dir(60)); [/asy] -Diagram by Brendanb4321


Note that from the tangency condition that the supplement of $\angle CAB$ with respects to lines $AB$ and $AC$ are equal to $\angle AKB$ and $\angle AKC$, respectively, so from tangent-chord, \[\angle AKC=\angle AKB=180^{\circ}-\angle BAC\] Also note that $\angle ABK=\angle KAC$, so $\triangle AKB\sim \triangle CKA$. Using similarity ratios, we can easily find \[AK^2=BK*KC\] However, since $AB=7$ and $CA=9$, we can use similarity ratios to get \[BK=\frac{7}{9}AK, CK=\frac{9}{7}AK\]

  • Now we use Law of Cosines on $\triangle AKB$: From reverse Law of Cosines, $\cos{\angle BAC}=\frac{11}{21}\implies \cos{(180^{\circ}-\angle BAC)}=-\frac{11}{21}$. This gives us \[AK^2+\frac{49}{81}AK^2+\frac{22}{27}AK^2=49\] \[\implies \frac{196}{81}AK^2=49\] \[AK=\frac{9}{2}\] so our answer is $9+2=\boxed{011}$.

-franchester

  • The motivation for using the Law of Cosines ("LoC") is after finding the similar triangles it's hard to figure out what to do with $BK$ and $CK$ yet we know $BC$ which somehow has to help us solve the problem--a common theme in solving geometry problems is figuring out how to use what you haven't used yet. We know all three sides of some triangle though, and we're dealing with angles (that's how we found similarity), so why not try the Law of Cosines? This is to help with motivation--the solution is franchester's and I learned about using LoC from reading his solution (I only solved half the problem and got stuck). To anyone in the future reading this, math is beautiful.

-First

11111111:L)xiexie

Solution 2 (Inversion)

Consider an inversion with center $A$ and radius $r=AK$. Then, we have $AB\cdot AB^*=AK^2$, or $AB^*=\frac{AK^2}{7}$. Similarly, $AC^*=\frac{AK^2}{9}$. Notice that $AB^*KC^*$ is a parallelogram, since $\omega_1$ and $\omega_2$ are tangent to $AC$ and $AB$, respectively. Thus, $AC^*=B^*K$. Now, we get that \[\cos(\angle AB^*K)=-\cos(180-\angle BAC)=-\frac{11}{21}\] so by Law of Cosines on $\triangle AB^*K$ we have \[(AK)^2=(AB^*)2+(B^*K)^2-2\cdot AB^*\cdot B^*K \cdot \cos(\angle AB^*K)\] \[\Rightarrow (AK)^2=\frac{AK^4}{49}+\frac{AK^4}{81}-2\cdot \frac{AK^2}{7}\frac{AK^2}{9}\frac{-11}{21}\] \[\Rightarrow 1=\frac{AK^2}{49}+\frac{AK^2}{81}+\frac{22AK^2}{63\cdot21}\] \[\Rightarrow AK=\frac{9}{2}\] Then, our answer is $9+2=\boxed{11}$. -brianzjk

Solution 3 (Death By Trig Bash)

14. Let the centers of the circles be $O_{1}$ and $O_{2}$ where the $O_{1}$ has the side length $7$ contained in the circle. Now let $\angle BAC =x.$ This implies \[\angle AO_{1}B = \angle AO_{2}C = 2x\] by the angle by by tangent. Then we also know that \[\angle O_{1}AB = \angle O_{1}BA = \angle O_{2}AC = \angle O_{2}CA = 90^{\circ}-x\] Now we first find $\cos x.$ We use law of cosines on $\bigtriangleup ABC$ to obtain \[64 = 81 + 48 - 2 \cdot 9 \cdot 7 \cdot \cos{x}\] \[\implies \cos{x} =\frac{11}{21}\] \[\implies \sin{x} =\frac{8\sqrt{5}}{21}\] Then applying law of sines on $\bigtriangleup AO_{1}B$ we obtain \[\frac{7}{\sin{2x}} =\frac{OB_{1}}{\sin{90^{\circ}-x}}\] \[\implies\frac{7}{2\sin{x}\cos{x}} =\frac{OB_{1}}{\cos{x}}\] \[\implies OB_{1} = O_{1}A=\frac{147}{16\sqrt{5}}\] Using similar logic we obtain $OA_{1} =\frac{189}{16\sqrt{5}}.$

Now we know that $\angle O_{1}AO_{2}=180^{\circ}-x.$ Thus using law of cosines on $\bigtriangleup O_{1}AO_{2}$ yields \[O_{1}O_{2} =\sqrt{\left(\frac{147}{16\sqrt{5}}\right)^2+\left(\frac{189}{16\sqrt{5}}\right)^2-2\:\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot -\frac{11}{21}}\] While this does look daunting we can write the above expression as \[\sqrt{\left(\frac{189+147}{16\sqrt{5}}\right)^2 - 2\cdot \left(\frac{147}{16\sqrt{5}}\right)\cdot \frac{189}{16\sqrt{5}}\cdot \frac{10}{21}} =\sqrt{\left(\frac{168}{8\sqrt{5}}\right)^2 - \left(\frac{7 \cdot 189 \cdot 5}{8 \sqrt{5} \cdot 8\sqrt{5}}\right)}\] Then factoring yields \[\sqrt{\frac{21^2(8^2-15)}{(8\sqrt{5})^2}} =\frac{147}{8\sqrt{5}}\] The area \[[O_{1}AO_{2}] =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot \sin(180^{\circ}-x) =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}\] Now $AK$ is twice the length of the altitude of $\bigtriangleup O_{1}AO_{2}$ so we let the altitude be $h$ and we have \[\frac{1}{2} \cdot h \cdot\frac{147\sqrt{5}}{8\sqrt{5}} =\frac{1}{2} \cdot\frac{147}{16\sqrt{5}} \cdot\frac{189}{16\sqrt{5}} \cdot\frac{8\sqrt{5}}{21}\] \[\implies h =\frac{9}{4}\] Thus our desired length is $\frac{9}{2} \implies n+n = \boxed{11}.$

Solution 4 (Video)

Video Link: https://www.youtube.com/watch?v=nJydO5CLuuI

Solution 5 (Olympiad Geometry)

By the definition of $K$, it is the spiral center mapping $BA\to AC$, which means that it is the midpoint of the $A$-symmedian chord. In particular, if $M$ is the midpoint of $BC$ and $M'$ is the reflection of $A$ across $K$, we have $\triangle ABM'\sim\triangle AMC$. By Stewart's Theorem, it then follows that \[AK = \frac{AM'}{2} = \frac{AC\cdot AB}{2AM} = \frac{7\cdot 9}{2\sqrt{\frac{9^2\cdot 4 + 7^2\cdot 4 - 4^2\cdot 8}{8}}} = \frac{7\cdot 9}{2\sqrt{49}} = \frac{9}{2}\implies m + n = \boxed{11}.\]

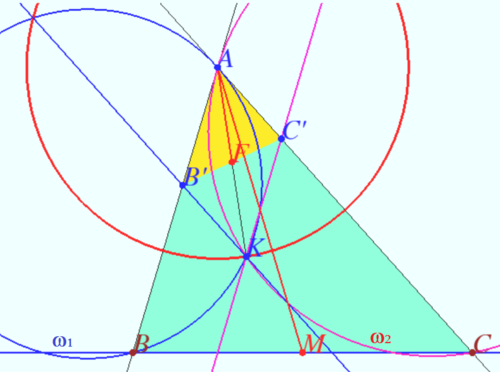
Solution 6 (Inversion simplified)

2019 AIME II 11.png

The median of $\triangle ABC$ is $AM = \sqrt{\frac {AB^2 + AC^2 }{2} – \frac{BC^2}{4}} = 7.$

Consider an inversion with center $A$ and radius $AK$ (inversion with respect the red circle). Let $K, B',$ and $C'$ be inverse points for $K, B,$ and $C,$ respectively.

Image of line $AB$ is line $AB, B'$ lies on this line.

Image of $\omega_2$ is line $KC'||AB$ (circle $\omega_2$ passes through K, C and is tangent to the line $AB$ at point $A.$ Diagram shows circle and its image using same color).

Similarly, $AC||B'K (B'K$ is the image of the circle $\omega_1$).

Therefore $AB'KC'$ is a parallelogram, $AF$ is median of $\triangle AB'C'$ and $AK = 2 AF.$ Then, we have $AB'=\frac{AK^2}{7}$. $\triangle ABC \sim \triangle AC'B'$ with coefficient $k =\frac {AB'}{AC} = \frac{AK^2}{7\cdot 9}.$

So median \[AF = k AM \implies \frac {AK}{2} = AM \cdot k = 7\cdot \frac{AK^2}{7\cdot 9} \implies AK = \frac{9}{2}.\] vladimir.shelomovskii@gmail.com, vvsss

Solution 7 (Heavy Bash)

We start by assigning coordinates to point $A$, labeling it $(0,0)$ and point $B$ at $(7,0)$, and letting point $C$ be above the $x$-axis. Through an application of the Pythagorean Theorem and dropping an altitude to side $AB$, it is easy to see that $C$ has coordinates $(33/7, 24\sqrt{5}/7)$.

Let $O1$ be the center of circle $\omega_1$ and $O2$ be the center of circle $\omega_2$. Since circle $\omega_1$ contains both points $A$ and $B$, $O1$ must lie on the perpendicular bisector of line $AB$, and similarly $O2$ must lie on the perpendicular bisector of line $AC$. Through some calculations, we find that the perpendicular bisector of $AB$ has equation $x = 3.5$, and the perpendicular bisector of $AC$ has equation $y = {-11\sqrt{5}/40 \cdot x} + 189\sqrt{5}/80$.

Since circle $\omega_1$ is tangent to line $AC$ at $A$, its radius must be perpendicular to $AC$ at $A$. Therefore, the radius has equation $y = {{-11\cdot\sqrt{5}/40} \cdot x}$. Substituting the $x$-coordinate of $O1$ into this, we find the y-coordinate of $O1 = {{-11 \cdot \sqrt{5}/40} \cdot 7/2} = {-77 \cdot \sqrt{5}/80}$.

Similarly, since circle $\omega_2$ is tangent to line $AB$ at $A$, its radius must be perpendicular to $AB$ at $A$. Therefore, the radius has equation $x = 0$ and combining with the previous result for $O2$ we get that the coordinates of $O2$ are $(0, 189\sqrt{5}/80)$.

We now find the slope of $O1O2$, the line joining the centers of circles $\omega_1$ and $\omega_2$, which turns out to be ${({266 \cdot \sqrt{5} / 80}) \cdot -2/7} = {-19 \cdot \sqrt{5}/20}$. Since the $y$-intercept of that line is at $O2(0,189\sqrt{5}/80)$, the equation is $y = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}$. Since circles $\omega_1$ and $\omega_2$ intersect at points $A$ and $K$, line $AK$ is the radical axis of those circles, and since the radical axis is always perpendicular to the line joining the centers of the circles, $AK$ has slope ${4 \cdot \sqrt{5}/19}$. Since point $A$ is $(0,0)$, this line has a $y$-intercept of $0$, so it has equation $y$ = ${{4 \cdot \sqrt{5}/19} \cdot x}$.

We set ${{4 \cdot \sqrt{5}/19} \cdot x} = {{-19 \cdot \sqrt{5}/20} \cdot x} + {189 \cdot \sqrt{5}/80}$ in order to find the intersection $I$ of the radical axis $AK$ and $O1O2$. Through some moderate bashing, we find that the intersection point is $I(57/28, {3 \cdot \sqrt{5}/7})$. We know that either intersection point of two circles is the same distance from the intersection of radical axis and line joining the centers of those circles, so reflecting $A$ over $I$ yields $K$ and $AK$ = $2AI$ = (This is the most tedious part of the bash) ${2 \cdot \sqrt{(57/28)^2 + ({3 \cdot \sqrt{5}/7)^2)}}} = {2 \cdot \sqrt{3969/784}} = {2 \cdot 63/28} = {2 \cdot 9/4} = 9/2$. Therefore the answer is $9 + 2 = \boxed{011}.$

See Also

2019 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2019_AIME_II_Problems/Problem_11&oldid=177929"