Difference between revisions of "2015 AIME I Problems/Problem 4"
(→See Also) |
(→Solution 3) |
||
| Line 60: | Line 60: | ||
==Solution 3== | ==Solution 3== | ||
| − | <math> AB = BD, BE = BC, \angle ABE = \angle CBD \implies \triangle ABE= \triangle DBC | + | |
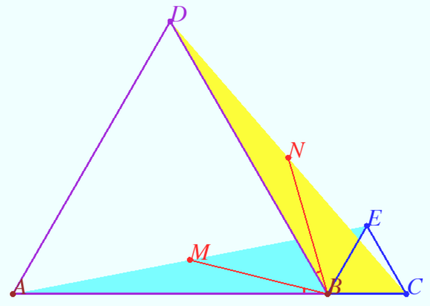
| − | + | [[File:2015 AIME I 4.png|430px|right]] | |
| − | The height of BCE is <math>2 \sqrt{3} \implies \frac {AE^2}{4} =\frac{ (16 + 2)^2 +2^2 \cdot 3}{4} | + | |
| − | <math>BM</math> is the median of <math>\triangle ABE \implies MB^2 = \frac {AB^2}{2} + \frac {BE^2}{2} - \frac {AE^2}{4}=16 \cdot 8 + 4 \cdot 2 – 84 = 52.</math> | + | <math> AB = BD, BE = BC, \angle ABE = \angle CBD \implies \triangle ABE= \triangle DBC</math> |
| − | The area of <math>\triangle BMN</math> | + | |
| + | Medians are equal, so <math>MB = MN, \angle ABM = \angle DBN \implies</math> | ||
| + | <math>\angle MBN = \angle ABD - \angle ABM + \angle DBN = 60^\circ \implies </math> | ||
| + | |||
| + | <math>\triangle MNB</math> is equilateral triangle. | ||
| + | |||
| + | The height of <math>\triangle BCE</math> is <math>2 \sqrt{3},</math> distance from <math>A</math> to midpoint <math>BC</math> is <math>16 + 2 = 18 \implies \frac {AE^2}{4} =\frac{ (16 + 2)^2 +2^2 \cdot 3}{4} = 81 + 3 = 84.</math> | ||
| + | |||
| + | <math>BM</math> is the median of <math>\triangle ABE \implies</math> | ||
| + | <math>MB^2 = \frac {AB^2}{2} + \frac {BE^2}{2} - \frac {AE^2}{4}=16 \cdot 8 + 4 \cdot 2 – 84 = 52.</math> | ||
| + | |||
| + | The area of <math>\triangle BMN</math> | ||
| + | |||
| + | <cmath>[BMN] = \frac{\sqrt{3}}{4} BM^2 =13 \sqrt{3} \implies \boxed{\textbf{507}}.</cmath> | ||
| + | |||
| + | '''vladimir.shelomovskii@gmail.com, vvsss''' | ||
==See Also== | ==See Also== | ||
Revision as of 08:40, 1 September 2022
Problem
Point ![]() lies on line segment
lies on line segment ![]() with
with ![]() and
and ![]() . Points
. Points ![]() and
and ![]() lie on the same side of line
lie on the same side of line ![]() forming equilateral triangles
forming equilateral triangles ![]() and
and ![]() . Let
. Let ![]() be the midpoint of
be the midpoint of ![]() , and
, and ![]() be the midpoint of
be the midpoint of ![]() . The area of
. The area of ![]() is
is ![]() . Find
. Find ![]() .
.
Diagram
![[asy] pair A = (0, 0), B = (16, 0), C = (20, 0), D = (8, 8*sqrt(3)), EE = (18, 2*sqrt(3)), M = (9, sqrt(3)), NN = (14, 4*sqrt(3)); draw(A--B--D--cycle); draw(B--C--EE--cycle); draw(A--EE); draw(C--D); draw(B--M--NN--cycle); dot(A); dot(B); dot(C); dot(D); dot(EE); dot(M); dot(NN); label("A", A, SW); label("B", B, S); label("C", C, SE); label("D", D, N); label("E", EE, N); label("M", M, NW); label("N", NN, NE); [/asy]](http://latex.artofproblemsolving.com/2/2/2/222ea4031f51c1923ced2de0bdf1e1f8e161a1cc.png)
Diagram by RedFireTruck (talk) 18:52, 15 February 2021 (EST)
Solution 1 (fastest)
Let point ![]() be at
be at ![]() . Then,
. Then, ![]() is at
is at ![]() , and
, and ![]() is at
is at ![]() . Due to symmetry, it is allowed to assume
. Due to symmetry, it is allowed to assume ![]() and
and ![]() are in quadrant 1. By equilateral triangle calculations, Point
are in quadrant 1. By equilateral triangle calculations, Point ![]() is at
is at ![]() , and Point
, and Point ![]() is at
is at ![]() . By Midpoint Formula,
. By Midpoint Formula, ![]() is at
is at ![]() , and
, and ![]() is at
is at ![]() . The distance formula shows that
. The distance formula shows that ![]() . Therefore, by equilateral triangle area formula
. Therefore, by equilateral triangle area formula ![]() by Shoelace Theorem,
by Shoelace Theorem, ![]() , so
, so ![]() is
is ![]() .
.
Solution 2
Note that ![]() and
and ![]() . Also,
. Also, ![]() . Thus,
. Thus, ![]() by SAS.
by SAS.
From this, it is clear that a ![]() rotation about
rotation about ![]() will map
will map ![]() to
to ![]() .
This rotation also maps
.
This rotation also maps ![]() to
to ![]() . Thus,
. Thus, ![]() and
and ![]() . Thus,
. Thus, ![]() is equilateral.
is equilateral.
Using the Law of Cosines on ![]() ,
,
![]()
![]() Thus,
Thus, ![]() .
.
Using Stewart's Theorem on ![]() ,
,
![]()
![]()
Calculating the area of ![]() ,
,
![]()
![]() Thus,
Thus, ![]() , so
, so ![]() . Our final answer is
. Our final answer is ![]() .
.
Admittedly, this is much more tedious than the coordinate solutions.
I also noticed that there are two more ways of showing that ![]() is equilateral:
is equilateral:
One way is to show that ![]() ,
, ![]() , and
, and ![]() are related by a spiral similarity centered at
are related by a spiral similarity centered at ![]() .
.
The other way is to use the Mean Geometry Theorem. Note that ![]() and
and ![]() are similar and have the same orientation. Note that
are similar and have the same orientation. Note that ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() ,
, ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() , and
, and ![]() is the weighted average of
is the weighted average of ![]() and
and ![]() . The weights are the same for all three averages. (The weights are actually just
. The weights are the same for all three averages. (The weights are actually just ![]() and
and ![]() , so these are also unweighted averages.) Thus, by the Mean Geometry Theorem,
, so these are also unweighted averages.) Thus, by the Mean Geometry Theorem, ![]() is similar to both
is similar to both ![]() and
and ![]() , which means that
, which means that ![]() is equilateral.
is equilateral.
Solution 3
![]()
Medians are equal, so ![]()
![]()
![]() is equilateral triangle.
is equilateral triangle.
The height of ![]() is
is ![]() distance from
distance from ![]() to midpoint
to midpoint ![]() is
is ![]()
![]() is the median of
is the median of ![]()
![]()
The area of ![]()
![]()
vladimir.shelomovskii@gmail.com, vvsss
See Also
| 2015 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 3 |
Followed by Problem 5 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. ![]()