Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 IMO Problems/Problem 4"

(→‎Solution 3 (Visual))
(→‎Solution 3 (Visual))
Line 39: Line 39:
  
 
==Solution 3 (Visual)==
 
==Solution 3 (Visual)==
 +
[[File:2021 IMO 4b.png|450px|right]]
 
[[File:2021 IMO 4.png|450px|right]]
 
[[File:2021 IMO 4.png|450px|right]]
 
[[File:2021 IMO 4a.png|450px|right]]
 
[[File:2021 IMO 4a.png|450px|right]]
−
[[File:2021 IMO 4b.png|450px|right]]
+
We use the equality of the tangent segments and symmetry.
−
<i><b>Lemma 1</b></i>
+
 +
Using <i><b>Claim 1</b></i> we get <math>\overset{\Large\frown} {TX}</math> symmetric to <math>\overset{\Large\frown} {ZY}</math> with respect <math>IO.</math>
 +
 
 +
Therefore <math>\hspace{10mm} TX = ZY.</math>
 +
 
 +
Let <math>P, Q, N</math> and <math>M</math> be the tangency points of <math>\Gamma</math> with <math>AB, BC, CD</math> and <math>DA</math> respectively.
 +
 
 +
Using Lemma 2 we get <math>TM = QZ, PX = NY.</math>
 +
 
 +
<cmath>AD + DT + XA = AN+ND + TM – MD +XP-PA =</cmath>
 +
<cmath>= XP + TM = QZ + NY = MC + ZC + MD + DY =</cmath>
 +
<cmath>=CD + DY +  ZC.</cmath>
 +
<i><b>Claim 1</b></i>
  
 
Let <math>O</math> be the center of <math>\Omega.</math> Then point <math>T(</math> point <math>X)</math> is symmetryc to <math>Z(Y)</math> with respect <math>IO.</math>
 
Let <math>O</math> be the center of <math>\Omega.</math> Then point <math>T(</math> point <math>X)</math> is symmetryc to <math>Z(Y)</math> with respect <math>IO.</math>
Line 66: Line 79:
 
<cmath>\triangle AIC = \triangle A'IB \implies A'B = AC.</cmath>
 
<cmath>\triangle AIC = \triangle A'IB \implies A'B = AC.</cmath>
  
−
<i><b>Solution</b></i>
+
'''vladimir.shelomovskii@gmail.com, vvsss'''
−
 
 
−
Using Lemma 1 we get <math>\overset{\Large\frown} {TX}</math> symmetric to <math>\overset{\Large\frown} {ZY}</math> with respect <math>IO.</math>
 
−
 
 
−
Therefore <math>\hspace{10mm} TX = ZY.</math>
 
−
 
 
−
Let <math>P, Q, N</math> and <math>M</math> be the tangency points of <math>\Gamma</math> with <math>AB, BC, CD</math> and <math>DA</math> respectively.
 
−
 
 
−
Using Lemma 2 we get <math>TM = QZ, PX = NY.</math>
 
−
 
 
−
<cmath>AD + DT + XA = AN+ND + TM – MD +XP-PA =</cmath>
 
−
<cmath>= XP + TM = QZ + NY = MC + ZC + MD + DY =</cmath>
 
−
<cmath>=CD + DY +  ZC.</cmath>
 
−
'''Shelomovskii, vvsss,  www.deoma-cmd.ru'''
 

Revision as of 21:43, 29 August 2022

Problem

Let $\Gamma$ be a circle with centre $I$, and $ABCD$ a convex quadrilateral such that each of the segments $AB, BC, CD$ and $DA$ is tangent to $\Gamma$. Let $\Omega$ be the circumcircle of the triangle $AIC$. The extension of $BA$ beyond $A$ meets $\Omega$ at $X$, and the extension of $BC$ beyond $C$ meets $\Omega$ at $Z$. The extensions of $AD$ and $CD$ beyond $D$ meet $\Omega$ at $Y$ and $T$, respectively. Prove that \[AD + DT + T X + XA = CD + DY + Y Z + ZC\]

Video Solutions

https://youtu.be/vUftJHRaNx8 [Video contains solutions to all day 2 problems]

https://www.youtube.com/watch?v=U95v_xD5fJk

https://youtu.be/WkdlmduOnRE

Solution

Let $O$ be the centre of $\Omega$.

For $AB=BC$ the result follows simply. By Pitot's Theorem we have \[AB + CD = BC + AD\] so that, $AD = CD.$ The configuration becomes symmetric about $OI$ and the result follows immediately.

Now assume WLOG $AB < BC$. Then $T$ lies between $A$ and $X$ in the minor arc $AX$ and $Z$ lies between $Y$ and $C$ in the minor arc $YC$. Consider the cyclic quadrilateral $ACZX$. We have $\angle CZX = \angle CAB$ and $\angle IAC = \angle IZC$. So that, \[\angle CZX - \angle IZC = \angle CAB - \angle IAC\] \[\angle IZX = \angle IAB\] Since $I$ is the incenter of quadrilateral $ABCD$, $AI$ is the angular bisector of $\angle DBA$. This gives us, \[\angle IZX = \angle IAB = \angle IAD = \angle IAY\] Hence the chords $IX$ and $IY$ are equal. So $Y$ is the reflection of $X$ about $OI$. Hence, \[TX = YZ\] and now it suffices to prove \[AD + DT + XA = CD + DY + ZC\] Let $P, Q, N$ and $M$ be the tangency points of $\Gamma$ with $AB, BC, CD$ and $DA$ respectively. Then by tangents we have, $AD = AM + MD = AP + ND$. So $AD + DT + XA = AP + ND + DT + XA = XP + NT$. Similarly we get, $CD + DY + ZC = ZQ + YM$. So it suffices to prove, \[XP + NT = ZQ + YM\] Consider the tangent $XJ$ to $\Gamma$ with $J \ne P$. Since $X$ and $Y$ are reflections about $OI$ and $\Gamma$ is a circle centred at $I$ the tangents $XJ$ and $YM$ are reflections of each other. Hence \[XP = XJ = YM\] By a similar argument on the reflection of $T$ and $Z$ we get $NT = ZQ$ and finally, \[XP + NT = ZQ + YM\] as required. $QED$

~BUMSTAKA

Solution2

Denote $AD$ tangents to the circle $I$ at $M$, $CD$ tangents to the same circle at $N$; $XB$ tangents at $F$ and $ZB$ tangents at $J$. We can get that $AD=AM+MD;CD=DN+CN$.Since $AM=AF,XA=XF-AM;ZC=ZJ-CN$ Same reason, we can get that $DT=TN-DM;DY=YM-DM$ We can find that $AD+XA+DT=XF+TN;CD+DY+ZC=ZJ+YM$. Connect $IM,IT,IT,IZ,IX,IN,IJ,IF$ separately, we can create two pairs of congruent triangles. In $\triangle{XIF},\triangle{YIM}$, since $\widehat{AI}=\widehat{AI},\angle{FXI}=\angle{MYI}$ After getting that $\angle{IFX}=\angle{IMY};\angle{FXI}=\angle{MYI};IF=IM$, we can find that $\triangle{IFX}\cong \triangle{IMY}$. Getting that $YM=XF$, same reason, we can get that $ZJ=TN$. Now the only thing left is that we have to prove $TX=YZ$. Since $\widehat{IX}=\widehat{IY};\widehat{IT}=\widehat{IZ}$ we can subtract and get that $\widehat{XT}=\widehat{YZ}$,means $XT=YZ$ and we are done ~bluesoul

Solution 3 (Visual)

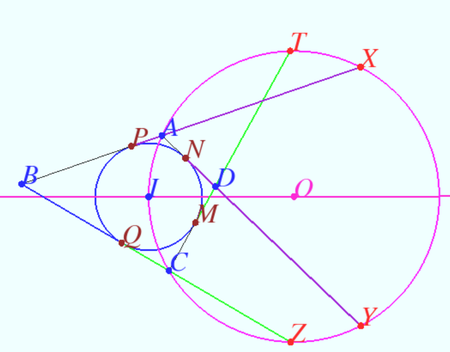
2021 IMO 4b.png
2021 IMO 4.png
2021 IMO 4a.png

We use the equality of the tangent segments and symmetry.

Using Claim 1 we get $\overset{\Large\frown} {TX}$ symmetric to $\overset{\Large\frown} {ZY}$ with respect $IO.$

Therefore $\hspace{10mm} TX = ZY.$

Let $P, Q, N$ and $M$ be the tangency points of $\Gamma$ with $AB, BC, CD$ and $DA$ respectively.

Using Lemma 2 we get $TM = QZ, PX = NY.$

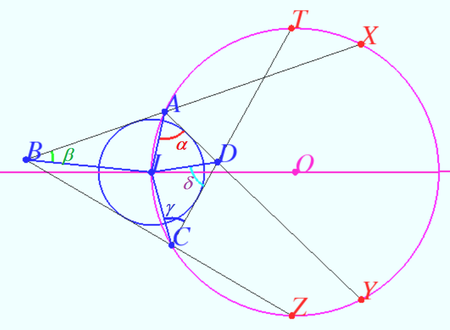
\[AD + DT + XA = AN+ND + TM – MD +XP-PA =\] \[= XP + TM = QZ + NY = MC + ZC + MD + DY =\] \[=CD + DY + ZC.\] Claim 1

Let $O$ be the center of $\Omega.$ Then point $T($ point $X)$ is symmetryc to $Z(Y)$ with respect $IO.$

Proof

Let $\angle BAD =2\alpha, \angle ABC =2\beta, \angle BCD =2\gamma, \angle ADC =2\delta.$

We find measure of some arcs: \[\overset{\Large\frown} {IT}= 2\angle ICT = 2\gamma,\] \[\overset{\Large\frown} {IY}= 2\angle IAY = 2\alpha,\] \[\overset{\Large\frown} {XY}= 2\angle XAY = 2\pi - 4\alpha,\] $\overset{\Large\frown} {IX}= 2\pi - \overset{\Large\frown} {IY} - \overset{\Large\frown} {XY} = 2\alpha =\overset{\Large\frown} {IY}\implies$ symmetry $X$ and $Y.$ \[\overset{\Large\frown} {TZ}= 2\angle DCZ = 2\pi – 4\gamma,\] $\overset{\Large\frown} {IZ}= 2\pi - \overset{\Large\frown} {IT} - \overset{\Large\frown} {TZ}= 2\gamma= \overset{\Large\frown} {IT}\implies$ symmetry $T$ and $Z.$

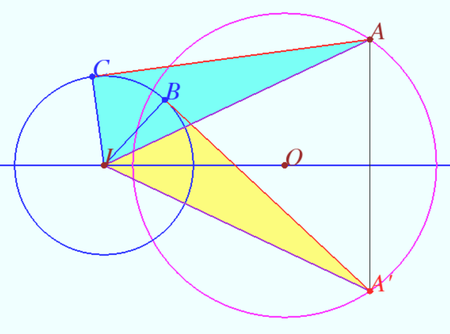
Lemma 2

Let circles $\omega$ centered at $I$ and $\Omega$ centered at $O$ be given. Let points $A$ and $A'$ lies on $\Omega$ and symmetrical with respect $OI.$ Let $AC$ and $A'B$ be tangents to $\omega$. Then $AC = A'B.$

Proof \[AI = A'I, IB = IC, \angle ACI = \angle A'BI = 90^\circ \implies\] \[\triangle AIC = \triangle A'IB \implies A'B = AC.\]

vladimir.shelomovskii@gmail.com, vvsss

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_IMO_Problems/Problem_4&oldid=177681"