Difference between revisions of "2017 AIME II Problems/Problem 15"
(→Solution 3) |
(→Solution 3) |
||
| Line 30: | Line 30: | ||
==Solution 3== | ==Solution 3== | ||
[[File:2017 AIME II 15b.png|300px|right]] | [[File:2017 AIME II 15b.png|300px|right]] | ||
| − | Isosceles tetrahedron or Disphenoid (https://en.wikipedia.org/wiki/Disphenoid) can be inscribed in a circumscribed parallelepiped, whose facial diagonals are the pares of equal edges of the tetrahedron. This parallelepiped is right-angled. The center of the circumscribed sphere coincide with the centroid of the disphenoid. Minimum <math>f(X)</math> occurs at this point, and <math>F(O)= 4R</math>, where <math>R</math> is the circumradius | + | Isosceles tetrahedron <math>ABCD</math> or Disphenoid (https://en.wikipedia.org/wiki/Disphenoid) can be inscribed in a circumscribed parallelepiped <math>AB'CD'C'DA'B,</math> whose facial diagonals are the pares of equal edges of the tetrahedron <math>(AC = B'D'</math> where <math>B'D' = BD).</math> This parallelepiped is right-angled. The center of the circumscribed sphere coincide with the centroid of the disphenoid. Minimum <math>f(X)</math> occurs at this point, and <math>F(O)= 4R</math>, where <math>R</math> is the circumradius |
<cmath>R = OC =\sqrt{\frac {AB^2 + AC^2 + AD^2}{8}}, F(O)= 4R = 4\sqrt {678}.</cmath> | <cmath>R = OC =\sqrt{\frac {AB^2 + AC^2 + AD^2}{8}}, F(O)= 4R = 4\sqrt {678}.</cmath> | ||
Revision as of 03:30, 16 June 2022
Problem
Tetrahedron ![]() has
has ![]() ,
, ![]() , and
, and ![]() . For any point
. For any point ![]() in space, suppose
in space, suppose ![]() . The least possible value of
. The least possible value of ![]() can be expressed as
can be expressed as ![]() , where
, where ![]() and
and ![]() are positive integers, and
are positive integers, and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]() .
.
Official Solution (MAA)
Let ![]() and
and ![]() be midpoints of
be midpoints of ![]() and
and ![]() . The given conditions imply that
. The given conditions imply that ![]() and
and ![]() , and therefore
, and therefore ![]() and
and ![]() . It follows that
. It follows that ![]() and
and ![]() both lie on the common perpendicular bisector of
both lie on the common perpendicular bisector of ![]() and
and ![]() , and thus line
, and thus line ![]() is that common perpendicular bisector. Points
is that common perpendicular bisector. Points ![]() and
and ![]() are symmetric to
are symmetric to ![]() and
and ![]() with respect to line
with respect to line ![]() . If
. If ![]() is a point in space and
is a point in space and ![]() is the point symmetric to
is the point symmetric to ![]() with respect to line
with respect to line ![]() , then
, then ![]() and
and ![]() , so
, so ![]() .
.
Let ![]() be the intersection of
be the intersection of ![]() and
and ![]() . Then
. Then ![]() , from which it follows that
, from which it follows that ![]() . It remains to minimize
. It remains to minimize ![]() as
as ![]() moves along
moves along ![]() .
.
Allow ![]() to rotate about
to rotate about ![]() to point
to point ![]() in the plane
in the plane ![]() on the side of
on the side of ![]() opposite
opposite ![]() . Because
. Because ![]() is a right angle,
is a right angle, ![]() . It then follows that
. It then follows that ![]() , and equality occurs when
, and equality occurs when ![]() is the intersection of
is the intersection of ![]() and
and ![]() . Thus
. Thus ![]() . Because
. Because ![]() is the median of
is the median of ![]() , the Length of Median Formula shows that
, the Length of Median Formula shows that ![]() and
and ![]() . By the Pythagorean Theorem
. By the Pythagorean Theorem ![]() .
.
Because ![]() and
and ![]() are right angles,
are right angles, ![]() It follows that
It follows that ![]() . The requested sum is
. The requested sum is ![]() .
.
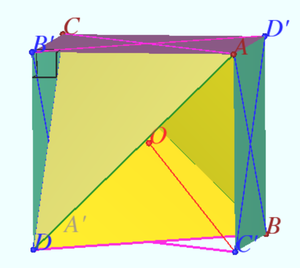
Solution 2
Set ![]() ,
, ![]() ,
, ![]() . Let
. Let ![]() be the point which minimizes
be the point which minimizes ![]() .
.
![]()
![]() Let
Let ![]() and
and ![]() denote the midpoints of
denote the midpoints of ![]() and
and ![]() . From
. From ![]() and
and ![]() , we have
, we have ![]() ,
, ![]() an hence
an hence ![]() is a perpendicular bisector of both segments
is a perpendicular bisector of both segments ![]() and
and ![]() . Then if
. Then if ![]() is any point inside tetrahedron
is any point inside tetrahedron ![]() , its orthogonal projection onto line
, its orthogonal projection onto line ![]() will have smaller
will have smaller ![]() -value; hence we conclude that
-value; hence we conclude that ![]() must lie on
must lie on ![]() . Similarly,
. Similarly, ![]() must lie on the line joining the midpoints of
must lie on the line joining the midpoints of ![]() and
and ![]() .
. ![]()
![]()
![]() Let
Let ![]() be the centroid of triangle
be the centroid of triangle ![]() ; then
; then ![]() (by vectors). If we define
(by vectors). If we define ![]() ,
, ![]() ,
, ![]() similarly, we get
similarly, we get ![]() and so on. But from symmetry we have
and so on. But from symmetry we have ![]() , hence
, hence ![]() .
. ![]()
Now we use the fact that an isosceles tetrahedron has circumradius ![]() .
.
Here ![]() so
so ![]() . Therefore, the answer is
. Therefore, the answer is ![]() .
.
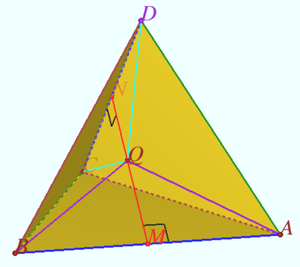
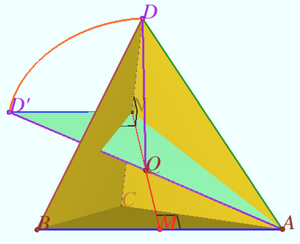
Solution 3
Isosceles tetrahedron ![]() or Disphenoid (https://en.wikipedia.org/wiki/Disphenoid) can be inscribed in a circumscribed parallelepiped
or Disphenoid (https://en.wikipedia.org/wiki/Disphenoid) can be inscribed in a circumscribed parallelepiped ![]() whose facial diagonals are the pares of equal edges of the tetrahedron
whose facial diagonals are the pares of equal edges of the tetrahedron ![]() where
where ![]() This parallelepiped is right-angled. The center of the circumscribed sphere coincide with the centroid of the disphenoid. Minimum
This parallelepiped is right-angled. The center of the circumscribed sphere coincide with the centroid of the disphenoid. Minimum ![]() occurs at this point, and
occurs at this point, and ![]() , where
, where ![]() is the circumradius
is the circumradius
![]()
~vvsss, www.deoma-cmd.ru (Reconstruction)
See Also
| 2017 AIME II (Problems • Answer Key • Resources) | ||
| Preceded by Problem 14 |
Followed by Last Question | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions.