Difference between revisions of "2005 AMC 10A Problems/Problem 17"
(→Solution) |
(→Solution 2) |
||
| Line 13: | Line 13: | ||
==Solution 2== | ==Solution 2== | ||
We know that the smallest number in this sequence must be <math>3 + 5 = 8</math>, and the biggest number must be <math>7 + 9 = 16</math>. Since there are <math>5</math> terms in this sequence, we know that <math>8 + 4d = 16</math>, or that <math>d = 2</math>. Thus, we know that the middle term must be <math>8 + 2 \cdot 2 = \boxed{12}.</math> | We know that the smallest number in this sequence must be <math>3 + 5 = 8</math>, and the biggest number must be <math>7 + 9 = 16</math>. Since there are <math>5</math> terms in this sequence, we know that <math>8 + 4d = 16</math>, or that <math>d = 2</math>. Thus, we know that the middle term must be <math>8 + 2 \cdot 2 = \boxed{12}.</math> | ||
| − | ~yk2007 | + | ~yk2007 (Daniel K.) |
== Video Solution == | == Video Solution == | ||
Revision as of 21:58, 9 May 2022
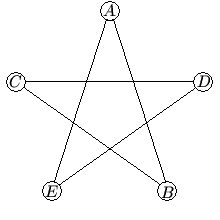
Problem
In the five-sided star shown, the letters 
and 
are replaced by the numbers 
and 
, although not necessarily in this order. The sums of the numbers at the ends of the line segments 
, 
, 
, 
, and 
form an arithmetic sequence, although not necessarily in that order. What is the middle term of the arithmetic sequence?
Solution 1
Each corner 
goes to two sides/numbers. (
goes to 
and , 
goes to 
and ). The sum of every term is equal to 
Since the middle term in an arithmetic sequence is the average of all the terms in the sequence, the middle number is 
Solution 2
We know that the smallest number in this sequence must be 
, and the biggest number must be 
. Since there are 
terms in this sequence, we know that 
, or that 
. Thus, we know that the middle term must be 
~yk2007 (Daniel K.)
Video Solution
https://youtu.be/tKsYSBdeVuw?t=544
~ pi_is_3.14
See Also
| 2005 AMC 10A (Problems • Answer Key • Resources) | ||
| Preceded by Problem 16 |
Followed by Problem 18 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | ||
| All AMC 10 Problems and Solutions | ||
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
