Difference between revisions of "2006 AIME I Problems/Problem 6"
m (→Solution: downsize img) |
(→Solution: alt) |
||
| Line 7: | Line 7: | ||
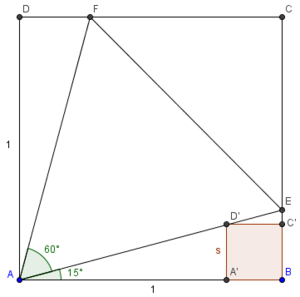
<math>\angle EAF</math> is <math>60</math> degrees, so <math>\angle BAE = \frac{90 - 60}{2} = 15</math>. Thus, <math>\cos 15 = \cos (45 - 30) = \frac{\sqrt{6} + \sqrt{2}}{4} = \frac{1}{AE}</math>, so <math>AE = \frac{4}{\sqrt{6} + \sqrt{2}} \cdot \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}} = \sqrt{6} - \sqrt{2}</math>. Since <math>\triangle AEF</math> is [[equilateral]], <math>EF = AE = \sqrt{6} - \sqrt{2}</math>. <math>\triangle CEF</math> is a <math>45-45-90 \triangle</math>, so <math>CE = \frac{AE}{\sqrt{2}} = \sqrt{3} - 1</math>. Substituting back into the equation from the beginning, we get <math>s^2 = (1 - s)(2 - \sqrt{3} - s)</math>, so <math>(3 - \sqrt{3})s = 2 - \sqrt{3}</math>. Therefore, <math>s = \frac{2 - \sqrt{3}}{3 - \sqrt{3}} \cdot \frac{3 + \sqrt{3}}{3 + \sqrt{3}} = \frac{3 - \sqrt{3}}{6}</math>, and <math>a + b + c = 3 + 3 + 6 = 012</math>. | <math>\angle EAF</math> is <math>60</math> degrees, so <math>\angle BAE = \frac{90 - 60}{2} = 15</math>. Thus, <math>\cos 15 = \cos (45 - 30) = \frac{\sqrt{6} + \sqrt{2}}{4} = \frac{1}{AE}</math>, so <math>AE = \frac{4}{\sqrt{6} + \sqrt{2}} \cdot \frac{\sqrt{6} - \sqrt{2}}{\sqrt{6} - \sqrt{2}} = \sqrt{6} - \sqrt{2}</math>. Since <math>\triangle AEF</math> is [[equilateral]], <math>EF = AE = \sqrt{6} - \sqrt{2}</math>. <math>\triangle CEF</math> is a <math>45-45-90 \triangle</math>, so <math>CE = \frac{AE}{\sqrt{2}} = \sqrt{3} - 1</math>. Substituting back into the equation from the beginning, we get <math>s^2 = (1 - s)(2 - \sqrt{3} - s)</math>, so <math>(3 - \sqrt{3})s = 2 - \sqrt{3}</math>. Therefore, <math>s = \frac{2 - \sqrt{3}}{3 - \sqrt{3}} \cdot \frac{3 + \sqrt{3}}{3 + \sqrt{3}} = \frac{3 - \sqrt{3}}{6}</math>, and <math>a + b + c = 3 + 3 + 6 = 012</math>. | ||
| + | |||
| + | ---- | ||
| + | |||
| + | Here's an alternative geometric way to calculate <math>CE</math> (as opposed to [[trigonometry|trigonometric]]): The diagonal <math>\overline{AC}</math> is made of the [[altitude]] of the equilateral triangle and the altitude of the <math>45-45-90 \triangle</math>. The former is <math>\frac{CE\sqrt{3}}{2}</math>, and the latter is <math>\frac{CE}{2}</math>; thus <math>\frac{CE\sqrt{3} + CE}{2} = AC = \sqrt{2} \Longrightarrow CE = \sqrt{6}-\sqrt{2}</math>. The solution continues as above. | ||
== See also == | == See also == | ||
Revision as of 16:34, 25 September 2007
Problem
Square ![]() has sides of length 1. Points
has sides of length 1. Points ![]() and
and ![]() are on
are on ![]() and
and ![]() respectively, so that
respectively, so that ![]() is equilateral. A square with vertex
is equilateral. A square with vertex ![]() has sides that are parallel to those of
has sides that are parallel to those of ![]() and a vertex on
and a vertex on ![]() The length of a side of this smaller square is
The length of a side of this smaller square is ![]() where
where ![]() and
and ![]() are positive integers and
are positive integers and ![]() is not divisible by the square of any prime. Find
is not divisible by the square of any prime. Find ![]()
Solution
Call the vertices of the new square A', B', C', and D', in relation to the vertices of ![]() , and define
, and define ![]() to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles
to be one of the sides of that square. Since the sides are parallel, by corresponding angles and AA~ we know that triangles ![]() and
and ![]() are similar. Thus, the sides are proportional:
are similar. Thus, the sides are proportional: ![]() . Simplifying, we get that
. Simplifying, we get that ![]() .
.
![]() is
is ![]() degrees, so
degrees, so ![]() . Thus,
. Thus, ![]() , so
, so ![]() . Since
. Since ![]() is equilateral,
is equilateral, ![]() .
. ![]() is a
is a ![]() , so
, so ![]() . Substituting back into the equation from the beginning, we get
. Substituting back into the equation from the beginning, we get ![]() , so
, so ![]() . Therefore,
. Therefore, ![]() , and
, and ![]() .
.
Here's an alternative geometric way to calculate ![]() (as opposed to trigonometric): The diagonal
(as opposed to trigonometric): The diagonal ![]() is made of the altitude of the equilateral triangle and the altitude of the
is made of the altitude of the equilateral triangle and the altitude of the ![]() . The former is
. The former is ![]() , and the latter is
, and the latter is ![]() ; thus
; thus ![]() . The solution continues as above.
. The solution continues as above.
See also
| 2006 AIME I (Problems • Answer Key • Resources) | ||
| Preceded by Problem 5 |
Followed by Problem 7 | |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 | ||
| All AIME Problems and Solutions | ||