Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 Fall AMC 10B Problems/Problem 23"

(→‎Solution)
(→‎Solution 2 (Ramsey's Theorem))
Line 23: Line 23:
  
 
This problem is related to a special case of [https://en.wikipedia.org/wiki/Ramsey%27s_theorem Ramsey's Theorem], [https://en.wikipedia.org/wiki/Ramsey%27s_theorem#R(3,_3)_=_6 R(3, 3) = 6]. Suppose we color every edge of a complete <math>6</math> vertex graph <math>(K_6)</math> with <math>2</math> colors, there must exist a <math>3</math> vertex complete graph <math>(K_3)</math> with all it's edges in the same color. That is, <math>K_6</math> contains a monochromatic <math>K_3</math>.
 
This problem is related to a special case of [https://en.wikipedia.org/wiki/Ramsey%27s_theorem Ramsey's Theorem], [https://en.wikipedia.org/wiki/Ramsey%27s_theorem#R(3,_3)_=_6 R(3, 3) = 6]. Suppose we color every edge of a complete <math>6</math> vertex graph <math>(K_6)</math> with <math>2</math> colors, there must exist a <math>3</math> vertex complete graph <math>(K_3)</math> with all it's edges in the same color. That is, <math>K_6</math> contains a monochromatic <math>K_3</math>.
 +
 +
Choose the top vertex of the pentagon, there will be <math>4</math> sides\diagonals radiating outward from it. When all <math>4</math> sides\diagonals are the same color, there must be a same colored triangle.
 +
 +
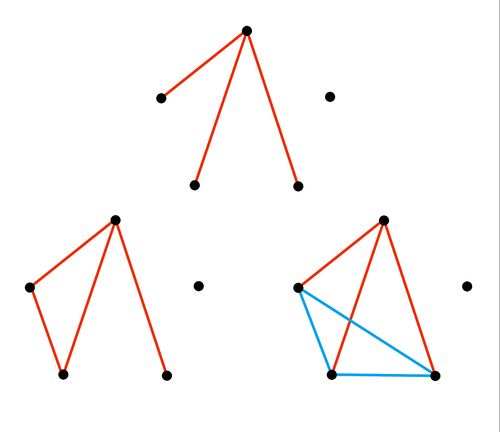
When <math>3</math> sides\diagonals are the same color, suppose red. There must be a same colored triangle as shown in the diagram below.
 +
 +
[[File:K 5 3 colors.jpg | 500px]]
 +
 +
[[File:K 5 2 colors.jpg | 500px]]
  
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]
 
~[https://artofproblemsolving.com/wiki/index.php/User:Isabelchen isabelchen]

Revision as of 02:58, 1 January 2022

Problem

Each of the $5{ }$ sides and the $5{ }$ diagonals of a regular pentagon are randomly and independently colored red or blue with equal probability. What is the probability that there will be a triangle whose vertices are among the vertices of the pentagon such that all of its sides have the same color?

$(\textbf{A})\: \frac23\qquad(\textbf{B}) \: \frac{105}{128}\qquad(\textbf{C}) \: \frac{125}{128}\qquad(\textbf{D}) \: \frac{253}{256}\qquad(\textbf{E}) \: 1$

Solution 1

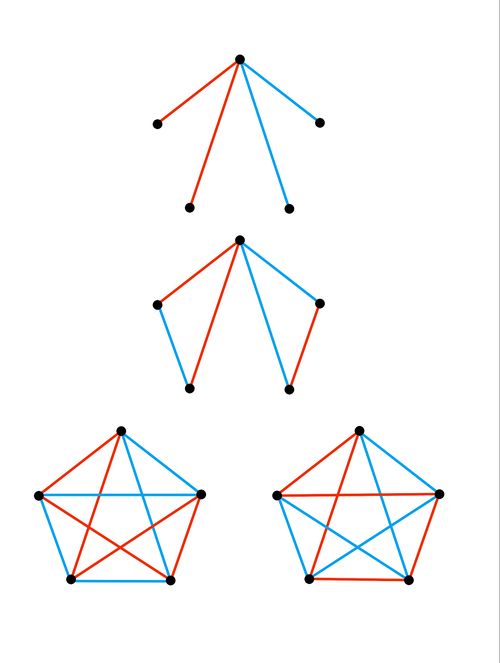
Instead of finding the probability of a same-colored triangle appearing, let us find the probability that one does not appear. After drawing the regular pentagon out, note the topmost vertex; it has 4 sides/diagonals emanating outward from it. We do casework on the color distribution of these sides/diagonals.

$\textbf{Case 1}$: all 4 are colored one color. In that case, all of the remaining sides must be of the other color to not have a triangle where all three sides are of the same color. We can correspondingly fill out each color based on this constraint, but in this case you will always end up with a triangle where all three sides have the same color by inspection.

$\textbf{Case 2}$: 3 are one color and one is the other. Following the steps from the previous case, you can try filling out the colors, but will always arrive at a contradiction so this case does not work either.

$\textbf{Case 3}$: 2 are one color and 2 are of the other color. Using the same logic as previously, we can color the pentagon 2 different ways by inspection to satisfy the requirements. There are ${4\choose2}$ ways to color the original sides/diagonals and 2 ways after that to color the remaining ones for a total of $6\cdot 2 = 12$ ways to color the pentagon so that no such triangle has the same color for all of its sides.

These are all the cases, and there are a total of $2^{10}$ ways to color the pentagon. Therefore the answer is $1-\frac{12}{1024} = 1-\frac{3}{256} = \frac{253}{256} = \boxed{D}$

~KingRavi

Solution 2 (Ramsey's Theorem)

This problem is related to a special case of Ramsey's Theorem, R(3, 3) = 6. Suppose we color every edge of a complete $6$ vertex graph $(K_6)$ with $2$ colors, there must exist a $3$ vertex complete graph $(K_3)$ with all it's edges in the same color. That is, $K_6$ contains a monochromatic $K_3$.

Choose the top vertex of the pentagon, there will be $4$ sides\diagonals radiating outward from it. When all $4$ sides\diagonals are the same color, there must be a same colored triangle.

When $3$ sides\diagonals are the same color, suppose red. There must be a same colored triangle as shown in the diagram below.

K 5 3 colors.jpg

K 5 2 colors.jpg

~isabelchen

See Also

2021 Fall AMC 10B (Problems • Answer Key • Resources)
Preceded by
Problem 22 		Followed by
Problem 24
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_Fall_AMC_10B_Problems/Problem_23&oldid=169035"