Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2018 AMC 10A Problems/Problem 10"

(→‎Solution 6 (Symmetric Substitution))
Line 87: Line 87:
  
 
~BakedPotato66
 
~BakedPotato66
 +
 +
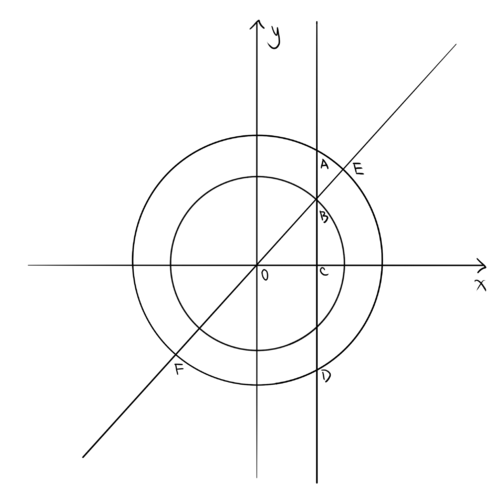
===Solution 8 (Analytic Geometry)===
 +
 +
[[File:2018 AMC10 A P10.PNG|500px]]
 +
 +
~isabelchen
  
 
== Video Solutions ==
 
== Video Solutions ==

Revision as of 00:35, 23 October 2021

Problem

Suppose that real number $x$ satisfies \[\sqrt{49-x^2}-\sqrt{25-x^2}=3\]What is the value of $\sqrt{49-x^2}+\sqrt{25-x^2}$?

$\textbf{(A) }8\qquad \textbf{(B) }\sqrt{33}+8\qquad \textbf{(C) }9\qquad \textbf{(D) }2\sqrt{10}+4\qquad \textbf{(E) }12\qquad$

Solutions

Solution 1

In order to eliminate the square roots, we multiply by the conjugate. Its value is the solution. The $x^2$ terms cancel nicely. $(\sqrt {49-x^2} + \sqrt {25-x^2})(\sqrt {49-x^2} - \sqrt {25-x^2}) = 49-x^2 - 25 +x^2 = 24$

Given that $(\sqrt {49-x^2} - \sqrt {25-x^2}) = 3, (\sqrt {49-x^2} + \sqrt {25-x^2}) = \frac {24} {3} = \boxed{\textbf{(A) } 8}$. - cookiemonster2004

Solution 2

Let $u=\sqrt{49-x^2}$, and let $v=\sqrt{25-x^2}$. Then $v=\sqrt{u^2-24}$. Substituting, we get $u-\sqrt{u^2-24}=3$. Rearranging, we get $u-3=\sqrt{u^2-24}$. Squaring both sides and solving, we get $u=\frac{11}{2}$ and $v=\frac{11}{2}-3=\frac{5}{2}$. Adding, we get that the answer is $\boxed{\textbf{(A) } 8}$.

Solution 3

Put the equations to one side. $\sqrt{49-x^2}-\sqrt{25-x^2}=3$ can be changed into $\sqrt{49-x^2}=\sqrt{25-x^2}+3$.

We can square both sides, getting us $49-x^2=(25-x^2)+(3^2)+ 2\cdot 3 \cdot \sqrt{25-x^2}.$

That simplifies out to $15=6 \sqrt{25-x^2}.$ Dividing both sides by $6$ gets us $\frac{5}{2}=\sqrt{25-x^2}$.

Following that, we can square both sides again, resulting in the equation $\frac{25}{4}=25-x^2$. Simplifying that, we get $x^2 = \frac{75}{4}$.

Substituting into the equation $\sqrt{49-x^2}+\sqrt{25-x^2}$, we get $\sqrt{49-\frac{75}{4}}+\sqrt{25-\frac{75}{4}}$. Immediately, we simplify into $\sqrt{\frac{121}{4}}+\sqrt{\frac{25}{4}}$. The two numbers inside the square roots are simplified to be $\frac{11}{2}$ and $\frac{5}{2}$, so you add them up: $\frac{11}{2}+\frac{5}{2}=\boxed{\textbf{(A) 8}}$.

~kevinmathz

Solution 4 (Geometric Interpretation)

Draw a right triangle $ABC$ with a hypotenuse $AC$ of length $7$ and leg $AB$ of length $x$. Draw $D$ on $BC$ such that $AD=5$. Note that $BC=\sqrt{49-x^2}$ and $BD=\sqrt{25-x^2}$. Thus, from the given equation, $BC-BD=DC=3$. Using Law of Cosines on triangle $ADC$, we see that $\angle{ADC}=120^{\circ}$ so $\angle{ADB}=60^{\circ}$. Since $ADB$ is a $30-60-90$ triangle, $\sqrt{25-x^2}=BD=\frac{5}{2}$ and $\sqrt{49-x^2}=\frac{5}{2}+3=\frac{11}{2}$. Finally, $\sqrt{49-x^2}+\sqrt{25-x^2}=\frac{5}{2}+\frac{11}{2}=\boxed{\textbf{(A)~8}}$. [asy] var s = sqrt(3); pair A = (-5*s/2, 0); pair B = (0,0); pair C = (0,5.5); pair D = (0,2.5); draw(A--B--C--A--D); rightanglemark(A, B, D); label("A", A, SW); label("B", B, SE); label("C", C, NE); label("D", D, E); label("7", (-5*s/4, 5.5/2), NW); label("120$^\circ$", D, NW); label("60$^\circ$", (0,2), SW); label("$x$", 0.5*A, S); draw(rightanglemark(A, B, C)); draw(anglemark(A, D, B)); markscalefactor = 0.04; draw(anglemark(C, D, A)); label("$\frac{5}{2}$", (0,1.25), E); label("3", (0,4), E); label("5", (-5*s/4, 5/4), N); [/asy]

Solution 5 (No Square Roots, Fastest)

We notice that the two expressions are conjugates, and therefore we can write them in a "difference-of-squares" format. Namely, we can write it as $((49-x^2) - (25 - x^2)) = (49 - x^2 - 25 + x^2) = 24$. Given the $3$ in the problem, we can divide $24 / 3 = \boxed{\textbf{(A) } 8}$.

-aze.10

Solution 6 (Symmetric Substitution)

Since $\frac{25+49}{2}=37$, let $37-x^2 = y$. Then we have $\sqrt{y+12}-\sqrt{y-12}=3$. Squaring both sides gives us $2y-2\sqrt{y^2-144}=9$. Isolating the term with the square root, and squaring again, we get $4y^2-36y+81=4y^2-576 \implies y=\frac{73}{4}$. Then $\sqrt{y+12}+\sqrt{y-12} = \sqrt{\frac{121}{4}}+\sqrt{\frac{25}{4}} = \frac{16}{2}=\boxed{8}$.

Solution 7 (Difference of Squares)

Let $\sqrt{49-x^2}=a$ and $\sqrt{25-x^2}=b$. Then by difference of squares:

$(a+b)(a-b)=a^2-b^2$.

We can simplify this expression to get our answer. $a^2-b^2=(49-x^2)-(25-x^2)=24$ and from the given statement, $a-b=3$. Now we have:

$(a+b)(3)=24$.

Hence, $a+b=\sqrt{49-x^2}-\sqrt{25-x^2}=8$ so our answer is $\boxed{\textbf{(A) } 8}$.

~BakedPotato66

Solution 8 (Analytic Geometry)

2018 AMC10 A P10.PNG

~isabelchen

Video Solutions

Video Solution 1

https://youtu.be/ba6w1OhXqOQ?t=1403

~ pi_is_3.14

Video Solution 2

https://youtu.be/zQG70XKAdeA ~ North America Math Contest Go Go Go

Video Solution 3

https://youtu.be/ZiZVIMmo260

Video Solution 4

https://youtu.be/5cA87rbzFdw

~savannahsolver

See Also

2018 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 9 		Followed by
Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions
Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2018_AMC_10A_Problems/Problem_10&oldid=163933"