Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2021 USAJMO Problems/Problem 2"

m (→‎Solution)
m (→‎Solution)
Line 7: Line 7:
 
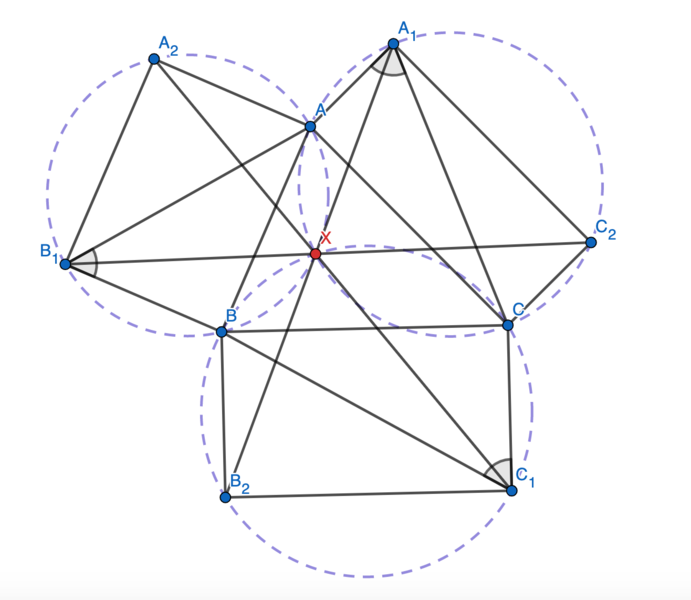
We first claim that the three circles <math>(BCC_1B_2),</math> <math>(CAA_1C_2),</math> and <math>(ABB_1A_2)</math> share a common intersection.
 
We first claim that the three circles <math>(BCC_1B_2),</math> <math>(CAA_1C_2),</math> and <math>(ABB_1A_2)</math> share a common intersection.
  
−
Let the second intersection of <math>(BCC_1B_2)</math> and <math>(CAA_1C_2)</math> be <math>K</math>. Then  
+
Let the second intersection of <math>(BCC_1B_2)</math> and <math>(CAA_1C_2)</math> be <math>X</math>. Then  
 
<cmath>\begin{align*}
 
<cmath>\begin{align*}
−
\angle AKC &= 360^\circ - \angle BKA - \angle CKB \\
+
\angle AXC &= 360^\circ - \angle BXA - \angle CXB \\
 
&= 360^\circ - (180^\circ - \angle AB_1B + 180^\circ - \angle BC_1C) \\&
 
&= 360^\circ - (180^\circ - \angle AB_1B + 180^\circ - \angle BC_1C) \\&
 
= 180^\circ - \angle CA_1A,
 
= 180^\circ - \angle CA_1A,
 
\end{align*}</cmath>
 
\end{align*}</cmath>
−
which implies that <math>AA_1C_2CK</math> is cyclic as desired.
+
which implies that <math>AA_1C_2CX</math> is cyclic as desired.
  
−
Now we show that <math>K</math> is the intersection of <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2.</math> Note that <math>\angle C_1XB = \angle BXA_2 = 90^\circ,</math> so <math>A_2, K, C_1</math> are collinear. Similarly, <math>B_1, K, C_2</math> and <math>A_1, K, B_2</math> are collinear, so the three lines concur and we are done.
+
Now we show that <math>X</math> is the intersection of <math>B_1C_2,</math> <math>C_1A_2,</math> and <math>A_1B_2.</math> Note that <math>\angle C_1XB = \angle BXA_2 = 90^\circ,</math> so <math>A_2, X, C_1</math> are collinear. Similarly, <math>B_1, X, C_2</math> and <math>A_1, X, B_2</math> are collinear, so the three lines concur and we are done.
  
 
~Leonard_my_dude
 
~Leonard_my_dude

Revision as of 20:03, 19 April 2021

Problem

Rectangles $BCC_1B_2,$ $CAA_1C_2,$ and $ABB_1A_2$ are erected outside an acute triangle $ABC.$ Suppose that\[\angle BC_1C+\angle CA_1A+\angle AB_1B=180^{\circ}.\]Prove that lines $B_1C_2,$ $C_1A_2,$ and $A_1B_2$ are concurrent.

Solution

Leonard my dude.png

We first claim that the three circles $(BCC_1B_2),$ $(CAA_1C_2),$ and $(ABB_1A_2)$ share a common intersection.

Let the second intersection of $(BCC_1B_2)$ and $(CAA_1C_2)$ be $X$. Then \begin{align*} \angle AXC &= 360^\circ - \angle BXA - \angle CXB \\ &= 360^\circ - (180^\circ - \angle AB_1B + 180^\circ - \angle BC_1C) \\& = 180^\circ - \angle CA_1A, \end{align*} which implies that $AA_1C_2CX$ is cyclic as desired.

Now we show that $X$ is the intersection of $B_1C_2,$ $C_1A_2,$ and $A_1B_2.$ Note that $\angle C_1XB = \angle BXA_2 = 90^\circ,$ so $A_2, X, C_1$ are collinear. Similarly, $B_1, X, C_2$ and $A_1, X, B_2$ are collinear, so the three lines concur and we are done.

~Leonard_my_dude

See Also

2021 USAJMO (Problems • Resources)
Preceded by
Problem 1 		Followed by
Problem 3
1 • 2 • 3 • 4 • 5 • 6
All USAJMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2021_USAJMO_Problems/Problem_2&oldid=151987"