Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2007 Cyprus MO/Lyceum/Problems"

(→‎Problem 23)
(→‎Problem 25)
Line 351: Line 351:
  
 
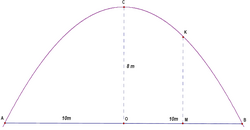
== Problem 25 ==
 
== Problem 25 ==
−
{{image}}
+
<div style="float:right">
 +
[[Image:2007 CyMO-25.PNG|250px]]
 +
</div>
  
 
[[2007 Cyprus MO/Lyceum/Problem 25|Solution]]
 
[[2007 Cyprus MO/Lyceum/Problem 25|Solution]]
−
 
  
 
== Problem 26 ==
 
== Problem 26 ==

Revision as of 08:41, 8 May 2007

Problem 1

If $x-y=1$, then the value of the expression $K=x^2+x-2xy+y^2-y$ is

A. $2$

B. $-2$

C. $1$

D. $-1$

E. $0$

Solution

Problem 2

Given the formula $f(x) = 4^x$, then $f(x+1)-f(x)$ equals to

A. $4$

B. $4^x$

C. $2\cdot4^x$

D. $4^{x+1}$

E. $3\cdot4^x$

Solution

Problem 3

A cyclist drives form town A to town B with velocity $40 \frac{\mathrm{km}}{\mathrm{h}}$ and comes back with velocity $60 \frac{\mathrm{km}}{\mathrm{h}}$. The mean velocity in $\frac{\mathrm{km}}{\mathrm{h}}$ for the total distance is

A. $45$

B. $48$

C. $50$

D. $55$

E. $100$

Solution

Problem 4

We define the operation $a*b = \frac{1+a}{1+b^2}$, $\forall a,b \in \real$.

The value of $(2*0)*1$ is

A. $2$

B. $1$

C. $0$

D. $\frac{1}{2}$

E. $\frac{5}{2}$


Solution

Problem 5

If the remainder of the division of $a$ with $35$ is $23$, then the remainder of the division of $a$ with $7$ is

A. $1$

B. $2$

C. $3$

D. $4$

E. $5$

Solution

Problem 6

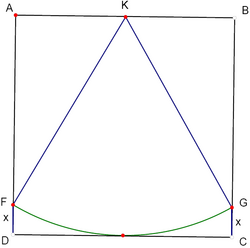
2007 CyMO-6.PNG

$ABCD$ is a square of side length 2 and $FG$ is an arc of the circle with centre the midpoint $K$ of the side $AB$ and radius 2. The length of the segments $FD=GC=x$ is

A. $\frac{1}{4}$

B. $\frac{\sqrt{2}}{2}$

C. $2-\sqrt{3}$

D. $\sqrt{3}-1$

E. $\sqrt{2}$$-1$


Solution

Problem 7

If a diagonal $d$ of a rectangle forms a $60^\circ$ angle with one of its sides, then the area of the rectangle is

A. $\frac{d^2 \sqrt{3}}{4}$

B. $\frac{d^2}{2}$

C. $2d^2$

D. $d^2 \sqrt{2}$

E. None of these

Solution

Problem 8

If we subtract from 2 the inverse number of $x-1$, we get the inverse of $x-1$. Then the number $x+1$ equals to

A. $0$

B. $1$

C. $-1$

D. $3$

E. $\frac{1}{2}$

Solution

Problem 9

We consider the sequence of real numbers $a_1,a_2,a_3,...$ such that $a_1=0$, $a_2=1$ and $a_n=a_{n-1}-a_{n-2}$, $\forall n \in \{3,4,5,6,...\}$. The value of the term $a_{138}$ is

A. $0$

B. $-1$

C. $1$

D. $2$

E. $-2$

Solution

Problem 10

The volume of an orthogonal parallelepiped is $132\;\mathrm{cm}^3$ and its dimensions are integers. The minimum sum of the dimensions is

A. $27\;\mathrm{ cm}$

B. $19\;\mathrm{ cm}$

C. $20\;\mathrm{ cm}$

D. $18\;\mathrm{ cm}$

E. None of these

Solution

Problem 11

If $X=\frac{1}{2007 \sqrt{2006}+2006 \sqrt{2007}}$ and $Y=\frac{1}{\sqrt{2006}}-\frac{1}{\sqrt{2007}}$, which of the following is correct?

A. $X=2Y$

B. $Y=2X$

C. $X=Y$

D. $X=Y^2$

E. $Y=X^2$

Solution

Problem 12

The function $f : \Re \rightarrow \Re$ has the properties $f(0) = -1$ and $f(xy)+f(x)+f(y)=x+y+xy+k$ $\forall x,y \in \Re$, where $k \in \Re$ is a constant. The value of $f(-1)$ is

A. $1$

B. $-1$

C. $0$

D. $-2$

E. $3$

Solution

Problem 13

If $x_1,x_2$ are the roots of the equation $x^2+ax+1=0$ and $x_3,x_4$ are the roots of the equation $x^2+bx+1=0$, then the expression $\frac{x_1}{x_2x_3x_4}+\frac{x_2}{x_1x_3x_4}+ \frac{x_3}{x_1x_2x_4}+\frac{x_4}{x_1x_2x_3}$equals to

A. $a^2+b^2-2$

B. $a^2+b^2$

C. $\frac{a^2+b^2}{2}$

D. $a^2+b^2+1$

E. $a^2+b^2-4$

Solution

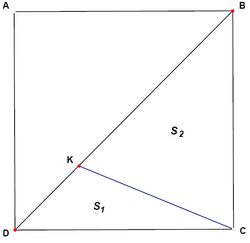
Problem 14

2007 CyMO-14.PNG

In the square $ABCD$ the segment $KB$ equals a side of the square. The ratio of areas $\frac{S_1}{S_2}$ is

A. $\frac{1}{3}$

B. $\frac{2}{3}$

C. $\frac{1}{\sqrt{2}}$

D. $\sqrt2 -1$

E. $\frac{\sqrt{2}}{4}$

Solution

Problem 15

2007 CyMO-15.PNG

The reflex angles of the concave octagon $ABCDEFGH$ measure $240^\circ$ each. Diagonals $AE$ and $GC$ are perpendicular, bisect each other, and are both equal to $2$.

The area of the octagon is

A. $\frac{6-2\sqrt{3}}{3}$

B. $8$

C. $1$

D. $\frac{6+2\sqrt{3}}{3}$

E. None of these

Solution

Problem 16

The full time score of a football match was $3$-$2$. how many possible half time results can we have for this match?

A. $5$

B. $6$

C. $10$

D. $11$

E. $12$

Solution

Problem 17

The last digit of the number $a=2^{2007}+3^{2007}+5^{2007}+7^{2007}$ is

A. $0$

B. $2$

C. $4$

D. $6$

E. $8$

Solution

Problem 18

How many subsets are there for the set $A=\{1,2,3,4,5,6,7\}$?

A. $7$

B. $14$

C. $49$

D. $64$

E. $128$

Solution

Problem 19

120 five-digit numbers can be written with the digits $1,2,3,4,5$. If we place these numbers in increasing order, then the position of the number $41253$ is

A. $71^{st}$

B. $72^{nd}$

C. $73^{rd}$

D. $74^{th}$

E. None of these

Solution

Problem 20

The mean value for 9 Math-tests that a student succeded was $10$ (in scale $0$-$20$). If we put the grades of these tests in incresing order, then the maximum grade of the $5^{th}$ test is

A. $15$

B. $16$

C. $17$

D. $18$

E. $19$

Solution

Problem 21

2007 CyMO-21.PNG

Solution

Problem 22

2007 CyMO-22.PNG

Solution

Problem 23

2007 CyMO-23.PNG

Solution

Problem 24

Costas sold two televisions for €198 each. From the sale of the first one he made a profit of 10% on its value and from the sale of the second one, he had a loss of 10% on its value. After the sale of the two televisions Costas had in total

A. profit €4

B. neither profit nor loss

C. loss €8

D. profit €8

E. loss €4

Solution

Problem 25

2007 CyMO-25.PNG

Solution

Problem 26

The number of boys in a school is 3 times the number of girls and the number of girls is 9 times the number of teachers. Let us denote with $b$, $g$ and $t$, the number of boys, girls and teachers respectively. Then the total number of boys, girls and teachers equals to

A. $31b$

B. $\frac{37b}{27}$

C. $13g$

D. $\frac{37g}{27}$

E. $\frac{37t}{27}$

Solution

Problem 27

An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.

Solution


Problem 28

The product of $15^8\cdot28^6\cdot5^{11}$ is an integer number whose last digits are zeros. How many zeros are there?

A. $6$

B. $8$

C. $11$

D. $12$

E. $19$

Solution

Problem 29

The minimum value of a positive integer $k$, for which the sum $S=k+(k+1)+(k+2)+\ldots+(k+10)$ is a perfect square, is

A. $5$

B. $6$

C. $10$

D. $11$

E. None of these

Solution

Problem 30

An image is supposed to go here. You can help us out by creating one and editing it in. Thanks.

Solution


See also

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2007_Cyprus_MO/Lyceum/Problems&oldid=15031"