Difference between revisions of "User:Vqbc/Testing"

Revision as of 22:27, 26 June 2021

Statement

Given a triangle $\triangle ABC$ with sides of length $a, b, c$ opposite vertices are $A$ , $B$ , $C$ , respectively. If cevian $AD$ is drawn so that $BD = m$ , $DC = n$ and $AD = d$ , we have that $b^2m + c^2n = amn + d^2a$ . (This is also often written $man + dad = bmb + cnc$ , a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")

Proof

Applying the Law of Cosines in triangle $\triangle ABD$ at angle $\angle ADB$ and in triangle $\triangle ACD$ at angle $\angle CDA$ , we get the equations

$n^{2} + d^{2} - 2\ce{nd}\cos{\angle CDA} = b^{2}$
$m^{2} + d^{2} - 2\ce{md}\cos{\angle ADB} = c^{2}$

Because angles $\angle ADB$ and $\angle CDA$ are supplementary, $m\angle ADB = 180^\circ - m\angle CDA$ . We can therefore solve both equations for the cosine term. Using the trigonometric identity $\cos{\theta} = -\cos{(180^\circ - \theta)}$ gives us

$\frac{n^2 + d^2 - b^2}{2nd} = \cos{\angle CDA}$

$\frac{c^2 - m^2 -d^2}{2md} = \cos{\angle CDA}$

Setting the two left-hand sides equal and clearing denominators, we arrive at the equation: $c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n$ . However, $m+n = a$ so $m^2n + n^2m = (m + n)mn = amn$ and $d^2m + d^2n = d^2(m + n) = d^2a.$ This simplifies our equation to yield $c^2n + b^2m = amn + d^2a,$ or Stewart's theorem.

@@ Line 1: / Line 1: @@
-The '''discriminant''' of a [[quadratic equation]] of the form <math>a{x}^2+b{x}+{c}=0</math> is the quantity <math>b^2-4ac</math>.  When <math>{a},{b},{c}</math> are real, this is a notable quantity, because if the discriminant is positive, the equation has two [[real]] [[root]]s; if the discriminant is negative, the equation has two [[nonreal]] roots; and if the discriminant is 0, the equation has a real [[double root]].
+== Statement ==
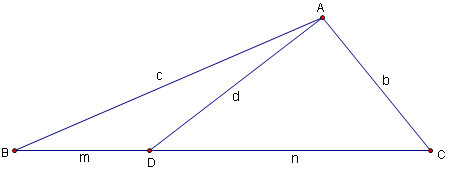
+Given a [[triangle]] <math>\triangle ABC</math> with sides of length <math>a, b, c</math> opposite [[vertex | vertices]] are <math>A</math>, <math>B</math>, <math>C</math>, respectively.  If [[cevian]] <math>AD</math> is drawn so that <math>BD = m</math>, <math>DC = n</math> and <math>AD = d</math>, we have that <math>b^2m + c^2n = amn + d^2a</math>.  (This is also often written <math>man + dad = bmb + cnc</math>, a form which invites mnemonic memorization, i.e. "A man and his dad put a bomb in the sink.")
-==Discriminant of polynomials of degree n==
+<center>[[Image:Stewart's_theorem.png]]</center>
-The discriminant can tell us something about the roots of a given polynomial <math>p(x)=a_nx^n+a_{n-1}x^{n-1}+...+a_0</math> of degree <math>n</math> with all the coefficients being real. But for polynomials of degree 4 or higher it can be difficult to use it.
+== Proof ==
+Applying the [[Law of Cosines]] in triangle <math>\triangle ABD</math> at [[angle]] <math>\angle ADB</math> and in triangle <math>\triangle ACD</math> at angle <math>\angle CDA</math>, we get the equations
+*<math> n^{2} + d^{2} - 2\ce{nd}\cos{\angle CDA} = b^{2} </math>
+*<math> m^{2} + d^{2} - 2\ce{md}\cos{\angle ADB} = c^{2} </math>
-===General formula of discriminant===
+Because angles <math>\angle ADB</math> and <math>\angle CDA</math> are [[supplementary]], <math>m\angle ADB = 180^\circ - m\angle CDA</math>.  We can therefore solve both equations for the cosine term.  Using the [[trigonometric identity]] <math>\cos{\theta} = -\cos{(180^\circ - \theta)}</math> gives us
+*<math> \frac{n^2 + d^2 - b^2}{2nd} = \cos{\angle CDA}</math>
-We know that the discriminant of a polynomial is the product of the squares of the differences of the polynomial roots <math>r_i</math>, so,
+*<math> \frac{c^2 - m^2 -d^2}{2md} = \cos{\angle CDA}</math>
-<math>D(p)=a_n^{2n-2}\prod_{i<j}^{n}(r_i-r_j)^2</math>
+Setting the two left-hand sides equal and clearing [[denominator]]s, we arrive at the equation: <math> c^{2}n + b^{2}m=m^{2}n +n^{2}m + d^{2}m + d^{2}n </math>.
+However,
+<math>m+n = a</math> so
+<cmath>m^2n + n^2m = (m + n)mn = amn</cmath> and
+<cmath>d^2m + d^2n = d^2(m + n) = d^2a.</cmath>
+This simplifies our equation to yield <math>c^2n + b^2m = amn + d^2a,</math> or Stewart's theorem.
-====When <math>n=2</math>====
+== See also ==
+* [[Menelaus' theorem]]
+* [[Ceva's theorem]]
+* [[Geometry]]
+* [[Angle Bisector theorem]]
-Given a polynomial <math>p(x)=ax^2+bx+c</math>, its discriminant is <math>D(p)=b^2-4ac</math>, wich can also be denoted by <math>\Delta=b^2-4ac</math>.
+[[Category:Geometry]]
-For <math>\Delta>0</math> we have the graph
+[[Category:Theorems]]
-[[Image:Delta_greater_than_0.png|thumb|center|300x300px|link=Gmass]]
-wich has two distinct real roots.
-For <math>\Delta<0</math> we have the graph
-[[File:Delta_lower_than_0.png|thumb|center|300x300px]]
-wich has two non-real roots.
-And for the case <math>\Delta=0</math>,
-[[Image:Delta_equal_to_0.png|thumb|center|300x300px]]
-====When <math>n=3</math>====
-The discriminant of a polynomial <math>p(x)=ax^3+bx^2+cx+d</math> is given by <math>D(p)=b^2c^2-4b^3d-4ac^3+18abcd-27a^2d^2</math>.
-Also, the compressed cubic form <math>p(z)=z^3+pz+q</math> has discriminant <math>D(p)=-4p^3-27q^2</math>. We can compress a polynomial of degree 3, wich also makes possible to us to use Cardano's formula, by doing the substitution <math>x=z-\frac{a}{3}</math> on the polynomial <math>p(x)=x^3+ax^2+bx+c</math>.
-*If <math>D=0</math>, then at least two of the roots are equal;
-*If <math>D<0</math>, then all three roots are real and distinct;
-*If <math>D>0</math>, then one of the roots is real and the other two are complex conjugate.
-====When <math>n=4</math>====
-The quartic polynomial <math>p(x)=ax^4+bx^3+cx^2+dx+e</math> has discriminant
-<math>D(p)=256a^3e^3-192a^2bde^2-128a^2c^2e^2+144a^2cd^2e-27a^2d^4+144ab^2ce^2-6ab^2d^2e-80abc^2de+18abcd^3+16ac^4e-4ac^3d^2-27b^4e^2+18b^3cde-4b^3d^3-4b^2c^3e+b^2c^2d^2</math>
-*If <math>D=0</math>, then at least two of the roots are equal;
-*If <math>D>0</math>, then the roots are all real or all non-real;
-*If <math>D<0</math>, then there are two real roots and two complex conjugate roots.
-====Some properties====
-For <math>n\geq4</math> we can say that
-*The polynomial has a multiple root if, and only if, <math>D=0</math>;
-*If <math>D>0</math>, with <math>k</math> being a positive integer such that <math>k\geq\frac{n}{4}</math>, with <math>n</math> being the degree of the polynomial, then there are <math>2k</math> pairs of complex conjugate roots  and <math>n-4k</math> real roots;
-*If <math>D<0</math>, with <math>k</math> being a positive integer such that <math>k\geq\frac{n-2}{4}</math>, then there are <math>2k+1</math> pairs of complex conjugate roots and <math>n-4k+2</math> real roots.
-== Example Problems ==
-=== Introductory ===
-* (AMC 12 2005) There are two values of <math>a</math> for which the equation <math>4x^2+ax+8x+9=0</math> has only one solution for <math>x</math>. What is the sum of these values of <math>a</math>?
-Solution: Since we want the <math>a</math>'s where there is only one solution for <math>x</math>, the discriminant has to be <math>0</math>. <math>(a+8)^2-4(4)(9)=a^2+16a-80=0</math>. The sum of these values of <math>a</math> is <math>-16</math>.
-=== Intermediate ===
-* [[1977_Canadian_MO_Problems/Problem_1 | 1977 Canadian MO Problem 1]]
-== Other resources ==
-* [http://en.wikipedia.org/wiki/Discriminant Wikipedia entry]

Page

Toolbox

Search

Difference between revisions of "User:Vqbc/Testing"

Revision as of 22:27, 26 June 2021

Statement

Proof

See also