Difference between revisions of "2020 AMC 12A Problems/Problem 17"
(→Solution 3) |
(→Solution 3) |
||
| Line 23: | Line 23: | ||
| − | < | + | <cmath>[BCDE]=\frac{\ln(n+1)+\ln n}{2}+\frac{\ln(n+2)+\ln(n+1)}{2}+\frac{\ln(n+3)+\ln(n+2)}{2}-\frac{3(\ln(n+3)+\ln n)}{2}</cmath> |
| − | < | + | <cmath>[BCDE]=\tfrac{2\ln(n+1)+2\ln(n+2)-2\ln(n+3)-2\ln n}{2}=\ln(n+1)+\ln(n+2)-\ln(n+3)-\ln n=\ln\tfrac{(n+1)(n+2)}{n(n+3)}</cmath> |
<cmath>\implies\ln\frac{(n+1)(n+2)}{n(n+3)}=\ln\frac{91}{90}\implies \frac{(n+1)(n+2)}{n(n+3)}=\frac{91}{90}</cmath> | <cmath>\implies\ln\frac{(n+1)(n+2)}{n(n+3)}=\ln\frac{91}{90}\implies \frac{(n+1)(n+2)}{n(n+3)}=\frac{91}{90}</cmath> | ||
<cmath>\implies n^2+3n-180=0\implies (n+15)(n-12)=0\implies n=12</cmath> | <cmath>\implies n^2+3n-180=0\implies (n+15)(n-12)=0\implies n=12</cmath> | ||
Revision as of 09:53, 9 March 2020
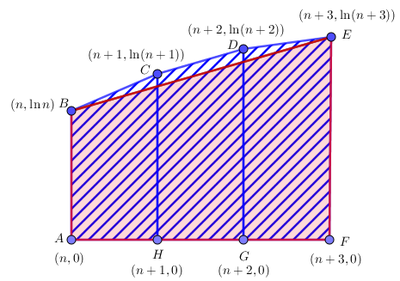
Problem 17
The vertices of a quadrilateral lie on the graph of 
, and the 
-coordinates of these vertices are consecutive positive integers. The area of the quadrilateral is 
. What is the -coordinate of the leftmost vertex?
Solution 1
Let the coordinates of the quadrilateral be 
. We have by shoelace's theorem, that the area is![\[\frac{\ln(n)(n+1) + \ln(n+1)(n+2) + \ln(n+2)(n+3)+n\ln(n+3)}{2} - \frac{\ln(n+1)\ln(n) + \ln(n+2)\ln(n+1) + \ln(n+3)(n+2)+\ln(n)(n+3)}{2}=\]](http://latex.artofproblemsolving.com/d/7/c/d7c3a9dd5365eb0b3ed43de261d00ebee7be223e.png)
![\[\frac{\ln \left( \frac{n^{n+1}(n+1)^{n+2}(n+2)^{n+3}(n+3)^n}{(n+1)^n(n+2)^{n+1}(n+3)^{n+2}n^{n+3}}\right)}{2} = \ln \left( \sqrt{\frac{(n+1)^2(n+3)^2}{n^2(n+2)^2}} \right) = \ln \left(\frac{(n+1)(n+2)}{n(n+3)}\right) = \ln \left( \frac{91}{90} \right).\]](http://latex.artofproblemsolving.com/7/5/a/75afa30306f26c4e3e96ea2bbeec1cdbeedbcb8a.png)
We now that the numerator must have a factor of 
, so given the answer choices, 
is either 
or 
. If 
, the expression 
does not evaluate to 
, but if 
, the expression evaluates to . Hence, our answer is 
.
~AopsUser101
Solution 2
Like above, use the shoelace formula to find that the area of the triangle is equal to 
. Because the final area we are looking for is 
, the numerator factors into and 
, which one of 
and 
has to be a multiple of and the other has to be a multiple of . Clearly, the only choice for that is
~Solution by IronicNinja
Solution 3
How 
is a concave function, then:
Therefore ![$[BCDE]=[ABCH]+[HCDG]+[GDEF]-[ABEF]$](http://latex.artofproblemsolving.com/e/3/9/e399a69e1911bd52b0cb18bd1d32edd4d8a658eb.png)
, all quadrilaterals of side right are trapezius
![\[[BCDE]=\frac{\ln(n+1)+\ln n}{2}+\frac{\ln(n+2)+\ln(n+1)}{2}+\frac{\ln(n+3)+\ln(n+2)}{2}-\frac{3(\ln(n+3)+\ln n)}{2}\]](http://latex.artofproblemsolving.com/6/b/4/6b49d20966d457b29fd23ca11cadd140ef0bb7a1.png)
![\[[BCDE]=\tfrac{2\ln(n+1)+2\ln(n+2)-2\ln(n+3)-2\ln n}{2}=\ln(n+1)+\ln(n+2)-\ln(n+3)-\ln n=\ln\tfrac{(n+1)(n+2)}{n(n+3)}\]](http://latex.artofproblemsolving.com/4/4/b/44b36bdf1379371b54537ebcccecb2d50a137c25.png)
![\[\implies\ln\frac{(n+1)(n+2)}{n(n+3)}=\ln\frac{91}{90}\implies \frac{(n+1)(n+2)}{n(n+3)}=\frac{91}{90}\]](http://latex.artofproblemsolving.com/b/5/4/b54d310717c1635b6e4b92a7cfb00d576864b245.png)
![\[\implies n^2+3n-180=0\implies (n+15)(n-12)=0\implies n=12\]](http://latex.artofproblemsolving.com/1/2/5/125a64661449db0308ff23335f0e46a41c0f00ab.png)
~Solution by AsdrúbalBeltrán
See Also
| 2020 AMC 12A (Problems • Answer Key • Resources) | |
| Preceded by Problem 16 |
Followed by Problem 18 |
| 1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 | |
| All AMC 12 Problems and Solutions | |
The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. 
