Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2004 AMC 12A Problems/Problem 22"

m (Added RISKY SOLUTION)
m (→‎Solution 1)
 
(22 intermediate revisions by 15 users not shown)
Line 2: Line 2:
  
 
== Problem ==
 
== Problem ==
−
<!-- don't remove the following tag, for PoTW on the Wiki front page--><onlyinclude>Three pairwise- [[tangent]] [[sphere]]s of [[radius]] <math>1</math> rest on a horizontal [[plane]]. A sphere of radius <math>2</math> rests on them. What is the [[distance]] from the plane to the top of the larger sphere?<!-- don't remove the following tag, for PoTW on the Wiki front page--></onlyinclude>
+
<!-- don't remove the following tag, for PoTW on the Wiki front page--><onlyinclude>Three mutually tangent spheres of radius <math>1</math> rest on a horizontal plane. A sphere of radius <math>2</math> rests on them. What is the distance from the plane to the top of the larger sphere?<!-- don't remove the following tag, for PoTW on the Wiki front page--></onlyinclude>
  
 
<math>\text {(A)}\ 3 + \frac {\sqrt {30}}{2} \qquad \text {(B)}\ 3 + \frac {\sqrt {69}}{3} \qquad \text {(C)}\ 3 + \frac {\sqrt {123}}{4}\qquad \text {(D)}\ \frac {52}{9}\qquad \text {(E)}\ 3 + 2\sqrt2</math>
 
<math>\text {(A)}\ 3 + \frac {\sqrt {30}}{2} \qquad \text {(B)}\ 3 + \frac {\sqrt {69}}{3} \qquad \text {(C)}\ 3 + \frac {\sqrt {123}}{4}\qquad \text {(D)}\ \frac {52}{9}\qquad \text {(E)}\ 3 + 2\sqrt2</math>
  
 
== Solution 1==
 
== Solution 1==
−
We draw the three spheres of radius <math>1</math>:
 
  
−
[[File:2004AMC12A_22_1_rerender.png]]
+
The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>.  
−
 
 
−
And then add the sphere of radius <math>2</math>:
 
−
 
 
−
[[File:2004AMC12A_22_2_rerender.png]]
 
−
 
 
−
The height from the center of the bottom sphere to the plane is <math>1</math>, and from the center of the top sphere to the tip is <math>2</math>.
 
  
 
[[Image:2004_AMC12A-22a.png]]
 
[[Image:2004_AMC12A-22a.png]]
  
−
We now need the vertical height of the centers. If we connect the centers, we get a triangular [[pyramid]] with an [[equilateral triangle]] base. The distance from the vertex of the equilateral triangle to its [[centroid]] can be found by <math>30-60-90 \triangle</math>s to be <math>\frac{2\sqrt{3}}{3}</math>.
+
We now need the vertical height of the centers. If we connect centers, we get a rectangular [[pyramid]] with an [[equilateral triangle]] base. The distance from the vertex of the equilateral triangle to its [[centroid]] can be found by <math>30\text-60\text-90 \triangle</math>s to be <math>\frac{2\sqrt{3}}{3}</math>.
  
 
[[Image:2004_AMC12A-22b.png]]
 
[[Image:2004_AMC12A-22b.png]]
  
−
By the [[Pythagorean Theorem]], we have <math>\left(\frac{2}{\sqrt{3}}\right)^2 + h^2 = 3^2 \Longrightarrow h = \frac{\sqrt{69}}{3}</math>. Adding the heights up, we get <math>\frac{\sqrt{69}}{3} + 1 + 2 \Rightarrow\boxed{\mathrm{(B)}\ 3+\frac{\sqrt{69}}{3}}</math>
+
By the [[Pythagorean Theorem]], we have <math>\left(\frac{2}{\sqrt{3}}\right)^2 + h^2 = 3^2 \Longrightarrow h = \frac{\sqrt{69}}{3}</math>. Adding the heights up, we get <math>\frac{\sqrt{69}}{3} + 1 + 2 \Rightarrow 3+\frac{\sqrt{69}}{3}, or \boxed{B}</math>
  
 
==Solution 2==
 
==Solution 2==
  
−
Connect the centers of the spheres.  Note that the resulting prism is a tetrahedron with base lengths of 2 and side lengths of 3.  Drop a height from the top of the tetrahedron to the centroid of its equilateral triangle base.  Using the Pythagorean Theorem, it is easy to see that the circumradius of the base is <math> \dfrac { 2 \sqrt {3 } } {3} </math>.  We can use PT again to find the height of the tetrahedron given its base's circumradius and it's leg lengths.  Finally, we add the distance from the top of the tetrahedron to the top of the sphere of radius 2 and the distance from the bottom of the prism to the ground to get an answer of <math>3 + \dfrac{\sqrt{69}}{3}</math>.
+
Connect the centers of the spheres.  Note that the resulting prism is a tetrahedron with base lengths of 2 and side lengths of 3.  Drop a height from the top of the tetrahedron to the centroid of its equilateral triangle base.  Using the Pythagorean Theorem, it is easy to see that the circumradius of the base is <math> \dfrac { 2 \sqrt {3 } } {3} </math>.  We can use PT again to find the height of the tetrahedron given its base's circumradius and it's leg lengths.  Finally, we add the distance from the top of the tetrahedron to the top of the sphere of radius 2 and the distance from the bottom of the prism to the ground to get an answer of <math>\boxed{3 + \dfrac{\sqrt{69}}{3}}</math>.
 +
 
 +
==Video Solution==
 +
https://youtu.be/cHjtoURncoY
  
−
==RISKY, DO NOT TRY UNLESS YOU HAVE NO TIME==
+
~IceMatrix
−
Choice E&A look too simple, so cross them off. Choice C looks too complex, so cross it off. Now, guess between D and B, or just notice that 69 is a fun number, to get B.
 
  
 
== See also ==  
 
== See also ==  

Latest revision as of 20:36, 27 November 2024

The following problem is from both the 2004 AMC 12A #22 and 2004 AMC 10A #25, so both problems redirect to this page.

Problem

Three mutually tangent spheres of radius $1$ rest on a horizontal plane. A sphere of radius $2$ rests on them. What is the distance from the plane to the top of the larger sphere?

$\text {(A)}\ 3 + \frac {\sqrt {30}}{2} \qquad \text {(B)}\ 3 + \frac {\sqrt {69}}{3} \qquad \text {(C)}\ 3 + \frac {\sqrt {123}}{4}\qquad \text {(D)}\ \frac {52}{9}\qquad \text {(E)}\ 3 + 2\sqrt2$

Solution 1

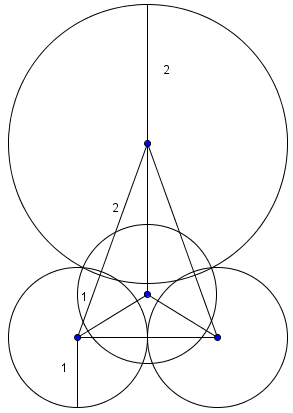
The height from the center of the bottom sphere to the plane is $1$, and from the center of the top sphere to the tip is $2$.

2004 AMC12A-22a.png

We now need the vertical height of the centers. If we connect centers, we get a rectangular pyramid with an equilateral triangle base. The distance from the vertex of the equilateral triangle to its centroid can be found by $30\text-60\text-90 \triangle$s to be $\frac{2\sqrt{3}}{3}$.

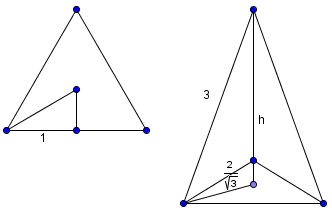
2004 AMC12A-22b.png

By the Pythagorean Theorem, we have $\left(\frac{2}{\sqrt{3}}\right)^2 + h^2 = 3^2 \Longrightarrow h = \frac{\sqrt{69}}{3}$. Adding the heights up, we get $\frac{\sqrt{69}}{3} + 1 + 2 \Rightarrow 3+\frac{\sqrt{69}}{3}, or \boxed{B}$

Solution 2

Connect the centers of the spheres. Note that the resulting prism is a tetrahedron with base lengths of 2 and side lengths of 3. Drop a height from the top of the tetrahedron to the centroid of its equilateral triangle base. Using the Pythagorean Theorem, it is easy to see that the circumradius of the base is $\dfrac { 2 \sqrt {3 } } {3}$. We can use PT again to find the height of the tetrahedron given its base's circumradius and it's leg lengths. Finally, we add the distance from the top of the tetrahedron to the top of the sphere of radius 2 and the distance from the bottom of the prism to the ground to get an answer of $\boxed{3 + \dfrac{\sqrt{69}}{3}}$.

Video Solution

https://youtu.be/cHjtoURncoY

~IceMatrix

See also

2004 AMC 12A (Problems • Answer Key • Resources)
Preceded by
Problem 21 		Followed by
Problem 23
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 12 Problems and Solutions
2004 AMC 10A (Problems • Answer Key • Resources)
Preceded by
Problem 24 		Followed by
Last Question
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2004_AMC_12A_Problems/Problem_22&oldid=235718"