Difference between revisions of "2012 AIME II Problems/Problem 13"

Latest revision as of 17:02, 5 February 2024

Problem 13

Equilateral $\triangle ABC$ has side length $\sqrt{111}$ . There are four distinct triangles $AD_1E_1$ , $AD_1E_2$ , $AD_2E_3$ , and $AD_2E_4$ , each congruent to $\triangle ABC$ , with $BD_1 = BD_2 = \sqrt{11}$ . Find $\sum_{k=1}^4(CE_k)^2$ .

Solution 1

Note that there are only two possible locations for points $D_1$ and $D_2$ , as they are both $\sqrt{111}$ from point $A$ and $\sqrt{11}$ from point $B$ , so they are the two points where a circle centered at $A$ with radius $\sqrt{111}$ and a circle centered at $B$ with radius $\sqrt{11}$ intersect. Let $D_1$ be the point on the opposite side of $\overline{AB}$ from $C$ , and $D_2$ the point on the same side of $\overline{AB}$ as $C$ .

Let $\theta$ be the measure of angle $BAD_1$ (also the measure of angle $BAD_2$ ); by the Law of Cosines, $\begin{align*}\sqrt{11}^2 &= \sqrt{111}^2 + \sqrt{111}^2 - 2 \cdot \sqrt{111} \cdot \sqrt{111} \cdot \cos\theta\\ 11 &= 222(1 - \cos\theta)\end{align*}$

There are two equilateral triangles with $\overline{AD_1}$ as a side; let $E_1$ be the third vertex that is farthest from $C$ , and $E_2$ be the third vertex that is nearest to $C$ .

Angle $E_1AC = E_1AD_1 + D_1AB + BAC = 60 + \theta + 60 = 120 + \theta$ ; by the Law of Cosines, $\begin{align*}(E_1C)^2 &= (E_1A)^2 + (AC)^2 - 2 (E_1A) (AC)\cos(120 + \theta)\\ &= 111 + 111 - 222\cos(120 + \theta)\end{align*}$ Angle $E_2AC = \theta$ ; by the Law of Cosines, $\begin{align*}(E_2C)^2 &= (E_2A)^2 + (AC)^2 - 2 (E_2A) (AC)\cos\theta\\ &= 111 + 111 - 222\,\cos\theta\end{align*}$

There are two equilateral triangles with $\overline{AD_2}$ as a side; let $E_3$ be the third vertex that is farthest from $C$ , and $E_4$ be the third vertex that is nearest to $C$ .

Angle $E_3AC = E_3AB + BAC = (60 - \theta) + 60 = 120 - \theta$ ; by the Law of Cosines, $\begin{align*}(E_3C)^2 &= (E_3A)^2 + (AC)^2 - 2 (E_3A) (AC)\cos(120 - \theta)\\ &= 111 + 111 - 222\cos(120 - \theta)\end{align*}$ Angle $E_4AC = \theta$ ; by the Law of Cosines, $\begin{align*}(E_4C)^2 &= (E_4A)^2 + (AC)^2 - 2 (E_4A) (AC)\cos\theta \\ &= 111 + 111 - 222\cos\theta\end{align*}$

The solution is: $\begin{align*} \sum_{k=1}^4(CE_k)^2 &= (E_1C)^2 + (E_3C)^2 + (E_2C)^2 + (E_4C)^2\\ &= 222(1 - \cos(120 + \theta)) + 222(1 - \cos(120 - \theta)) + 222(1 - \cos\theta) + 222(1 - \cos\theta)\\ &= 222((1 - (\cos120\cos\theta - \sin120\sin\theta)) + (1 - (\cos120\cos\theta + \sin120\sin\theta)) + 2(1 -\cos\theta))\\ &= 222(1 - \cos120\cos\theta + \sin120\sin\theta + 1 - \cos120\cos\theta - \sin120\sin\theta + 2 - 2\cos\theta)\\ &= 222(1 + \frac{1}{2}\cos\theta + 1 + \frac{1}{2}\cos\theta + 2 - 2\cos\theta)\\ &= 222(4 - \cos\theta)\\ &= 666 + 222(1 - \cos\theta) \end{align*}$ Substituting $11$ for $222(1 - \cos\theta)$ gives the solution $666 + 11 = \framebox{677}.$

Solution 2

This problem is pretty much destroyed by complex plane geometry, which is similar to vector geometry only with the power of easy rotation. Place the triangle in the complex plane by letting $C$ be the origin, placing $B$ along the x-axis, and $A$ in the first quadrant. Let $r=\sqrt{111}$ . If $\omega$ denotes the primative sixth root of unity, $e^{i\pi/3}$ , then we have $C=0$ , $B=r$ , and $A=r\omega.$ Recall that counter-clockwise rotation in the complex plane by an angle $\theta$ is accomplished by multiplication by $e^{i\theta}$ (and clockwise rotation is multiplication by its conjugate). So, we can find $D_1$ and $D_2$ by rotating $B$ around $A$ by angles of $\theta$ and $-\theta$ , where $\theta$ is the apex angle in the isoceles triangle with sides $\sqrt{111}$ , $\sqrt{111}$ , and $\sqrt{11}$ . That is, let $z=e^{i\theta}$ , and then:

$D_1=A+z(B-A)$ , and $D_2=A+\overline{z}(B-A)$ . Now notice that $B-A=\overline{A}$ , so this simplifies further to:

$D_1=A+z\overline{A}$ , and $D_2=A+\overline{z}\overline{A}$ .

Similarly, we can write $E_1$ , $E_2$ , $E_3$ , and $E_4$ by rotating $D_1$ and $D_2$ around $A$ by $\pm\pi/3$ :

$E_1=A+\omega(D_1-A)$ , $E_2=A+\overline{\omega}(D_1-A)$ , $E_3=A+\omega(D_2-A)$ , $E_4=A+\overline{\omega}(D_2-A)$ . Thus:

$E_1=A+\omega z \overline{A}$ , $E_2=A+\overline{\omega} z \overline{A}$ , $E_3=A+\omega\overline{z}\overline{A}$ , $E_4=A+\overline{\omega}\overline{z}\overline{A}$ .

Now to find some magnitudes, which is easy since we chose $C$ as the origin:

$\|E_1\|^2=(A+\omega z \overline{A})(\overline{A}+\overline{\omega z}A)=2\|A\|^2+\omega z \overline{A}^2 + \overline{\omega}\overline{z}A^2$ ,

$\|E_2\|^2=(A+\overline{\omega} z \overline{A})(\overline{A}+\omega \overline{z}A)=2\|A\|^2+\overline{\omega} z \overline{A}^2 + \omega\overline{z}A^2$ ,

$\|E_3\|^2=(A+\omega \overline{z} \overline{A})(\overline{A}+\overline{\omega} z A)=2\|A\|^2+\omega \overline{z} \overline{A}^2 + \overline{\omega}zA^2$ ,

$\|E_4\|^2=(A+\overline{\omega z} \overline{A})(\overline{A}+\omega zA)=2\|A\|^2+\overline{\omega z} \overline{A}^2 + \omega zA^2$ .

Adding these up, the sum equals $8\|A\|^2+(\overline{A}^2+A^2)(\omega z + \omega \overline{z} + \overline{\omega}z + \overline{\omega}\overline{z}) = 8\|A\|^2+(\overline{A}^2+A^2)(z + \overline{z})( \omega+ \overline{\omega})$ .

(Isn't that nice?) Notice that $\overline{A}^2+A^2 = r^2(\overline{\omega}^2+\omega^2) = -r^2$ , and $\omega+ \overline{\omega}=1$ , so that this sum simplifies further to $888-111(z + \overline{z})$ .

Finally, $z + \overline{z} = 2\cos{\theta}$ , which is found using the law of cosines on that isoceles triangle: $11=111+111-222\cos{\theta}$ , so $2\cos{\theta}=211/111$ .

Thus, the sum equals $888-211=\framebox{677}$ .

Solution 3

This method uses complex numbers with $A$ as the origin. Let $A=0$ , $B=\sqrt{111}$ , $C = \sqrt{111}\theta$ , where $\theta = e^{i \pi/3} = \frac{1}{2} + \frac{\sqrt{3}}{2}i$ .

Also, let $x$ be $D_1$ or $D_2$ . Then

$|x|=\sqrt{111}, |x-\sqrt{111}|=\sqrt{11}$

Therefore, $11 = |x-\sqrt{111}|^2 = |x|^2 + 111 -2\sqrt{111}Re(x) = 222 - 2\sqrt{111}Re(x)$ , so

$2\sqrt{111}Re(x) = 211.$

Since $E_1$ , $E_2$ are one of $D_1\theta$ or $D_1\theta^{-1}$ , without loss of generality, let $E_1=D_1\theta$ and $E_2 = D_1\theta^{-1}$ . Then

$|CE_1|^2 = |\sqrt{111}-D_1|^2 = |\sqrt{111}-x|^2=11$ $|CE_2|^2 = |\theta^2 \sqrt{111} - D_1|^2 = 222-2\sqrt{111} Re(D_1 \theta^2)$

One can similarly get $|CE_3|=11$ and $|CE_4|=222-2\sqrt{111} Re(D_2 \theta^2)$ , so the desired sum is equal to

$22+444-2\sqrt{111}(Re(D_1 \theta^2)+Re(D_1 \theta^2))$

Note that $Re(D_{1,2} \theta^2) = Re((Re(x) \pm Im(x)i)(-1/2 + \sqrt{3}/2i)) = - (Re(x)/2 \pm Im(x)\sqrt{3}/2)$ , so the sum of these two is just $-Re(x)$ . Therefore the desired sum is equal to

$22+444+2\sqrt{111}Re(x) = 22+444+211 = \framebox{677}.$

Solution 4

This method uses the observation that every point is equidistant from $A$ . Without loss of generality, we can assume $C$ is on the same side of $AB$ as $D_1$ .

We can start off by angle chasing the angles around $A$ . We let $\angle BAD_1 = \alpha$ . Then, we note that $BD_1 = BD_2$ and $AD_1 = AB = AD_2$ . Thus, $\bigtriangleup ABD_1 \cong \bigtriangleup ABD_2$ . Thus, $\angle BAD_2 = \alpha$ also.

We can now angle chase the angles about $A$ . Because $\angle D_2AE_3 = 60$ , $\angle D_1AE_3 = 60- 2 \alpha$ . We can use all the congruent equilateral triangles in a similar manner obtaining: $\angle D_1AE_3 = 60- 2 \alpha$ $\angle E_3AC = \alpha$ $\angle CAE_1 = \alpha$ $\angle D_2AE_2 = 60- 2 \alpha$ $\angle E_2AE_4 = 2 \alpha$

Now, $AE_3 = AC = \sqrt{111}$ and $\angle E_3AC = \alpha$ . Thus, $\bigtriangleup E_3AC \cong \bigtriangleup BAD_1$ . Thus, $CE_3^2 = BD_1^2 = 11$ .

Similarly, $AC = AE_1 = \sqrt{111}$ and $\angle CAE_1 = \alpha$ . Thus, $\bigtriangleup CAE_1 \cong \bigtriangleup BAD_1$ . Thus, $CE_1^2 = BD_1^2 = 11$ .

We can use $\bigtriangleup CAE_2$ to find $CE_2^2$ . Law of Cosines yields $CE_2^2 = AE_2^2 + AC^2 - 2 \cdot AE_2 \cdot AC \cdot \cos(\angle E_2AC).$ Substituting the known lengths and angles gives $CE_2^2 = 222 - 222 \cdot \cos(120- \alpha).$ Expanding this with the Cosine Subtraction Identity we get $CE_2^2 = 222 - 222(\cos120 \cos \alpha + \sin120 \sin \alpha).$

We could attempt to calculate this but we can clear it up by simultaneously finding $CE_4^2$ too. We use Law of Cosines on $\bigtriangleup CAE_4$ to get $CE_4^2 = AE_4^2 + AC^2 - 2 \cdot AE_4 \cdot AC \cdot \cos(\angle E_4AC).$ Substituting the known lengths and angles gives $CE_4^2 = 222 - 222 \cdot \cos(120 + \alpha).$ Expanding this with the Cosine Addition Identity we get $CE_4^2 = 222 - 222(\cos120 \cos \alpha - \sin120 \sin \alpha).$ Adding this to our equation for $CE_2^2$ , we get $CE_2^2 + CE_4^2 = 444 - 222(\cos120 \cos \alpha - \sin120 \sin \alpha) - 222(\cos120 \cos \alpha + \sin120 \sin \alpha).$ Simplifying we get $CE_2^2 + CE_4^2 = 444 - 444(\cos120 \cos \alpha)$

We can find $\cos \alpha$ by using Law of Cosines on $\bigtriangleup BAD_1$ . This gives $11 = 222 - 222 \cos \alpha.$ Thus $\cos \alpha = \frac{211}{222}$ . Substituting it in gives $CE_2^2 + CE_4^2 = 444 - 444(\cos120 \cdot \frac{211}{222}).$ Thus $CE_2^2 + CE_4^2 = 444 + 211 = 655.$

Therefore the desired sum is equal to

$11+11+655 = \framebox{677}.$

Solution 5

We create a diagram. Each of the red quadrilaterals are actually 60 degree rotations about point A. We easily get that $\overline{C E_1} = \sqrt{11}$ , and $\overline{C E_3} = \sqrt{11}$ . If we set $\angle B A D_2 = \theta$ , we can start angle chasing. In particular, we will like to find $\angle D E_4 C$ , and $\angle D E_2 C$ , since then we will be able to set up some Law Of Cosines. $\angle D E_4 C = \angle D E_4 A + \angle A E_4 C = 90 - \frac{\theta}{2} + 30 + \frac{\theta}{2} = 120^{\circ}$ That was convenient! We can do it with the other angle as well. $\angle D E_2 C = \angle D E_2 A - \angle C E_2 A = 90 - \frac{\theta}{2} - (30 - \frac{\theta}{2}) = 60^{\circ}$ . That means we are able to set up Law of Cosines, on triangles $\triangle D E_4 C$ and $\triangle D E_2 C$ , with some really convenient angles. Let $CE_2 = x$ , and $CE_4 = y$ . $333 = 11 + x^2 - \sqrt{11} x$ $333 = 11 + y^2 + \sqrt{11} y$ We subtract and get: $0 = (x+y)(x-y-\sqrt{11})$ $x+y$ obviously can't be 0, so $x-y = \sqrt{11}$ We add and get: $666 = 22 + x^2 + y^2 + \sqrt{11} (y-x)$ . $y-x = -\sqrt{11}$ . Thus, we can fill in and solve. $666 = 22 + x^2 + y^2 - 11$ $655 = x^2 + y^2$ Thus our answer is $C E_1^2 + C E_2^2 + C E_2^2 + C E_4^2 = 11 + 11 + C E_2^2 + C E_4^2 = 11 + 11 + x^2 + y^2 = 11 + 11 + 655 = \boxed{677}$ .

-Alexlikemath

Video Solution by MOP 2024

https://youtu.be/IUOqCEGgG0g

~r00tsOfUnity

@@ Line 1: / Line 1: @@
-==Problem==
 == Problem 13 ==
 Equilateral <math>\triangle ABC</math> has side length <math>\sqrt{111}</math>. There are four distinct triangles <math>AD_1E_1</math>, <math>AD_1E_2</math>, <math>AD_2E_3</math>, and <math>AD_2E_4</math>, each congruent to <math>\triangle ABC</math>,
 with <math>BD_1 = BD_2 = \sqrt{11}</math>. Find <math>\sum_{k=1}^4(CE_k)^2</math>.
 == Solution 1 ==
@@ Line 16: / Line 13: @@
 Angle <math>E_1AC = E_1AD_1 + D_1AB + BAC = 60 + \theta + 60 = 120 + \theta</math>; by the Law of Cosines,
-<cmath>\begin{align*}(E_1C)^2 &= (E_1A)^2 + (AC)^2 - 2 (E_1A) (E_1C)\cos(120 + \theta)\\
+<cmath>\begin{align*}(E_1C)^2 &= (E_1A)^2 + (AC)^2 - 2 (E_1A) (AC)\cos(120 + \theta)\\
 &= 111 + 111 - 222\cos(120 + \theta)\end{align*}</cmath>
 Angle <math>E_2AC = \theta</math>; by the Law of Cosines,
-<cmath>\begin{align*}(E_2C)^2 &= (E_2A)^2 + (AC)^2 - 2 (E_2A) (E_2C)\cos\theta\\
+<cmath>\begin{align*}(E_2C)^2 &= (E_2A)^2 + (AC)^2 - 2 (E_2A) (AC)\cos\theta\\
 &= 111 + 111 - 222\,\cos\theta\end{align*}</cmath>
@@ Line 25: / Line 22: @@
 Angle <math>E_3AC = E_3AB + BAC = (60 - \theta) + 60 = 120 - \theta</math>; by the Law of Cosines,
-<cmath>\begin{align*}(E_3C)^2 &= (E_3A)^2 + (AC)^2 - 2 (E_3A) (E_3C)\cos(120 - \theta)\\
+<cmath>\begin{align*}(E_3C)^2 &= (E_3A)^2 + (AC)^2 - 2 (E_3A) (AC)\cos(120 - \theta)\\
 &= 111 + 111 - 222\cos(120 - \theta)\end{align*}</cmath>
 Angle <math>E_4AC = \theta</math>; by the Law of Cosines,
-<cmath>\begin{align*}(E_4C)^2 &= (E_4A)^2 + (AC)^2 - 2 (E_4A) (E_4C)\cos\theta \\
+<cmath>\begin{align*}(E_4C)^2 &= (E_4A)^2 + (AC)^2 - 2 (E_4A) (AC)\cos\theta \\
 &= 111 + 111 - 222\cos\theta\end{align*}</cmath>
@@ Line 44: / Line 41: @@
 == Solution 2 ==
-This problem is pretty much destroyed by complex plane geometry, which is similar to vector geometry only with the power of easy rotation.  Place the triangle in the complex plane by letting <math>C</math> be the origin, placing <math>B</math> along the x-axis, and <math>A</math> in the first quadrant.  Let <math>r=\sqrt{111}</math>.  If <math>\omega</math> denotes the sixth root of unity, <math>e^{i\pi/3}</math>, then we have <math>C=0</math>, <math>B=r</math>, and <math>A=r\omega.</math>  Recall that counter-clockwise rotation in the complex plane by an angle <math>\theta</math> is accomplished by multiplication by <math>e^{i\theta}</math> (and clockwise rotation is multiplication by its conjugate).  So, we can find <math>D_1</math> and <math>D_2</math> by rotating <math>B</math> around <math>A</math> by angles of <math>\theta</math> and <math>-\theta</math>, where <math>\theta</math> is the apex angle in the isoceles triangle with sides <math>\sqrt{111}</math>, <math>\sqrt{111}</math>, and <math>\sqrt{11}</math>.  That is, let <math>z=e^{i\theta}</math>, and then:
+This problem is pretty much destroyed by complex plane geometry, which is similar to vector geometry only with the power of easy rotation.  Place the triangle in the complex plane by letting <math>C</math> be the origin, placing <math>B</math> along the x-axis, and <math>A</math> in the first quadrant.  Let <math>r=\sqrt{111}</math>.  If <math>\omega</math> denotes the primative sixth root of unity, <math>e^{i\pi/3}</math>, then we have <math>C=0</math>, <math>B=r</math>, and <math>A=r\omega.</math>  Recall that counter-clockwise rotation in the complex plane by an angle <math>\theta</math> is accomplished by multiplication by <math>e^{i\theta}</math> (and clockwise rotation is multiplication by its conjugate).  So, we can find <math>D_1</math> and <math>D_2</math> by rotating <math>B</math> around <math>A</math> by angles of <math>\theta</math> and <math>-\theta</math>, where <math>\theta</math> is the apex angle in the isoceles triangle with sides <math>\sqrt{111}</math>, <math>\sqrt{111}</math>, and <math>\sqrt{11}</math>.  That is, let <math>z=e^{i\theta}</math>, and then:
 <math>D_1=A+z(B-A)</math>, and <math>D_2=A+\overline{z}(B-A)</math>.  Now notice that <math>B-A=\overline{A}</math>, so this simplifies further to:
@@ Line 144: / Line 141: @@
 <cmath>11+11+655 = \framebox{677}.</cmath>
+== Solution 5 ==
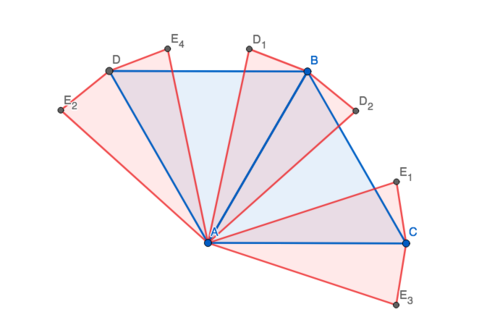
+[[Image:Screen Shot 2020-02-17 at 2.24.50 PM.png|500px]]
+We create a diagram. Each of the red quadrilaterals are actually 60 degree rotations about point A. We easily get that <math>\overline{C E_1} = \sqrt{11}</math>, and <math> \overline{C E_3} = \sqrt{11}</math>. If we set <math>\angle B A D_2 = \theta</math>, we can start angle chasing. In particular, we will like to find <math>\angle D E_4 C</math>, and <math>\angle D E_2 C</math>, since then we will be able to set up some Law Of Cosines. <math>\angle D E_4 C = \angle D E_4 A + \angle A E_4 C = 90 - \frac{\theta}{2} + 30 + \frac{\theta}{2} = 120^{\circ}</math> That was convenient! We can do it with the other angle as well. <math>\angle D E_2 C = \angle D E_2 A - \angle C E_2 A = 90 - \frac{\theta}{2} - (30 - \frac{\theta}{2}) = 60^{\circ}</math>. That means we are able to set up Law of Cosines, on triangles <math>\triangle D E_4 C</math> and <math>\triangle D E_2 C</math>, with some really convenient angles.
+Let <math>CE_2 = x</math>, and <math>CE_4 = y</math>.
+<cmath>333 = 11 + x^2 - \sqrt{11} x</cmath>
+<cmath>333 = 11 + y^2 + \sqrt{11} y</cmath>
+We subtract and get:
+<cmath>0 = (x+y)(x-y-\sqrt{11})</cmath>
+<math>x+y</math> obviously can't be 0, so <math>x-y = \sqrt{11}</math>
+We add and get:
+<cmath>666 = 22 + x^2 + y^2 + \sqrt{11} (y-x)</cmath>.
+<math>y-x = -\sqrt{11}</math>. Thus, we can fill in and solve.
+<cmath>666 = 22 + x^2 + y^2 - 11</cmath>
+<cmath>655 = x^2 + y^2</cmath>
+Thus our answer is <math>C E_1^2 + C E_2^2 + C E_2^2 + C E_4^2 = 11 + 11 + C E_2^2 + C E_4^2 = 11 + 11 + x^2 + y^2 = 11 + 11 + 655 = \boxed{677}</math>.
+-Alexlikemath
+==Video Solution by MOP 2024==
+https://youtu.be/IUOqCEGgG0g
+~r00tsOfUnity
 == See Also ==
 {{AIME box|year=2012|n=II|num-b=12|num-a=14}}
+[[Category:Intermediate Geometry Problems]]
 {{MAA Notice}}

2012 AIME II (Problems • Answer Key • Resources)
Preceded by Problem 12	Followed by Problem 14
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

Page

Toolbox

Search