Difference between revisions of "1983 AHSME Problems"

Latest revision as of 22:43, 2 December 2021

1983 AHSME (Answer Key) Printable versions: Wiki • AoPS Resources • PDF
Instructions This is a 30-question, multiple choice test. Each question is followed by answers marked A, B, C, D and E. Only one of these is correct. You will receive 5 points for each correct answer, 2 points for each problem left unanswered, and 0 points for each incorrect answer. No aids are permitted other than scratch paper, graph paper, ruler, compass, protractor and erasers. Figures are not necessarily drawn to scale. You will have 90 minutes working time to complete the test.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30

Problem 1

If $x \neq 0, \frac x{2} = y^2$ and $\frac{x}{4} = 4y$ , then $x$ equals

$\textbf{(A)}\ 8\qquad \textbf{(B)}\ 16\qquad \textbf{(C)}\ 32\qquad \textbf{(D)}\ 64\qquad \textbf{(E)}\ 128$

Solution

Problem 2

Point $P$ is outside circle $C$ on the plane. At most how many points on $C$ are $3$ cm from P?

$\textbf{(A)} \ 1 \qquad \textbf{(B)} \ 2 \qquad \textbf{(C)} \ 3 \qquad \textbf{(D)} \ 4 \qquad \textbf{(E)} \ 8$

Solution

Problem 3

Three primes $p,q$ and $r$ satisfy $p+q = r$ and $1 < p < q$ . Then $p$ equals

$\textbf{(A)}\ 2\qquad \textbf{(B)}\ 3\qquad \textbf{(C)}\ 7\qquad \textbf{(D)}\ 13\qquad \textbf{(E)}\ 17$

Solution

Problem 4

In the adjoining plane figure, sides $AF$ and $CD$ are parallel, as are sides $AB$ and $EF$ , and sides $BC$ and $ED$ . Each side has length $1$ . Also, $\angle FAB = \angle BCD = 60^\circ$ . The area of the figure is

$\textbf{(A)} \ \frac{\sqrt 3}{2} \qquad \textbf{(B)} \ 1 \qquad \textbf{(C)} \ \frac{3}{2} \qquad \textbf{(D)}\ \sqrt{3}\qquad \textbf{(E)}\ 2$

Solution

Problem 5

Triangle $ABC$ has a right angle at $C$ . If $\sin A = \frac{2}{3}$ , then $\tan B$ is

$\textbf{(A)}\ \frac{3}{5}\qquad \textbf{(B)}\ \frac{\sqrt 5}{3}\qquad \textbf{(C)}\ \frac{2}{\sqrt 5}\qquad \textbf{(D)}\ \frac{\sqrt{5}}{2}\qquad \textbf{(E)}\ \frac{5}{3}$

Solution

Problem 6

When $x^5, x+\frac{1}{x}$ and $1+\frac{2}{x} + \frac{3}{x^2}$ are multiplied, the product is a polynomial of degree

$\textbf{(A)}\ 2\qquad \textbf{(B)}\ 3\qquad \textbf{(C)}\ 6\qquad \textbf{(D)}\ 7\qquad \textbf{(E)}\ 8$

Solution

Problem 7

Alice sells an item at $$10$ less than the list price and receives $10\%$ of her selling price as her commission. Bob sells the same item at $$20$ less than the list price and receives $20\%$ of his selling price as his commission. If they both get the same commission, then the list price is

$\textbf{(A) } $20\qquad \textbf{(B) } $30\qquad \textbf{(C) } $50\qquad \textbf{(D) } $70\qquad \textbf{(E) } $100$

Solution

Problem 8

Let $f(x) = \frac{x+1}{x-1}$ . Then for $x^2 \neq 1, f(-x)$ is

$\textbf{(A)}\ \frac{1}{f(x)}\qquad \textbf{(B)}\ -f(x)\qquad \textbf{(C)}\ \frac{1}{f(-x)}\qquad \textbf{(D)}\ -f(-x)\qquad \textbf{(E)}\ f(x)$

Solution

Problem 9

In a certain population the ratio of the number of women to the number of men is $11$ to $10$ . If the average (arithmetic mean) age of the women is $34$ and the average age of the men is $32$ , then the average age of the population is

$\textbf{(A)}\ 32\frac{9}{10}\qquad \textbf{(B)}\ 32\frac{20}{21}\qquad \textbf{(C)}\ 33\qquad \textbf{(D)}\ 33\frac{1}{21}\qquad \textbf{(E)}\ 33\frac{1}{10}$

Solution

Problem 10

Segment $AB$ is both a diameter of a circle of radius $1$ and a side of an equilateral triangle $ABC$ . The circle also intersects $AC$ and $BC$ at points $D$ and $E$ , respectively. The length of $AE$ is

$\textbf{(A)} \ \frac{3}{2} \qquad \textbf{(B)} \ \frac{5}{3} \qquad \textbf{(C)} \ \frac{\sqrt 3}{2} \qquad \textbf{(D)}\ \sqrt{3}\qquad \textbf{(E)}\ \frac{2+\sqrt 3}{2}$

Solution

Problem 11

Simplify $\sin (x-y) \cos y + \cos (x-y) \sin y$ .

$\textbf{(A)}\ 1\qquad \textbf{(B)}\ \sin x\qquad \textbf{(C)}\ \cos x\qquad \textbf{(D)}\ \sin x \cos 2y\qquad \textbf{(E)}\ \cos x\cos 2y$

Solution

Problem 12

If $\log_7 \Big(\log_3 (\log_2 x) \Big) = 0$ , then $x^{-1/2}$ equals

$\textbf{(A)} \ \frac{1}{3} \qquad \textbf{(B)} \ \frac{1}{2 \sqrt 3} \qquad \textbf{(C)}\ \frac{1}{3\sqrt 3}\qquad \textbf{(D)}\ \frac{1}{\sqrt{42}}\qquad \textbf{(E)}\ \text{none of these}$

Solution

Problem 13

If $xy = a, xz =b,$ and $yz = c$ , and none of these quantities is $0$ , then $x^2+y^2+z^2$ equals

$\textbf{(A)}\ \frac{ab+ac+bc}{abc}\qquad \textbf{(B)}\ \frac{a^2+b^2+c^2}{abc}\qquad \textbf{(C)}\ \frac{(a+b+c)^2}{abc}\qquad \textbf{(D)}\ \frac{(ab+ac+bc)^2}{abc}\qquad \textbf{(E)}\ \frac{(ab)^2+(ac)^2+(bc)^2}{abc}$

Solution

Problem 14

The units digit of $3^{1001} 7^{1002} 13^{1003}$ is

$\textbf{(A)}\ 1\qquad \textbf{(B)}\ 3\qquad \textbf{(C)}\ 5\qquad \textbf{(D)}\ 7\qquad \textbf{(E)}\ 9$

Solution

Problem 15

Three balls marked $1,2$ and $3$ are placed in an urn. One ball is drawn, its number is recorded, and then the ball is returned to the urn. This process is repeated and then repeated once more, and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is $6$ , what is the probability that the ball numbered $2$ was drawn all three times?

$\textbf{(A)} \ \frac{1}{27} \qquad \textbf{(B)} \ \frac{1}{8} \qquad \textbf{(C)} \ \frac{1}{7} \qquad \textbf{(D)} \ \frac{1}{6} \qquad \textbf{(E)}\ \frac{1}{3}$

Solution

Problem 16

Let $x = .123456789101112....998999$ , where the digits are obtained by writing the integers $1$ through $999$ in order. The $1983$ ^rd digit to the right of the decimal point is

$\textbf{(A)}\ 2\qquad \textbf{(B)}\ 3\qquad \textbf{(C)}\ 5\qquad \textbf{(D)}\ 7\qquad \textbf{(E)}\ 8$

Solution

Problem 17

The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin. One of these numbers is the reciprocal of $F$ . Which one?

$\textbf{(A)} \ A \qquad \textbf{(B)} \ B \qquad \textbf{(C)} \ C \qquad \textbf{(D)} \ D \qquad \textbf{(E)} \ E$

Solution

Problem 18

Let $f$ be a polynomial function such that, for all real $x$ , $f(x^2 + 1) = x^4 + 5x^2 + 3$ . For all real $x, f(x^2-1)$ is

$\textbf{(A)}\ x^4+5x^2+1\qquad \textbf{(B)}\ x^4+x^2-3\qquad \textbf{(C)}\ x^4-5x^2+1\qquad \textbf{(D)}\ x^4+x^2+3\qquad \textbf{(E)}\ \text{none of these}$

Solution

Problem 19

Point $D$ is on side $CB$ of triangle $ABC$ . If $\angle{CAD} = \angle{DAB} = 60^\circ\mbox{, }AC = 3\mbox{ and }AB = 6$ , then the length of $AD$ is

$\textbf{(A)} \ 2 \qquad \textbf{(B)} \ 2.5 \qquad \textbf{(C)} \ 3 \qquad \textbf{(D)} \ 3.5 \qquad \textbf{(E)} \ 4$

Solution

Problem 20

If $\tan{\alpha}$ and $\tan{\beta}$ are the roots of $x^2 - px + q = 0$ , and $\cot{\alpha}$ and $\cot{\beta}$ are the roots of $x^2 - rx + s = 0$ , then $rs$ is necessarily

$\textbf{(A)} \ pq \qquad \textbf{(B)} \ \frac{1}{pq} \qquad \textbf{(C)} \ \frac{p}{q^2} \qquad \textbf{(D)}\ \frac{q}{p^2}\qquad \textbf{(E)}\ \frac{p}{q}$

Solution

Problem 21

Find the smallest positive number from the numbers below.

$\textbf{(A)} \ 10-3\sqrt{11} \qquad \textbf{(B)} \ 3\sqrt{11}-10 \qquad \textbf{(C)}\ 18-5\sqrt{13}\qquad \textbf{(D)}\ 51-10\sqrt{26}\qquad \textbf{(E)}\ 10\sqrt{26}-51$

Solution

Problem 22

Consider the two functions $f(x) = x^2+2bx+1$ and $g(x) = 2a(x+b)$ , where the variable $x$ and the constants $a$ and $b$ are real numbers. Each such pair of constants $a$ and $b$ may be considered as a point $(a,b)$ in an $ab$ -plane. Let $S$ be the set of such points $(a,b)$ for which the graphs of $y = f(x)$ and $y = g(x)$ do not intersect (in the $xy$ -plane). The area of $S$ is

$\textbf{(A)} \ 1 \qquad \textbf{(B)} \ \pi \qquad \textbf{(C)} \ 4 \qquad \textbf{(D)} \ 4 \pi \qquad \textbf{(E)} \ \text{infinite}$

Solution

Problem 23

In the adjoining figure the five circles are tangent to one another consecutively and to the lines $L_1$ and $L_2$ . If the radius of the largest circle is $18$ and that of the smallest one is $8$ , then the radius of the middle circle is

$[asy] size(250);defaultpen(linewidth(0.7)); real alpha=5.797939254, x=71.191836; int i; for(i=0; i<5; i=i+1) { real r=8*(sqrt(6)/2)^i; draw(Circle((x+r)*dir(alpha), r)); x=x+2r; } real x=71.191836+40+20*sqrt(6), r=18; pair A=tangent(origin, (x+r)*dir(alpha), r, 1), B=tangent(origin, (x+r)*dir(alpha), r, 2); pair A1=300*dir(origin--A), B1=300*dir(origin--B); draw(B1--origin--A1); pair X=(69,-5), X1=reflect(origin, (x+r)*dir(alpha))*X, Y=(200,-5), Y1=reflect(origin, (x+r)*dir(alpha))*Y, Z=(130,0), Z1=reflect(origin, (x+r)*dir(alpha))*Z; clip(X--Y--Y1--X1--cycle); label("$L_2$", Z, S); label("$L_1$", Z1, dir(2*alpha)*dir(90));[/asy]$

$\textbf{(A)} \ 12 \qquad \textbf{(B)} \ 12.5 \qquad \textbf{(C)} \ 13 \qquad \textbf{(D)} \ 13.5 \qquad \textbf{(E)} \ 14$

Solution

Problem 24

How many non-congruent right triangles are there such that the perimeter in $\text{cm}$ and the area in $\text{cm}^2$ are numerically equal?

$\textbf{(A)} \ \text{none} \qquad \textbf{(B)} \ 1 \qquad \textbf{(C)} \ 2 \qquad \textbf{(D)} \ 4 \qquad \textbf{(E)} \ \text{infinitely many}$

Solution

Problem 25

If $60^a = 3$ and $60^b = 5$ , then $12^{(1-a-b)/\left(2\left(1-b\right)\right)}$ is

$\textbf{(A)} \ \sqrt{3} \qquad \textbf{(B)} \ 2 \qquad \textbf{(C)} \ \sqrt{5} \qquad \textbf{(D)} \ 3 \qquad \textbf{(E)} \ \sqrt{12}$

Solution

Problem 26

The probability that event $A$ occurs is $\frac{3}{4}$ ; the probability that event B occurs is $\frac{2}{3}$ . Let $p$ be the probability that both $A$ and $B$ occur. The smallest interval necessarily containing $p$ is the interval

$\textbf{(A)}\ \Big[\frac{1}{12},\frac{1}{2}\Big]\qquad \textbf{(B)}\ \Big[\frac{5}{12},\frac{1}{2}\Big]\qquad \textbf{(C)}\ \Big[\frac{1}{2},\frac{2}{3}\Big]\qquad \textbf{(D)}\ \Big[\frac{5}{12},\frac{2}{3}\Big]\qquad \textbf{(E)}\ \Big[\frac{1}{12},\frac{2}{3}\Big]$

Solution

Problem 27

A large sphere is on a horizontal field on a sunny day. At a certain time the shadow of the sphere reaches out a distance of $10$ m from the point where the sphere touches the ground. At the same instant a meter stick (held vertically with one end on the ground) casts a shadow of length $2$ m. What is the radius of the sphere in meters? (Assume the sun's rays are parallel and the meter stick is a line segment.)

$\textbf{(A)}\ \frac{5}{2}\qquad \textbf{(B)}\ 9 - 4\sqrt{5}\qquad \textbf{(C)}\ 8\sqrt{10} - 23\qquad \textbf{(D)}\ 6-\sqrt{15}\qquad \textbf{(E)}\ 10\sqrt{5}-20$

Solution

Problem 28

Triangle $\triangle ABC$ in the figure has area $10$ . Points $D, E$ and $F$ , all distinct from $A, B$ and $C$ , are on sides $AB, BC$ and $CA$ respectively, and $AD = 2, DB = 3$ . If triangle $\triangle ABE$ and quadrilateral $DBEF$ have equal areas, then that area is

$[asy] defaultpen(linewidth(0.7)+fontsize(10)); pair A=origin, B=(10,0), C=(8,7), F=7*dir(A--C), E=(10,0)+4*dir(B--C), D=4*dir(A--B); draw(A--B--C--A--E--F--D); pair point=incenter(A,B,C); label("$A$", A, dir(point--A)); label("$B$", B, dir(point--B)); label("$C$", C, dir(point--C)); label("$D$", D, dir(point--D)); label("$E$", E, dir(point--E)); label("$F$", F, dir(point--F)); label("$2$", (2,0), S); label("$3$", (7,0), S);[/asy]$

$\textbf{(A)}\ 4\qquad \textbf{(B)}\ 5\qquad \textbf{(C)}\ 6\qquad \textbf{(D)}\ \frac{5}{3}\sqrt{10}\qquad \textbf{(E)}\ \text{not uniquely determined}$

Solution

Problem 29

A point $P$ lies in the same plane as a given square of side $1$ . Let the vertices of the square, taken counterclockwise, be $A, B, C$ and $D$ . Also, let the distances from $P$ to $A, B$ and $C$ , respectively, be $u, v$ and $w$ . What is the greatest distance that $P$ can be from $D$ if $u^2 + v^2 = w^2$ ?

$\textbf{(A)}\ 1 + \sqrt{2}\qquad \textbf{(B)}\ 2\sqrt{2}\qquad \textbf{(C)}\ 2 + \sqrt{2}\qquad \textbf{(D)}\ 3\sqrt{2}\qquad \textbf{(E)}\ 3+\sqrt{2}$

Solution

Problem 30

Distinct points $A$ and $B$ are on a semicircle with diameter $MN$ and center $C$ . The point $P$ is on $CN$ and $\angle CAP = \angle CBP = 10^{\circ}$ . If $\stackrel{\frown}{MA} = 40^{\circ}$ , then $\stackrel{\frown}{BN}$ equals

$[asy] import geometry; import graph; unitsize(2 cm); pair A, B, C, M, N, P; M = (-1,0); N = (1,0); C = (0,0); A = dir(140); B = dir(20); P = extension(A, A + rotate(10)*(C - A), B, B + rotate(10)*(C - B)); draw(M--N); draw(arc(C,1,0,180)); draw(A--C--B); draw(A--P--B); label("$A$", A, NW); label("$B$", B, E); label("$C$", C, S); label("$M$", M, SW); label("$N$", N, SE); label("$P$", P, S); [/asy]$

$\textbf{(A)}\ 10^{\circ}\qquad \textbf{(B)}\ 15^{\circ}\qquad \textbf{(C)}\ 20^{\circ}\qquad \textbf{(D)}\ 25^{\circ}\qquad \textbf{(E)}\ 30^{\circ}$

Solution

1983 AHSME (Problems • Answer Key • Resources)
Preceded by 1982 AHSME	Followed by 1984 AHSME
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30
All AHSME Problems and Solutions

Page

Toolbox

Search

Difference between revisions of "1983 AHSME Problems"

Latest revision as of 22:43, 2 December 2021

Contents

Problem 1

Problem 2

Problem 3

Problem 4

Problem 5

Problem 6

Problem 7

Problem 8

Problem 9

Problem 10

Problem 11

Problem 12

Problem 13

Problem 14

Problem 15

Problem 16

Problem 17

Problem 18

Problem 19

Problem 20

Problem 21

Problem 22

Problem 23

Problem 24

Problem 25

Problem 26

Problem 27

Problem 28

Problem 29

Problem 30

See also

@@ Line 1: / Line 1: @@
+{{AHSME Problems
+|year = 1983
+}}
 == Problem 1 ==
@@ Line 13: / Line 16: @@
 == Problem 2 ==
-Point <math>P</math> is outside circle <math>C</math> on the plane. At most how many points on <math>C</math> are <math>3 \text{cm}</math> from P?
+Point <math>P</math> is outside circle <math>C</math> on the plane. At most how many points on <math>C</math> are <math>3</math> cm from P?
-<math>\text{(A)} \ 1 \qquad
+<math>\textbf{(A)} \ 1 \qquad
-\text{(B)} \ 2 \qquad
+\textbf{(B)} \ 2 \qquad
-\text{(C)} \ 3 \qquad
+\textbf{(C)} \ 3 \qquad
-\text{(D)} \ 4 \qquad
+\textbf{(D)} \ 4 \qquad
-\text{(E)} \ 8  </math>
+\textbf{(E)} \ 8  </math>
 [[1983 AHSME Problems/Problem 2|Solution]]
@@ Line 25: / Line 28: @@
 == Problem 3 ==
-Three primes <math>p,q</math>, and <math>r</math> satisfy <math>p+q = r</math> and <math>1 < p < q</math>. Then <math>p</math> equals
+Three primes <math>p,q</math> and <math>r</math> satisfy <math>p+q = r</math> and <math>1 < p < q</math>. Then <math>p</math> equals
 <math>\textbf{(A)}\ 2\qquad
@@ Line 37: / Line 40: @@
 == Problem 4 ==
-Position <math>A,B,C,D,E,F</math> such that <math>AF</math> and <math>CD</math> are parallel, as are sides <math>AB</math> and <math>EF</math>,
+[[File:pdfresizer.com-pdf-convert.png]]
-and sides <math>BC</math> and <math>ED</math>. Each side has length of <math>1</math> and it is given that <math>\measuredangle FAB = \measuredangle BCD = 60^\circ</math>.
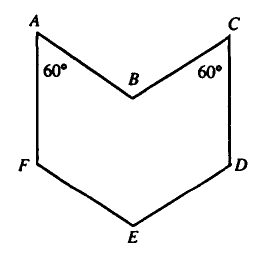
+In the adjoining plane figure, sides <math>AF</math> and <math>CD</math> are parallel, as are sides <math>AB</math> and <math>EF</math>,
+and sides <math>BC</math> and <math>ED</math>. Each side has length <math>1</math>. Also, <math>\angle FAB = \angle BCD = 60^\circ</math>.
 The area of the figure is
 <math>
-\text{(A)} \ \frac{\sqrt 3}{2} \qquad
+\textbf{(A)} \ \frac{\sqrt 3}{2} \qquad
-\text{(B)} \ 1 \qquad
+\textbf{(B)} \ 1 \qquad
-\text{(C)} \ \frac{3}{2} \qquad
+\textbf{(C)} \ \frac{3}{2} \qquad
-\text{(D)}\ \sqrt{3}\qquad
+\textbf{(D)}\ \sqrt{3}\qquad
-\text{(E)}\ </math>
+\textbf{(E)}\ 2</math>
 [[1983 AHSME Problems/Problem 4|Solution]]
@@ Line 57: / Line 62: @@
 \textbf{(B)}\ \frac{\sqrt 5}{3}\qquad
 \textbf{(C)}\ \frac{2}{\sqrt 5}\qquad
-\text{(D)}\ \sqrt{3}\qquad
+\textbf{(D)}\ \frac{\sqrt{5}}{2}\qquad
-\text{(E)}\ 2</math>
+\textbf{(E)}\ \frac{5}{3}</math>
 [[1983 AHSME Problems/Problem 5|Solution]]
@@ Line 64: / Line 69: @@
 == Problem 6 ==
-When <math>x^5, x+\frac{1}{x}</math> and <math>1+\frac{2}{x} + \frac{3}{x^2}</math> are multiplied, the product is a polynomial of degree.
+When <math>x^5, x+\frac{1}{x}</math> and <math>1+\frac{2}{x} + \frac{3}{x^2}</math> are multiplied, the product is a polynomial of degree
 <math>\textbf{(A)}\ 2\qquad
@@ Line 76: / Line 81: @@
 == Problem 7 ==
-Alice sells an item at &#036; <math>10</math> less than the list price and receives <math>10\%</math> of her selling price as her commission.
+Alice sells an item at <math>\$10</math> less than the list price and receives <math>10\%</math> of her selling price as her commission.
-Bob sells the same item at &#036; <math>20</math> less than the list price and receives <math>20\%</math> of his selling price as his commission.
+Bob sells the same item at <math>\$20</math> less than the list price and receives <math>20\%</math> of his selling price as his commission.
-If they both get the same commission, then the list price in dollars is
+If they both get the same commission, then the list price is
-<math>\textbf{(A) } 20\qquad
-\textbf{(B) } 30\qquad
-\textbf{(C) } 50\qquad
-\textbf{(D) } 70\qquad
-\textbf{(E) } 100 </math>
+<math>\textbf{(A) } \$20\qquad
+\textbf{(B) } \$30\qquad
+\textbf{(C) } \$50\qquad
+\textbf{(D) } \$70\qquad
+\textbf{(E) } \$100 </math>
 [[1983 AHSME Problems/Problem 7|Solution]]
@@ Line 118: / Line 122: @@
 Segment <math>AB</math> is both a diameter of a circle of radius <math>1</math> and a side of an equilateral triangle <math>ABC</math>.
-The circle also intersects <math>AC</math> and <math>BD</math> at points <math>D</math> and <math>E</math>, respectively. The length of <math>AE</math> is
+The circle also intersects <math>AC</math> and <math>BC</math> at points <math>D</math> and <math>E</math>, respectively. The length of <math>AE</math> is
 <math>
-\text{(A)} \ \frac{3}{2} \qquad
+\textbf{(A)} \ \frac{3}{2} \qquad
-\text{(B)} \ \frac{5}{3} \qquad
+\textbf{(B)} \ \frac{5}{3} \qquad
-\text{(C)} \ \frac{\sqrt 3}{2} \qquad
+\textbf{(C)} \ \frac{\sqrt 3}{2} \qquad
-\text{(D)}\ \sqrt{3}\qquad
+\textbf{(D)}\ \sqrt{3}\qquad
-\text{(E)}\ \frac{2+\sqrt 3}{2} </math>
+\textbf{(E)}\ \frac{2+\sqrt 3}{2} </math>
 [[1983 AHSME Problems/Problem 10|Solution]]
@@ Line 143: / Line 147: @@
 == Problem 12 ==
-If <math>\log_2 \Big(\log_3 (\log_2 x) \Big) = 0</math>, then <math>x^{-1/2}</math> equals
+If <math>\log_7 \Big(\log_3 (\log_2 x) \Big) = 0</math>, then <math>x^{-1/2}</math> equals
 <math>
-\text{(A)} \ \frac{1}{3} \qquad
+\textbf{(A)} \ \frac{1}{3} \qquad
-\text{(B)} \ \frac{1}{2 \sqrt 3} \qquad
+\textbf{(B)} \ \frac{1}{2 \sqrt 3} \qquad
-\text{(C)}\ \frac{1}{3\sqrt 3}\qquad
+\textbf{(C)}\ \frac{1}{3\sqrt 3}\qquad
-\text{(D)}\ \frac{1}{\sqrt{42}}\qquad
+\textbf{(D)}\ \frac{1}{\sqrt{42}}\qquad
-\text{(E)}\ \text{none of these} </math>
+\textbf{(E)}\ \text{none of these} </math>
 [[1983 AHSME Problems/Problem 12|Solution]]
@@ Line 156: / Line 160: @@
 == Problem 13 ==
-If <math>xy = a, xz =b,</math> and <math>yz = c</math>, and none of these quantities is zero, then <math>x^2+y^2+z^2</math> equals:
+If <math>xy = a, xz =b,</math> and <math>yz = c</math>, and none of these quantities is <math>0</math>, then <math>x^2+y^2+z^2</math> equals
 <math>\textbf{(A)}\ \frac{ab+ac+bc}{abc}\qquad
@@ Line 168: / Line 172: @@
 == Problem 14 ==
-The units digit of <math>3^{1001}* 7^{1002}* 13^{1003}</math> is
+The units digit of <math>3^{1001} 7^{1002} 13^{1003}</math> is
 <math>\textbf{(A)}\ 1\qquad
@@ Line 180: / Line 184: @@
 == Problem 15 ==
-Three balls marked <math>1,2</math>, and <math>3</math>, are placed in an urn. One ball is drawn, its number is recorded,
+Three balls marked <math>1,2</math> and <math>3</math> are placed in an urn. One ball is drawn, its number is recorded, and then the ball is returned to the urn. This process is repeated and then repeated once more, and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is <math>6</math>, what is the probability that the ball numbered <math>2</math> was drawn all three times?
-then the ball is returned to the urn. This process is repeated and then repeated once more,
-and each ball is equally likely to be drawn on each occasion. If the sum of the numbers recorded is <math>6</math>,
-what is the probability that the ball numbered <math>2</math> was drawn all three times?
 <math>
-\text{(A)} \ \frac{1}{27} \qquad
+\textbf{(A)} \ \frac{1}{27} \qquad
-\text{(B)} \ \frac{1}{8} \qquad
+\textbf{(B)} \ \frac{1}{8} \qquad
-\text{(C)} \ \frac{1}{7} \qquad
+\textbf{(C)} \ \frac{1}{7} \qquad
-\text{(D)}\ \frac{1}{6}\qquad
+\textbf{(D)} \ \frac{1}{6} \qquad
-\text{(E)}\ \frac{1}{3} </math>
+\textbf{(E)}\ \frac{1}{3} </math>
 [[1983 AHSME Problems/Problem 15|Solution]]
@@ Line 197: / Line 198: @@
 Let <math>x = .123456789101112....998999</math>, where the digits are obtained by writing the integers <math>1</math> through <math>999</math> in order.
-The <math>1983</math>rd digit to the right of the decimal point is
+The <math>1983</math><sup>rd</sup> digit to the right of the decimal point is
 <math>\textbf{(A)}\ 2\qquad
@@ Line 209: / Line 210: @@
 == Problem 17 ==
-The diagram to the right shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
+[[File:pdfresizer.com-pdf-convert-q17.png]]
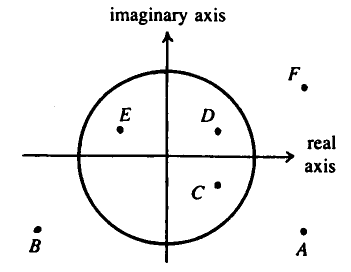
+The diagram above shows several numbers in the complex plane. The circle is the unit circle centered at the origin.
 One of these numbers is the reciprocal of <math>F</math>. Which one?
-<math>\text{(A)} \ A \qquad
+<math>\textbf{(A)} \ A \qquad
-\text{(B)} \ B \qquad
+\textbf{(B)} \ B \qquad
-\text{(C)} \ C \qquad
+\textbf{(C)} \ C \qquad
-\text{(D)} \ D \qquad
+\textbf{(D)} \ D \qquad
-\text{(E)} \ E  </math>
+\textbf{(E)} \ E  </math>
 [[1983 AHSME Problems/Problem 17|Solution]]
@@ Line 229: / Line 232: @@
 \textbf{(B)}\ x^4+x^2-3\qquad
 \textbf{(C)}\ x^4-5x^2+1\qquad
-\textbf{(D)}\ x^4+x^2+3\qquad\\
+\textbf{(D)}\ x^4+x^2+3\qquad
-\textbf{(E)}\ \text{None of these}  </math>
+\textbf{(E)}\ \text{none of these}  </math>
 [[1983 AHSME Problems/Problem 18|Solution]]
@@ Line 240: / Line 243: @@
 then the length of <math>AD</math> is
-<math>\text{(A)} \ 2 \qquad
+<math>\textbf{(A)} \ 2 \qquad
-\text{(B)} \ 2.5 \qquad
+\textbf{(B)} \ 2.5 \qquad
-\text{(C)} \ 3 \qquad
+\textbf{(C)} \ 3 \qquad
-\text{(D)} \ 3.5 \qquad
+\textbf{(D)} \ 3.5 \qquad
-\text{(E)} \ 4  </math>
+\textbf{(E)} \ 4  </math>
 [[1983 AHSME Problems/Problem 19|Solution]]
@@ Line 253: / Line 256: @@
 are the roots of <math>x^2 - rx + s = 0</math>, then <math>rs</math> is necessarily
-<math>\text{(A)} \ pq \qquad
+<math>\textbf{(A)} \ pq \qquad
-\text{(B)} \ \frac{1}{pq} \qquad
+\textbf{(B)} \ \frac{1}{pq} \qquad
-\text{(C)} \ \frac{p}{q^2} \qquad
+\textbf{(C)} \ \frac{p}{q^2} \qquad
-\text{(D)}\ \frac{q}{p^2}\qquad
+\textbf{(D)}\ \frac{q}{p^2}\qquad
-\text{(E)}\ \frac{p}{q}</math>
+\textbf{(E)}\ \frac{p}{q}</math>
 [[1983 AHSME Problems/Problem 20|Solution]]
@@ Line 263: / Line 266: @@
 == Problem 21 ==
-Find the smallest positive number from the numbers below
+Find the smallest positive number from the numbers below.
-<math>\text{(A)} \ 10-3\sqrt{11} \qquad
+<math>\textbf{(A)} \ 10-3\sqrt{11} \qquad
-\text{(B)} \ 3\sqrt{11}-10 \qquad
+\textbf{(B)} \ 3\sqrt{11}-10 \qquad
-\text{(C)}\ 18-5\sqrt{13}\qquad\\
+\textbf{(C)}\ 18-5\sqrt{13}\qquad
-\text{(D)}\ 51-10\sqrt{26}\qquad
+\textbf{(D)}\ 51-10\sqrt{26}\qquad
-\text{(E)}\ 10\sqrt{26}-51 </math>
+\textbf{(E)}\ 10\sqrt{26}-51 </math>
 [[1983 AHSME Problems/Problem 21|Solution]]
@@ Line 276: / Line 279: @@
 Consider the two functions <math>f(x) = x^2+2bx+1</math> and <math>g(x) = 2a(x+b)</math>, where the variable <math>x</math> and the constants <math>a</math> and <math>b</math> are real numbers.
-Each such pair of the constants a and b may be considered as a point <math>(a,b)</math> in an <math>ab</math>-plane.
+Each such pair of constants <math>a</math> and <math>b</math> may be considered as a point <math>(a,b)</math> in an <math>ab</math>-plane.
-Let S be the set of such points <math>(a,b)</math> for which the graphs of <math>y = f(x)</math> and <math>y = g(x)</math> do NOT intersect (in the <math>xy</math>- plane.). The area of <math>S</math> is
+Let <math>S</math> be the set of such points <math>(a,b)</math> for which the graphs of <math>y = f(x)</math> and <math>y = g(x)</math> do '''not''' intersect (in the <math>xy</math>-plane). The area of <math>S</math> is
-<math>\text{(A)} \ 1 \qquad
+<math>\textbf{(A)} \ 1 \qquad
-\text{(B)} \ \pi \qquad
+\textbf{(B)} \ \pi \qquad
-\text{(C)} \ 4 \qquad
+\textbf{(C)} \ 4 \qquad
-\text{(D)} \ 4 \pi \qquad
+\textbf{(D)} \ 4 \pi \qquad
-\text{(E)} \ \infty     </math>
+\textbf{(E)} \ \text{infinite}     </math>
 [[1983 AHSME Problems/Problem 22|Solution]]
@@ Line 290: / Line 293: @@
 In the adjoining figure the five circles are tangent to one another consecutively and to the lines
-<math>L_1</math> and <math>L_2</math> (<math>L_1</math> is the line that is above the circles and <math>L_2</math> is the line that goes under the circles).
+<math>L_1</math> and <math>L_2</math>.
 If the radius of the largest circle is <math>18</math> and that of the smallest one is <math>8</math>, then the radius of the middle circle is
@@ Line 313: / Line 316: @@
 label("$L_1$", Z1, dir(2*alpha)*dir(90));</asy>
-<math>\text{(A)} \ 12 \qquad
+<math>\textbf{(A)} \ 12 \qquad
-\text{(B)} \ 12.5 \qquad
+\textbf{(B)} \ 12.5 \qquad
-\text{(C)} \ 13 \qquad
+\textbf{(C)} \ 13 \qquad
-\text{(D)} \ 13.5 \qquad
+\textbf{(D)} \ 13.5 \qquad
-\text{(E)} \ 14    </math>
+\textbf{(E)} \ 14    </math>
-[[1983 AHSME Problems/Problem 22|Solution]]
+[[1983 AHSME Problems/Problem 23|Solution]]
 == Problem 24 ==
@@ Line 325: / Line 328: @@
 How many non-congruent right triangles are there such that the perimeter in <math>\text{cm}</math> and the area in <math>\text{cm}^2</math> are numerically equal?
-<math>\text{(A)} \ \text{none} \qquad
+<math>\textbf{(A)} \ \text{none} \qquad
-\text{(B)} \ 1 \qquad
+\textbf{(B)} \ 1 \qquad
-\text{(C)} \ 2 \qquad
+\textbf{(C)} \ 2 \qquad
-\text{(D)} \ 4 \qquad
+\textbf{(D)} \ 4 \qquad
-\text{(E)} \ \infty</math>
+\textbf{(E)} \ \text{infinitely many}</math>
 [[1983 AHSME Problems/Problem 24|Solution]]
@@ Line 335: / Line 338: @@
 == Problem 25 ==
-If <math>60^a = 3</math> and <math>60^b = 5</math>, then <math>12^{[(1-a-b)/2(1-b)]} </math>
+If <math>60^a = 3</math> and <math>60^b = 5</math>, then <math>12^{(1-a-b)/\left(2\left(1-b\right)\right)}</math> is
-<math>\text{(A)} \ \sqrt{3} \qquad
+<math>\textbf{(A)} \ \sqrt{3} \qquad
-\text{(B)} \ 2 \qquad
+\textbf{(B)} \ 2 \qquad
-\text{(C)} \ \sqrt{5} \qquad
+\textbf{(C)} \ \sqrt{5} \qquad
-\text{(D)} \ 3 \qquad
+\textbf{(D)} \ 3 \qquad
-\text{(E)} \ \sqrt{12} </math>
+\textbf{(E)} \ \sqrt{12} </math>
 [[1983 AHSME Problems/Problem 25|Solution]]
@@ Line 421: / Line 424: @@
 <asy>
-defaultpen(linewidth(0.7)+fontsize(10));
+import geometry;
-pair C=origin, N=dir(0), B=dir(20), A=dir(135), M=dir(180), P=(3/7)*dir(C--N);
+import graph;
-draw(M--N^^C--A--P--B--C^^Arc(origin,1,0,180));
-markscalefactor=0.03;
+unitsize(2 cm);
-draw(anglemark(C,A,P));
-draw(anglemark(C,B,P));
+pair A, B, C, M, N, P;
-pair point=C;
-label("$A$", A, dir(point--A));
+M = (-1,0);
-label("$B$", B, dir(point--B));
+N = (1,0);
+C = (0,0);
+A = dir(140);
+B = dir(20);
+P = extension(A, A + rotate(10)*(C - A), B, B + rotate(10)*(C - B));
+draw(M--N);
+draw(arc(C,1,0,180));
+draw(A--C--B);
+draw(A--P--B);
+label("$A$", A, NW);
+label("$B$", B, E);
 label("$C$", C, S);
-label("$M$", M, dir(point--M));
+label("$M$", M, SW);
-label("$N$", N, dir(point--N));
+label("$N$", N, SE);
 label("$P$", P, S);
-label("$40^\circ$", C, NW);
+</asy>
-label("$10^\circ$", B, SE);
-label("$10^\circ$", A+(0.05,0.02), SW);</asy>
 <math>\textbf{(A)}\ 10^{\circ}\qquad
@@ Line 443: / Line 456: @@
 \textbf{(D)}\ 25^{\circ}\qquad
 \textbf{(E)}\ 30^{\circ} </math>
+[[1983 AHSME Problems/Problem 30|Solution]]
 == See also ==