Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1961 AHSME Problems/Problem 11"

(→‎Solution)
m (→‎Solution 2 (Non-rigorous))
 
(One intermediate revision by the same user not shown)
Line 21: Line 21:
 
<cmath>AB + AC</cmath>
 
<cmath>AB + AC</cmath>
 
Thus, the perimeter of the triangle is <math>40</math>, so the answer is <math>\boxed{\textbf{(C)}}</math>.
 
Thus, the perimeter of the triangle is <math>40</math>, so the answer is <math>\boxed{\textbf{(C)}}</math>.
 +
 +
==Solution 2 (Non-rigorous)==
 +
 +
Since <math>Q</math> can be anywhere on the circle between <math>A</math> and <math>B</math>, it can basically be "on top" of <math>A</math>. Then <math>R</math> will be at the same point as <math>A</math>, so <math>APR</math> form a degenerate triable with side length <math>AB=20</math>. So its perimeter will be <math>40</math>. Since <math>BP=PQ</math> and <math>QR=CR</math> by power of a point, as <math>AP</math> and <math>AR</math> decrease in length, <math>PR=PQ+QR</math> will "grow" to compensate, so the perimeter will stay constant with a value of <math>\boxed{\textbf{(C)}\ 40}</math>.
 +
 +
We can also skip verifying that the perimeter will stay constant, since it seems unlikely that MAA would create a question with <math>\text{not determined by the given information}</math> as the answer.
 +
 +
~jd9
  
 
==See Also==
 
==See Also==

Latest revision as of 12:10, 16 November 2022

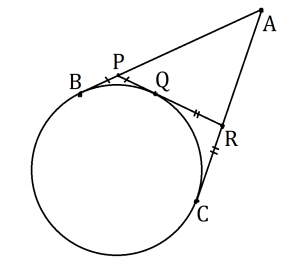
Problem

Two tangents are drawn to a circle from an exterior point $A$; they touch the circle at points $B$ and $C$ respectively. A third tangent intersects segment $AB$ in $P$ and $AC$ in $R$, and touches the circle at $Q$. If $AB=20$, then the perimeter of $\triangle APR$ is

$\textbf{(A)}\ 42\qquad \textbf{(B)}\ 40.5 \qquad \textbf{(C)}\ 40\qquad \textbf{(D)}\ 39\frac{7}{8} \qquad \textbf{(E)}\ \text{not determined by the given information}$

Solution

1961 AHSME Problem 11.png

Draw the diagram as shown. Note that the two tangent lines from a single outside point of a circle have the exact same length, so $AB = AC = 20$, $BP = PQ$, and $QR = CR$.

The perimeter of the triangle is $AP + PR + AR$. Note that $PQ + QR = PR$, so from substitution, the perimeter is \[AP + PQ + QR + AR\] \[AP + BP + CR + AR\] \[AB + AC\] Thus, the perimeter of the triangle is $40$, so the answer is $\boxed{\textbf{(C)}}$.

Solution 2 (Non-rigorous)

Since $Q$ can be anywhere on the circle between $A$ and $B$, it can basically be "on top" of $A$. Then $R$ will be at the same point as $A$, so $APR$ form a degenerate triable with side length $AB=20$. So its perimeter will be $40$. Since $BP=PQ$ and $QR=CR$ by power of a point, as $AP$ and $AR$ decrease in length, $PR=PQ+QR$ will "grow" to compensate, so the perimeter will stay constant with a value of $\boxed{\textbf{(C)}\ 40}$.

We can also skip verifying that the perimeter will stay constant, since it seems unlikely that MAA would create a question with $\text{not determined by the given information}$ as the answer.

~jd9

See Also

1961 AHSC (Problems • Answer Key • Resources)
Preceded by
Problem 10 		Followed by
Problem 12
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25 • 26 • 27 • 28 • 29 • 30 • 31 • 32 • 33 • 34 • 35 • 36 • 37 • 38 • 39 • 40
All AHSME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1961_AHSME_Problems/Problem_11&oldid=181679"