Difference between revisions of "2018 AMC 10B Problems/Problem 10"

Latest revision as of 12:29, 21 April 2024

Problem

In the rectangular parallelepiped shown, $AB$ = $3$ , $BC$ = $1$ , and $CG$ = $2$ . Point $M$ is the midpoint of $\overline{FG}$ . What is the volume of the rectangular pyramid with base $BCHE$ and apex $M$ ?

$[asy] size(250); defaultpen(fontsize(10pt)); pair A =origin; pair B = (4.75,0); pair E1=(0,3); pair F = (4.75,3); pair G = (5.95,4.2); pair C = (5.95,1.2); pair D = (1.2,1.2); pair H= (1.2,4.2); pair M = ((4.75+5.95)/2,3.6); draw(E1--M--H--E1--A--B--E1--F--B--M--C--G--H); draw(B--C); draw(F--G); draw(A--D--H--C--D,dashed); label("$A$",A,SW); label("$B$",B,SE); label("$C$",C,E); label("$D$",D,W); label("$E$",E1,W); label("$F$",F,SW); label("$G$",G,NE); label("$H$",H,NW); label("$M$",M,N); dot(A); dot(B); dot(E1); dot(F); dot(G); dot(C); dot(D); dot(H); dot(M); label("3",A/2+B/2,S); label("2",C/2+G/2,E); label("1",C/2+B/2,SE); [/asy]$

$\textbf{(A) } 1 \qquad \textbf{(B) } \frac{4}{3} \qquad \textbf{(C) } \frac{3}{2} \qquad \textbf{(D) } \frac{5}{3} \qquad \textbf{(E) } 2$

Solution 1

Consider the cross-sectional plane and label its area $b$ . Note that the volume of the triangular prism that encloses the pyramid is $\frac{bh}{2}=3$ , and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is $\frac{bh}{3}$ , so the answer is $\boxed{(E) 2}$ .(AOPS12142015)

Solution 2

We can start by finding the total volume of the parallelepiped. It is $2 \cdot 3 \cdot 1 = 6$ , because a rectangular parallelepiped is a rectangular prism.

Next, we can consider the wedge-shaped section made when the plane $BCHE$ cuts the figure. We can find the volume of the triangular pyramid with base $EFB$ and apex $M$ . The area of $EFB$ is $\frac{1}{2} \cdot 2 \cdot 3 = 3$ . Since $\overline{BC}$ is given to be $1$ , we have that $\overline{FM}$ is $\frac{1}{2}$ . Using the formula for the volume of a triangular pyramid, we have $V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2}$ . Also, since the triangular pyramid with base $HGC$ and apex $M$ has the exact same dimensions, it has volume $\frac{1}{2}$ as well.

The original wedge we considered in the last step has volume $3$ , because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have $3 - \frac{1}{2} \cdot 2 = 2$ . Thus, the volume of the figure we are trying to find is $2$ . This means that the correct answer choice is $\boxed{E}$ .

Written by: Archimedes15

NOTE: For those who think that it isn't a rectangular prism, please read the problem. It says "rectangular parallelepiped." If a parallelepiped is such that all of the faces are rectangles, it is a rectangular prism.

Solution 3

If you look carefully, you will see that on the either side of the pyramid in question, there are two congruent tetrahedra. The volume of one is $\frac{1}{3}Bh$ , with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is $\frac{1}{3} (3 \times 2/2 \times \frac{1}{2})=\frac{1}{2}$ . We can obtain the answer by subtracting twice this value from the diagonal half prism, or $(\frac{1}{2} \times 3 \times 2 \times 1) - (2 \times \frac{1}{2})=$ $\boxed{2}$

Solution 4

You can calculate the volume of the rectangular pyramid by using the formula, $\frac{Ah}{3}$ . $A$ is the area of the base, $BCHE$ , and is equal to $BC * BE$ . The height, $h$ , is equal to the height of triangle $FBE$ drawn from $F$ to $BE$ .

$BE=\sqrt{BF^2 + EF^2}=\sqrt{13}$ Area of $BCHE = BC * BE = \sqrt{13}$

$h = 2 *$ Area of $FBE / BE$ (since Area $= \frac{1}{2}bh$ ).

Area of $FBE = \frac{1}{2} * FB * FE = 3$

$h = 2 * 3 / \sqrt{13} = \frac{6}{\sqrt{13}}$

Volume of pyramid $=\frac{1}{3} * \sqrt{13} * \frac{6}{\sqrt{13}} = 2$

Answer is $\boxed{\textbf{E } 2}$

~OlutosinNGA

Solution 5

We can start by identifying the information we need. We need to find the area of rectangle $EHCB$ and the height of rectangular prism $EHCBM$ .

In order to find the area of $EHCB,$ we can use the Pythagorean Theorem. We find that $EB = \sqrt{13}$ , so the area of rectangle $EHCB = \sqrt{13}$ . We shall refer to this as $x$ .

In order to find the height of rectangular prism $EHCBM$ , we can examine triangle $EFB$ . We can use the Geometric Mean Theorem to find that when an altitude is dropped from point $F,$ $\overline{EB}$ is split into segments of length $\dfrac{4 \cdot \sqrt{13}}{13}$ and $\dfrac{9 \cdot \sqrt{13}}{13}$ . Taking the geometric mean of these numbers, we find that the altitude has length $\dfrac{6 \cdot \sqrt{13}}{13}$ . This is also the height of the rectangular prism, which we shall refer to as $y$ .

Plugging $x$ and $y$ into the formula $V = \dfrac{b \cdot h}{3},$ we find that the volume is $\boxed{2}$ . The answer is $\boxed{E}$ .

Solution 6

We start by setting the formula for the volume of a rectangular pyramid: $\frac{1}{3}Bh$ . By the Pythagorean Theorem, we know that $BE = \sqrt{BF^2 + EF^2} = \sqrt{13}$ . Therefore, the area of the base is $1 \times \sqrt{13} = \sqrt{13}$ . Next, we would like to know the height of the pyramid. We can observe that the altitude from point $F$ in $\triangle EFB$ is parallel to the height of the pyramid and therefore congruent because those two altitudes are on the same plane of base $EBCH$ . From this, we only need to find the altitude from point $F$ in $\triangle EFB$ and plug it into our formula for the volume of a rectangular pyramid. This is easy because we already know the area of $\triangle EFB$ and the base from point $F$ , so all we need to do is divide: $\frac{2 \times 3}{\sqrt{13}} = \frac{6}{\sqrt{13}} = \frac{6\sqrt{13}}{13}$ . Now all we need to do is plug in all our known values into the volume formula: $\frac{1}{3}Bh = \frac{\sqrt{13} \times \frac{6\sqrt{13}}{13}}{3} = \boxed{(E) 2}$

~ellpet

Solution 7

Using the Pythagorean Theorem, we can easily find that $EB = \sqrt{2^2 + 3^2} = \sqrt{13}$ . Quickly computing, we find the area of the base, $BCHE = \sqrt{13} \cdot 1 = \sqrt{13}$ . Now we can make the following adjustments to our 3d shape as shown in the diagram. All we need now is to solve for the height, or $XM$ . We can set up to following equation due to our knowledge of altitudes(of the hypotenuse)in right triangles. We can set up the following equations: $\begin{align*} b(a+b) &= (MH_1)^2 \\ a(a+b) &= (MH_2)^2 \\ b\sqrt{13} &= 3^2 \\ a\sqrt{13} &= 2^2 \\ b &= \dfrac{9}{\sqrt{13}} \\ a &= \dfrac{4}{\sqrt{13}} \\ (MX)^2 &= ab \\ (MX)^2 &= \dfrac{9 \cdot 4}{13} \\ MX &= \dfrac {3 \cdot 2}{\sqrt{13}} \\ \end{align*}$ Thus $\triangle V_{BCHEM} = \dfrac{\text{(height)}\cdot \text{(base)}}{3} = \dfrac{MX \cdot BCHE}{3} = \dfrac {\sqrt{13} \cdot \dfrac{3 \cdot 2}{\sqrt{13}}}{3}$ $= \boxed{\textbf{(E) } 2}$

~ Wiselion :)

Video Solution (HOW TO THINK CREATIVELY)

https://youtu.be/tlbbP_NdPmc

~Education, the Study of Everything

@@ Line 1: / Line 1: @@
-In the rectangular parallelpiped shown, <math>AB</math> = <math>3</math>, <math>BC</math> = <math>1</math>, and <math>CG</math> = <math>2</math>. Point <math>M</math> is the midpoint of <math>\overline{FG}</math>. What is the volume of the rectangular pyramid with base <math>BCHE</math> and apex <math>M</math>?
+== Problem ==
+In the rectangular parallelepiped shown, <math>AB</math> = <math>3</math>, <math>BC</math> = <math>1</math>, and <math>CG</math> = <math>2</math>. Point <math>M</math> is the midpoint of <math>\overline{FG}</math>. What is the volume of the rectangular pyramid with base <math>BCHE</math> and apex <math>M</math>?
 <asy>
 size(250);
 defaultpen(fontsize(10pt));
@@ Line 36: / Line 37: @@
 dot(D);
 dot(H);
-dot(M);</asy>
+dot(M);
+label("3",A/2+B/2,S);
+label("2",C/2+G/2,E);
+label("1",C/2+B/2,SE);
+</asy>
 <math>\textbf{(A) } 1 \qquad \textbf{(B) } \frac{4}{3} \qquad \textbf{(C) } \frac{3}{2} \qquad \textbf{(D) } \frac{5}{3} \qquad \textbf{(E) } 2</math>
 ==Solution 1==
-Consider the cross-sectional plane. Note that <math>bh/2=3</math> and we want <math>bh/3</math>, so the answer is <math>\boxed{2}</math>. (AOPS12142015)
+Consider the cross-sectional plane and label its area <math>b</math>. Note that the volume of the triangular prism that encloses the pyramid is <math>\frac{bh}{2}=3</math>, and we want the rectangular pyramid that shares the base and height with the triangular prism. The volume of the pyramid is <math>\frac{bh}{3}</math>, so the answer is <math>\boxed{(E) 2}</math>.(AOPS12142015)
 ==Solution 2==
-We start by finding side <math>\overline{BE}</math> of base <math>BCHE</math> by using the Pythagorean theorem on <math>\triangle ABE</math>. Doing this, we get
+We can start by finding the total volume of the parallelepiped. It is <math>2 \cdot 3 \cdot 1 = 6</math>, because a rectangular parallelepiped is a rectangular prism.
+Next, we can consider the wedge-shaped section made when the plane <math>BCHE</math> cuts the figure. We can find the volume of the triangular pyramid with base <math>EFB</math> and apex <math>M</math>. The area of <math>EFB</math> is <math>\frac{1}{2} \cdot 2 \cdot 3 = 3</math>. Since <math>\overline{BC}</math> is given to be <math>1</math>, we have that <math>\overline{FM}</math> is <math>\frac{1}{2}</math>. Using the formula for the volume of a triangular pyramid, we have <math>V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2}</math>. Also, since the triangular pyramid with base <math>HGC</math> and apex <math>M</math> has the exact same dimensions, it has volume <math>\frac{1}{2}</math> as well.
+The original wedge we considered in the last step has volume <math>3</math>, because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have <math>3 - \frac{1}{2} \cdot 2 = 2</math>. Thus, the volume of the figure we are trying to find is <math>2</math>. This means that the correct answer choice is <math>\boxed{E}</math>.
+Written by: Archimedes15
+NOTE: For those who think that it isn't a rectangular prism, please read the problem. It says "rectangular parallelepiped." If a parallelepiped is such that all of the faces are rectangles, it is a rectangular prism.
-<cmath>\overline{BE}^2 = \overline{AB}^2  + \overline{AE}^2 = 3^2 + 2^2 = 13.</cmath>
+==Solution 3==
+If you look carefully, you will see that on the either side of the pyramid in question, there are two congruent tetrahedra. The volume of one is <math>\frac{1}{3}Bh</math>, with its base being half of one of the rectangular prism's faces and its height being half of one of the edges, so its volume is <math>\frac{1}{3} (3 \times 2/2 \times \frac{1}{2})=\frac{1}{2}</math>. We can obtain the answer by subtracting twice this value from the diagonal half prism, or
+<math>(\frac{1}{2} \times 3 \times 2 \times 1) - (2 \times \frac{1}{2})= </math> <math>\boxed{2}</math>
-Taking the square root of both sides of the equation, we get <math>\overline{BE} = \sqrt {13}</math>. We can then find the area of rectangle <math>BCHE</math>, noting that
+==Solution 4==
+You can calculate the volume of the rectangular pyramid by using the formula, <math>\frac{Ah}{3}</math>. <math>A</math> is the area of the base, <math>BCHE</math>, and is equal to <math>BC * BE</math>. The height, <math>h</math>, is equal to the height of triangle <math>FBE</math> drawn from <math>F</math> to <math>BE</math>.
-<cmath>[BCHE] = \overline{BE} \cdot \overline{BC} = \sqrt {13} \cdot 1 = \sqrt {13}.</cmath>
+<math>BE=\sqrt{BF^2 + EF^2}=\sqrt{13}</math> Area of <math>BCHE = BC * BE = \sqrt{13}</math>
+<math>h = 2 *</math> Area of <math>FBE / BE</math> (since Area <math>= \frac{1}{2}bh</math>).
-Taking the vertical cross-sectional plane of the rectangular prism, we see that the distance from point <math>M</math> to base <math>BCHE</math> is the same as the distance from point <math>F</math> to side <math>\overline{BE}</math>. Calling the point where the altitude from vertex <math>F</math> touches side <math>\overline{BE}</math> as point <math>K</math>, we can easily find this altitude using the area of right <math>\triangle BFE</math>, as
+Area of <math>FBE = \frac{1}{2} * FB * FE = 3</math>
-<cmath>\frac{\overline{BF} \cdot \overline{FE}}{2} = \frac{\overline{BE} \cdot FK}{2}.</cmath>
+<math>h = 2 * 3 / \sqrt{13} = \frac{6}{\sqrt{13}}</math>
-Multiplying both sides of the equation by 2 and substituting in known values, we get
+Volume of pyramid <math>=\frac{1}{3} * \sqrt{13} * \frac{6}{\sqrt{13}} = 2</math>
-<cmath>2 \cdot 3 = FK \cdot \sqrt {13} \Rightarrow FK = \frac{6\sqrt {13}}{13}.</cmath>
+Answer is <math>\boxed{\textbf{E } 2}</math>
-Deducing that the altitude from vertex <math>M</math> to base <math>BCHE</math> is <math>\frac{6\sqrt {13}}{13}</math> and calling the point of intersection between the altitude and the base as point <math>N</math>, we get the area of the rectangular pyramid to be
+~OlutosinNGA
-<cmath>\frac{1}{3}([BCHE] \cdot MN) = \frac{1}{3}\left(\sqrt {13} \cdot \frac{6\sqrt {13}}{13}\right) = \frac{6}{3} = \boxed{2}.</cmath>
+== Solution 5 ==
+We can start by identifying the information we need. We need to find the area of rectangle <math>EHCB</math> and the height of rectangular prism <math>EHCBM</math>.
-Written by: Adharshk
+In order to find the area of <math>EHCB,</math> we can use the Pythagorean Theorem. We find that <math>EB = \sqrt{13}</math>, so the area of rectangle <math>EHCB = \sqrt{13}</math>. We shall refer to this as <math>x</math>.
-==Solution 3==
+In order to find the height of rectangular prism <math>EHCBM</math>, we can examine triangle <math>EFB</math>. We can use the Geometric Mean Theorem to find that when an altitude is dropped from point <math>F,</math>  <math>\overline{EB}</math> is split into segments of length <math>\dfrac{4 \cdot \sqrt{13}}{13}</math> and <math>\dfrac{9 \cdot \sqrt{13}}{13}</math>. Taking the geometric mean of these numbers, we find that the altitude has length <math>\dfrac{6 \cdot \sqrt{13}}{13}</math>. This is also the height of the rectangular prism, which we shall refer to as <math>y</math>.
-We can start by finding the total volume of the parallelepiped. It is <math>2 \cdot 3 \cdot 1 = 6</math>, because a rectangular parallelepiped is a rectangular prism.
-Next, we can consider the wedge-shaped section made when the plane <math>BCHE</math> cuts the figure. We can find the volume of the triangular pyramid with base EFB and apex M. The area of EFB is <math>\frac{1}{2} \cdot 2 \cdot 3 = 3</math>. Since BC is given to be <math>1</math>, we have that FM is <math>\frac{1}{2}</math>. Using the formula for the volume of a triangular pyramid, we have <math>V = \frac{1}{3} \cdot \frac{1}{2} \cdot 3 = \frac{1}{2}</math>. Also, since the triangular pyramid with base HGC and apex M has the exact same dimensions, it has volume <math>\frac{1}{2}</math> as well.
+Plugging <math>x</math> and <math>y</math> into the formula <math>V = \dfrac{b \cdot h}{3},</math> we find that the volume is <math>\boxed{2}</math>. The answer is <math>\boxed{E}</math>.
-The original wedge we considered in the last step has volume <math>3</math>, because it is half of the volume of the parallelepiped. We can subtract out the parts we found to have <math>3 - \frac{1}{2} \cdot 2 = 2</math>. Thus, the volume of the figure we are trying to find is <math>2</math>. This means that the correct answer choice is <math>\boxed{E}</math>.
+== Solution 6 ==
+We start by setting the formula for the volume of a rectangular pyramid: <math>\frac{1}{3}Bh</math>. By the Pythagorean Theorem, we know that <math>BE = \sqrt{BF^2 + EF^2} = \sqrt{13}</math>. Therefore, the area of the base is <math>1 \times \sqrt{13} = \sqrt{13}</math>. Next, we would like to know the height of the pyramid. We can observe that the altitude from point <math>F</math> in <math>\triangle EFB</math> is parallel to the height of the pyramid and therefore congruent because those two altitudes are on the same plane of base <math>EBCH</math>. From this, we only need to find the altitude from point <math>F</math> in <math>\triangle EFB</math> and plug it into our formula for the volume of a rectangular pyramid. This is easy because we already know the area of <math>\triangle EFB</math> and the base from point <math>F</math>, so all we need to do is divide: <math>\frac{2 \times 3}{\sqrt{13}} = \frac{6}{\sqrt{13}} = \frac{6\sqrt{13}}{13}</math>. Now all we need to do is plug in all our known values into the volume formula: <math>\frac{1}{3}Bh = \frac{\sqrt{13} \times \frac{6\sqrt{13}}{13}}{3} = \boxed{(E) 2}</math>
-Written by: Archimedes15
+~ellpet
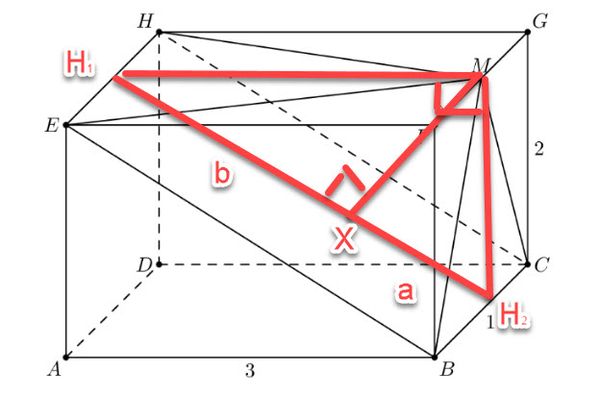
-==Solution 4 (Vectors)==
+== Solution 7 ==
-By the Pythagorean theorem, <math>EB=\sqrt{13}</math>. Because <math>EH=1</math>, the area of the base is <math>\sqrt{13}</math>. Now, we need to find the height.
-Define <math>X</math> as the midpoint of <math>BC</math> and <math>Y</math> as the midpoint of <math>EH</math>. Consider a vector coordinate system with origin <math>X</math> with <math>x, y,</math> and <math>z</math> axes parallel to <math>AB, BC,</math> and <math>CG</math> respectively (positive <math>x</math> direction is towards <math>A</math>, positive <math>y</math> direction is towards <math>C</math>, positive <math>z</math> direction is towards <math>G</math>). Then,
+[[File:AMC 10B 10 2018.jpg|600px]]
-<cmath>
-M=\begin{bmatrix}
-\\
-\\
-\\
-         \end{bmatrix},
-Y=\begin{bmatrix}
-\\
-\\
-\\
-         \end{bmatrix}
-</cmath>
-The dot product of <math>M</math> and <math>Y</math> is the length of the projection of <math>M</math> onto <math>Y</math> multiplied by the length of <math>Y</math>, so dividing the dot product of <math>M</math> and <math>Y</math> by the length of <math>Y</math> should give the length of the projection of <math>M</math> onto <math>Y</math>. Doing this calculation, we get that the length of the projection is <math>\frac4{\sqrt{13}}</math>. Notice that this projection onto <math>Y</math> is the same as projecting <math>M</math> onto the plane.
-Denote <math>P</math> as the foot of the projection of <math>M</math> onto <math>Y</math>. Then <math>\angle MPY</math> is right, so <math>\triangle MPY</math> is a right triangle. Applying the Pythagorean theorem on <math>\triangle MPY</math> and calling <math>MP</math> (which is actually the height of the pyramid) <math>x</math>, we get <math>x^2+\frac4{\sqrt{13}}^2=2^2</math>. Therefore, <math>x=\sqrt{4-\frac{16}{13}}=\frac6{\sqrt{13}}</math>.
+Using the Pythagorean Theorem, we can easily find that <math>EB = \sqrt{2^2 + 3^2} = \sqrt{13}</math>. Quickly computing, we find the area of the base, <math>BCHE = \sqrt{13} \cdot 1 = \sqrt{13}</math>. Now we can make the following adjustments to our 3d shape as shown in the diagram. All we need now is to solve for the height, or <math>XM</math>. We can set up to following equation due to our knowledge of altitudes(of the hypotenuse)in right triangles. We can set up the following equations:
+<cmath>\begin{align*}
+b(a+b) &= (MH_1)^2 \\
+a(a+b) &= (MH_2)^2 \\
+b\sqrt{13} &= 3^2 \\
+a\sqrt{13} &= 2^2 \\
+b &= \dfrac{9}{\sqrt{13}} \\
+a &= \dfrac{4}{\sqrt{13}} \\
+(MX)^2 &= ab \\
+(MX)^2 &= \dfrac{9 \cdot 4}{13} \\
+MX &= \dfrac {3 \cdot 2}{\sqrt{13}} \\
+\end{align*}</cmath>
+Thus <math>\triangle V_{BCHEM} = \dfrac{\text{(height)}\cdot \text{(base)}}{3} = \dfrac{MX \cdot BCHE}{3} = \dfrac {\sqrt{13} \cdot \dfrac{3 \cdot 2}{\sqrt{13}}}{3}</math> <math>= \boxed{\textbf{(E) } 2}</math>
-Now since we have the base and the height of the pyramid, we can find its volume. <math>\dfrac{\sqrt{13}\times\dfrac6{\sqrt{13}}}3=2</math>, so the answer is <math>\boxed{\text{(E)}}</math>.
+~ Wiselion :)
-Written by: SS4
+==Video Solution (HOW TO THINK CREATIVELY)==
-==Solution 5 (slicker method)==
+https://youtu.be/tlbbP_NdPmc
-Rotate the rectangular pyramid so that rectangle <math>GFBC</math> is the base of our rectangular pyramid. Now our height becomes <math>GH=3.</math> We know that the volume of our rectangular pyramid is <math>\dfrac{1}{3} \cdot [GFBC] \cdot GH= \dfrac{1}{3} \cdot 2 \cdot 3= \boxed{2}.</math>
-(MathloverMC)
+~Education, the Study of Everything
 ==See Also==
 {{AMC10 box|year=2018|ab=B|num-b=9|num-a=11}}
+[[Category:Introductory Geometry Problems]]
+[[Category:3D Geometry Problems]]
 {{MAA Notice}}

2018 AMC 10B (Problems • Answer Key • Resources)
Preceded by Problem 9	Followed by Problem 11
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15 • 16 • 17 • 18 • 19 • 20 • 21 • 22 • 23 • 24 • 25
All AMC 10 Problems and Solutions

Page

Toolbox

Search