Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2011 AIME II Problems/Problem 4"

m (format fixes)
(→‎Solution 1)
 
(20 intermediate revisions by 13 users not shown)
Line 1: Line 1:
 +
__TOC__
 +
 
== Problem 4 ==
 
== Problem 4 ==
−
In triangle <math>ABC</math>, <math>AB=\frac{20}{11} AC</math>. The angle bisector of <math>\angle A</math> intersects <math>BC</math> at point <math>D</math>, and point <math>M</math> is the midpoint of <math>AD</math>. Let <math>P</math> be the point of the intersection of <math>AC</math> and <math>BM</math>. The ratio of <math>CP</math> to <math>PA</math> can be expressed in the form <math>\dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
+
In triangle <math>ABC</math>, <math>AB=20</math> and <math>AC=11</math>. The angle bisector of <math>\angle A</math> intersects <math>BC</math> at point <math>D</math>, and point <math>M</math> is the midpoint of <math>AD</math>. Let <math>P</math> be the point of the intersection of <math>AC</math> and <math>BM</math>. The ratio of <math>CP</math> to <math>PA</math> can be expressed in the form <math>\dfrac{m}{n}</math>, where <math>m</math> and <math>n</math> are relatively prime positive integers. Find <math>m+n</math>.
−
 
 
−
__TOC__
 
  
−
== Solutions ==
+
== Solution 1 ==
−
=== Solution 1 ===
 
 
<asy>
 
<asy>
 
pointpen = black; pathpen = linewidth(0.7);
 
pointpen = black; pathpen = linewidth(0.7);
Line 13: Line 12:
 
D(MP("A",D(A))--MP("B",D(B),N)--MP("C",D(C))--cycle); D(A--MP("D",D(D),NE)--MP("D'",D(D2))); D(B--MP("P",D(P))); D(MP("M",M,NW)); MP("20",(B+D)/2,ENE); MP("11",(C+D)/2,ENE);
 
D(MP("A",D(A))--MP("B",D(B),N)--MP("C",D(C))--cycle); D(A--MP("D",D(D),NE)--MP("D'",D(D2))); D(B--MP("P",D(P))); D(MP("M",M,NW)); MP("20",(B+D)/2,ENE); MP("11",(C+D)/2,ENE);
  
−
</asy> Let <math>D'</math> be on <math>\overline{AC}</math> such that <math>BP \parallel DD'</math>. It follows that <math>\triangle BPC \sim \triangle DD'C</math>, so <cmath>\frac{PC}{D'C} = 1 + \frac{BD}{DC} = 1 + \frac{AB}{AC} = \frac{31}{11}</cmath> by the [[Angle Bisector Theorem]]. Similarly, we see by the midline theorem that <math>AP = PD'</math>. Thus, <cmath>\frac{CP}{PA} = \frac{1}{\frac{PD'}{PC}} = \frac{1}{1 - \frac{D'C}{PC}} = \frac{31}{20},</cmath> and <math>m+n = \boxed{051}</math>.
+
</asy> Let <math>D'</math> be on <math>\overline{AC}</math> such that <math>BP \parallel DD'</math>. It follows that <math>\triangle BPC \sim \triangle DD'C</math>, so <cmath>\frac{PC}{D'C} = 1 + \frac{BD}{DC} = 1 + \frac{AB}{AC} = \frac{31}{11}</cmath> by the [[Angle Bisector Theorem]]. Similarly, we see by the Midline Theorem that <math>AP = PD'</math>. Thus, <cmath>\frac{CP}{PA} = \frac{1}{\frac{PD'}{PC}} = \frac{1}{1 - \frac{D'C}{PC}} = \frac{31}{20},</cmath> and <math>m+n = \boxed{51}</math>.
  
−
=== Solution 2 ===
+
== Solution 2 (mass points) ==
−
Assign [[mass points]] as follows: by Angle-Bisector Theorem, <math>BD / DC = 20/11</math>, so we assign <math>m(B) = 11, m(C) = 20, m(D) = 31</math>. Since <math>AM = MD</math>, then <math>m(A) = 31</math>, and <math>\frac{CP}{PA} = \frac{m(A) }{ m(C)} = \frac{31}{20}</math>, so <math>m+n = \boxed{051}</math>.
+
Assign [[mass points]] as follows: by Angle-Bisector Theorem, <math>BD / DC = 20/11</math>, so we assign <math>m(B) = 11, m(C) = 20, m(D) = 31</math>. Since <math>AM = MD</math>, then <math>m(A) = 31</math>, and <math>\frac{CP}{PA} = \frac{m(A) }{ m(C)} = \frac{31}{20}</math>, so <math>m+n = \boxed{51}</math>.
  
−
=== Solution 3 ===
+
== Solution 3 ==
 
By [[Menelaus' Theorem]] on <math>\triangle ACD</math> with [[transversal]] <math>PB</math>, <cmath>1 = \frac{CP}{PA} \cdot \frac{AM}{MD} \cdot \frac{DB}{CB} = \frac{CP}{PA} \cdot \left(\frac{1}{1+\frac{AC}{AB}}\right) \quad \Longrightarrow \quad \frac{CP}{PA} = \frac{31}{20}. </cmath> So <math>m+n = \boxed{051}</math>.
 
By [[Menelaus' Theorem]] on <math>\triangle ACD</math> with [[transversal]] <math>PB</math>, <cmath>1 = \frac{CP}{PA} \cdot \frac{AM}{MD} \cdot \frac{DB}{CB} = \frac{CP}{PA} \cdot \left(\frac{1}{1+\frac{AC}{AB}}\right) \quad \Longrightarrow \quad \frac{CP}{PA} = \frac{31}{20}. </cmath> So <math>m+n = \boxed{051}</math>.
  
−
===Solution 4===
+
==Solution 4==
 
We will use barycentric coordinates. Let <math>A = (1, 0, 0)</math>, <math>B = (0, 1, 0)</math>, <math>C = (0, 0, 1)</math>. By the [[Angle Bisector Theorem]], <math>D = [0:11:20] = \left(0, \frac{11}{31}, \frac{20}{31}\right)</math>. Since <math>M</math> is the midpoint of <math>AD</math>, <math>M = \frac{A + D}{2} = \left(\frac{1}{2}, \frac{11}{62}, \frac{10}{31}\right)</math>. Therefore, the equation for line BM is <math>20x = 31z</math>. Let <math>P = (x, 0, 1-x)</math>. Using the equation for <math>BM</math>, we get <cmath>20x = 31(1-x)</cmath>
 
We will use barycentric coordinates. Let <math>A = (1, 0, 0)</math>, <math>B = (0, 1, 0)</math>, <math>C = (0, 0, 1)</math>. By the [[Angle Bisector Theorem]], <math>D = [0:11:20] = \left(0, \frac{11}{31}, \frac{20}{31}\right)</math>. Since <math>M</math> is the midpoint of <math>AD</math>, <math>M = \frac{A + D}{2} = \left(\frac{1}{2}, \frac{11}{62}, \frac{10}{31}\right)</math>. Therefore, the equation for line BM is <math>20x = 31z</math>. Let <math>P = (x, 0, 1-x)</math>. Using the equation for <math>BM</math>, we get <cmath>20x = 31(1-x)</cmath>
 
<cmath>x = \frac{31}{51}</cmath> Therefore, <math>\frac{CP}{PA} = \frac{1-x}{x} = \frac{31}{20}</math> so the answer is <math>\boxed{051}</math>.
 
<cmath>x = \frac{31}{51}</cmath> Therefore, <math>\frac{CP}{PA} = \frac{1-x}{x} = \frac{31}{20}</math> so the answer is <math>\boxed{051}</math>.
  
−
=== Solution 5 ===
+
== Solution 5 ==
 
Let <math>DC=x</math>. Then by the Angle Bisector Theorem, <math>BD=\frac{20}{11}x</math>. By the Ratio Lemma, we have that <math>\frac{PC}{AP}=\frac{\frac{31}{11}x\sin\angle PBC}{20\sin\angle ABP}.</math> Notice that <math>[\triangle BAM]=[\triangle BMD]</math> since their bases have the same length and they share a height. By the sin area formula, we have that <cmath>\frac{1}{2}\cdot20\cdot BM\cdot \sin\angle ABP=\frac{1}{2}\cdot \frac{20}{11}x\cdot BM\cdot\sin\angle PBC.</cmath> Simplifying, we get that <math>\frac{\sin\angle PBC}{\sin\angle ABP}=\frac{11}{x}.</math> Plugging this into what we got from the Ratio Lemma, we have that <math>\frac{PC}{AP}=\frac{31}{20}\implies\boxed{051.}</math>
 
Let <math>DC=x</math>. Then by the Angle Bisector Theorem, <math>BD=\frac{20}{11}x</math>. By the Ratio Lemma, we have that <math>\frac{PC}{AP}=\frac{\frac{31}{11}x\sin\angle PBC}{20\sin\angle ABP}.</math> Notice that <math>[\triangle BAM]=[\triangle BMD]</math> since their bases have the same length and they share a height. By the sin area formula, we have that <cmath>\frac{1}{2}\cdot20\cdot BM\cdot \sin\angle ABP=\frac{1}{2}\cdot \frac{20}{11}x\cdot BM\cdot\sin\angle PBC.</cmath> Simplifying, we get that <math>\frac{\sin\angle PBC}{\sin\angle ABP}=\frac{11}{x}.</math> Plugging this into what we got from the Ratio Lemma, we have that <math>\frac{PC}{AP}=\frac{31}{20}\implies\boxed{051.}</math>
 +
 +
== Solution 6 (quick Menelaus) ==
 +
First, we will find <math>\frac{MP}{BP}</math>. By Menelaus on <math>\triangle BDM</math> and the line <math>AC</math>, we have
 +
<cmath>\frac{BC}{CD}\cdot\frac{DA}{AM}\cdot\frac{MP}{PB}=1\implies \frac{62MP}{11BP}=1\implies \frac{MP}{BP}=\frac{11}{62}.</cmath>
 +
This implies that <math>\frac{MB}{BP}=1-\frac{MP}{BP}=\frac{51}{62}</math>. Then, by Menelaus on <math>\triangle AMP</math> and line <math>BC</math>, we have
 +
<cmath>\frac{AD}{DM}\cdot\frac{MB}{BP}\cdot\frac{PC}{CA}=1\implies \frac{PC}{CA}=\frac{31}{51}.</cmath>
 +
Therefore, <math>\frac{PC}{AP}=\frac{31}{51-31}=\frac{31}{20}.</math> The answer is <math>\boxed{051}</math>. -brainiacmaniac31
 +
 +
== Solution 7 (Visual) ==
 +
[[File:2011 AIME II 4.png|400px]]
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 +
 +
== Solution 8 (Cheese) ==
 +
Assume <math>ABC</math> is a right triangle at <math>A</math>. Line <math>AD = x</math> and <math>BC = \tfrac{-11}{20}x + 11</math>. These two lines intersect at <math>D</math> which have coordinates <math>(\frac{220}{31},\frac{220}{31})</math> and thus <math>M</math> has coordinates <math>(\frac{110}{31},\frac{110}{31})</math>. Thus, the line <math>BM = \tfrac{11}{51} \cdot (20-x)</math>. When <math>x = 0</math>, <math>P</math> has <math>y</math> coordinate equal to <math>\frac{11\cdot20}{51} \frac{AP + CP}{AP} = 1 + \frac{CP}{AP}</math> = <math>\tfrac{51}{20} = 1 + \frac{CP}{AP},</math> which equals <math>{\tfrac{31}{20}},</math> giving an answer of <math>\boxed{51}.</math>
 +
 +
== Solution 9 (Menelaus + Ceva's + Angle Bisector Theorem) ==
 +
We start by using Menelaus' theorem on <math>\triangle ABD</math> and <math>EC</math>.
 +
So, we see that <math>\frac{BC}{DC}\cdot\frac{DM}{AM}\cdot\frac{AE}{EB}=1</math>.
 +
By Angle Bisector theorem, <math>\frac{BC}{DC}=\frac{31}{11}</math>, and therefore after plugging in our values we get <math>\frac{AE}{EB}=\frac{11}{31}</math>.
 +
Then, by Ceva's on the whole figure, we have <math>\frac{CP}{PA}\cdot\frac{AE}{EB}\cdot\frac{BD}{DC}=1</math>.
 +
Plugging in our values, we get <math>\frac{CP}{PA}=\frac{31}{20}</math>, giving an answer of <math>\boxed{51}</math>.
 +
~ESAOPS
 +
 +
== Video Solution by OmegaLearn ==
 +
https://youtu.be/Gjt25jRiFns?t=314
 +
 +
~ pi_is_3.14
  
 
== See also ==
 
== See also ==

Latest revision as of 16:21, 17 November 2024

Problem 4

In triangle $ABC$, $AB=20$ and $AC=11$. The angle bisector of $\angle A$ intersects $BC$ at point $D$, and point $M$ is the midpoint of $AD$. Let $P$ be the point of the intersection of $AC$ and $BM$. The ratio of $CP$ to $PA$ can be expressed in the form $\dfrac{m}{n}$, where $m$ and $n$ are relatively prime positive integers. Find $m+n$.

Solution 1

[asy] pointpen = black; pathpen = linewidth(0.7); pair A = (0,0), C= (11,0), B=IP(CR(A,20),CR(C,18)), D = IP(B--C,CR(B,20/31*abs(B-C))), M = (A+D)/2, P = IP(M--2*M-B, A--C), D2 = IP(D--D+P-B, A--C); D(MP("A",D(A))--MP("B",D(B),N)--MP("C",D(C))--cycle); D(A--MP("D",D(D),NE)--MP("D'",D(D2))); D(B--MP("P",D(P))); D(MP("M",M,NW)); MP("20",(B+D)/2,ENE); MP("11",(C+D)/2,ENE); [/asy] Let $D'$ be on $\overline{AC}$ such that $BP \parallel DD'$. It follows that $\triangle BPC \sim \triangle DD'C$, so \[\frac{PC}{D'C} = 1 + \frac{BD}{DC} = 1 + \frac{AB}{AC} = \frac{31}{11}\] by the Angle Bisector Theorem. Similarly, we see by the Midline Theorem that $AP = PD'$. Thus, \[\frac{CP}{PA} = \frac{1}{\frac{PD'}{PC}} = \frac{1}{1 - \frac{D'C}{PC}} = \frac{31}{20},\] and $m+n = \boxed{51}$.

Solution 2 (mass points)

Assign mass points as follows: by Angle-Bisector Theorem, $BD / DC = 20/11$, so we assign $m(B) = 11, m(C) = 20, m(D) = 31$. Since $AM = MD$, then $m(A) = 31$, and $\frac{CP}{PA} = \frac{m(A) }{ m(C)} = \frac{31}{20}$, so $m+n = \boxed{51}$.

Solution 3

By Menelaus' Theorem on $\triangle ACD$ with transversal $PB$, \[1 = \frac{CP}{PA} \cdot \frac{AM}{MD} \cdot \frac{DB}{CB} = \frac{CP}{PA} \cdot \left(\frac{1}{1+\frac{AC}{AB}}\right) \quad \Longrightarrow \quad \frac{CP}{PA} = \frac{31}{20}.\] So $m+n = \boxed{051}$.

Solution 4

We will use barycentric coordinates. Let $A = (1, 0, 0)$, $B = (0, 1, 0)$, $C = (0, 0, 1)$. By the Angle Bisector Theorem, $D = [0:11:20] = \left(0, \frac{11}{31}, \frac{20}{31}\right)$. Since $M$ is the midpoint of $AD$, $M = \frac{A + D}{2} = \left(\frac{1}{2}, \frac{11}{62}, \frac{10}{31}\right)$. Therefore, the equation for line BM is $20x = 31z$. Let $P = (x, 0, 1-x)$. Using the equation for $BM$, we get \[20x = 31(1-x)\] \[x = \frac{31}{51}\] Therefore, $\frac{CP}{PA} = \frac{1-x}{x} = \frac{31}{20}$ so the answer is $\boxed{051}$.

Solution 5

Let $DC=x$. Then by the Angle Bisector Theorem, $BD=\frac{20}{11}x$. By the Ratio Lemma, we have that $\frac{PC}{AP}=\frac{\frac{31}{11}x\sin\angle PBC}{20\sin\angle ABP}.$ Notice that $[\triangle BAM]=[\triangle BMD]$ since their bases have the same length and they share a height. By the sin area formula, we have that \[\frac{1}{2}\cdot20\cdot BM\cdot \sin\angle ABP=\frac{1}{2}\cdot \frac{20}{11}x\cdot BM\cdot\sin\angle PBC.\] Simplifying, we get that $\frac{\sin\angle PBC}{\sin\angle ABP}=\frac{11}{x}.$ Plugging this into what we got from the Ratio Lemma, we have that $\frac{PC}{AP}=\frac{31}{20}\implies\boxed{051.}$

Solution 6 (quick Menelaus)

First, we will find $\frac{MP}{BP}$. By Menelaus on $\triangle BDM$ and the line $AC$, we have \[\frac{BC}{CD}\cdot\frac{DA}{AM}\cdot\frac{MP}{PB}=1\implies \frac{62MP}{11BP}=1\implies \frac{MP}{BP}=\frac{11}{62}.\] This implies that $\frac{MB}{BP}=1-\frac{MP}{BP}=\frac{51}{62}$. Then, by Menelaus on $\triangle AMP$ and line $BC$, we have \[\frac{AD}{DM}\cdot\frac{MB}{BP}\cdot\frac{PC}{CA}=1\implies \frac{PC}{CA}=\frac{31}{51}.\] Therefore, $\frac{PC}{AP}=\frac{31}{51-31}=\frac{31}{20}.$ The answer is $\boxed{051}$. -brainiacmaniac31

Solution 7 (Visual)

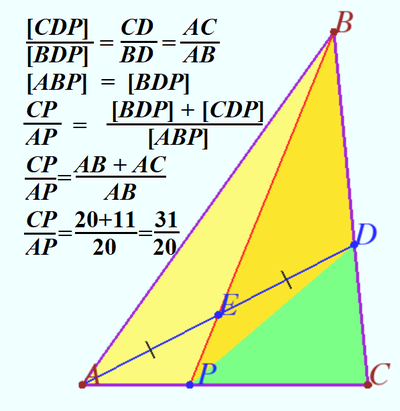2011 AIME II 4.png vladimir.shelomovskii@gmail.com, vvsss


Solution 8 (Cheese)

Assume $ABC$ is a right triangle at $A$. Line $AD = x$ and $BC = \tfrac{-11}{20}x + 11$. These two lines intersect at $D$ which have coordinates $(\frac{220}{31},\frac{220}{31})$ and thus $M$ has coordinates $(\frac{110}{31},\frac{110}{31})$. Thus, the line $BM = \tfrac{11}{51} \cdot (20-x)$. When $x = 0$, $P$ has $y$ coordinate equal to $\frac{11\cdot20}{51} \frac{AP + CP}{AP} = 1 + \frac{CP}{AP}$ = $\tfrac{51}{20} = 1 + \frac{CP}{AP},$ which equals ${\tfrac{31}{20}},$ giving an answer of $\boxed{51}.$

Solution 9 (Menelaus + Ceva's + Angle Bisector Theorem)

We start by using Menelaus' theorem on $\triangle ABD$ and $EC$. So, we see that $\frac{BC}{DC}\cdot\frac{DM}{AM}\cdot\frac{AE}{EB}=1$. By Angle Bisector theorem, $\frac{BC}{DC}=\frac{31}{11}$, and therefore after plugging in our values we get $\frac{AE}{EB}=\frac{11}{31}$. Then, by Ceva's on the whole figure, we have $\frac{CP}{PA}\cdot\frac{AE}{EB}\cdot\frac{BD}{DC}=1$. Plugging in our values, we get $\frac{CP}{PA}=\frac{31}{20}$, giving an answer of $\boxed{51}$. ~ESAOPS

Video Solution by OmegaLearn

https://youtu.be/Gjt25jRiFns?t=314

~ pi_is_3.14

See also

2011 AIME II (Problems • Answer Key • Resources)
Preceded by
Problem 3 		Followed by
Problem 5
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2011_AIME_II_Problems/Problem_4&oldid=234699"