Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "1987 AIME Problems"

m (→‎Problem 12)
m (→‎Problem 12)
 
(6 intermediate revisions by 6 users not shown)
Line 17: Line 17:
  
 
== Problem 4 ==
 
== Problem 4 ==
−
Find the area of the region enclosed by the graph of <math>|x-60|+|y|=|x/4|.</math>
+
Find the area of the region enclosed by the graph of <math>|x-60|+|y|=\left|\frac{x}{4}\right|.</math>
  
 
[[1987 AIME Problems/Problem 4|Solution]]
 
[[1987 AIME Problems/Problem 4|Solution]]
Line 61: Line 61:
  
 
== Problem 12 ==
 
== Problem 12 ==
−
Let m be the smallest integer whose cube root is of the form n+r, where n is a positive integer and r is a positive real number less than <math>1/1000</math>. Find n.
+
Let <math>m</math> be the smallest [[integer]] whose cube root is of the form <math>n+r</math>, where <math>n</math> is a [[positive integer]] and <math>r</math> is a positive real number less than <math>1/1000</math>. Find <math>n</math>.
  
 
[[1987 AIME Problems/Problem 12|Solution]]
 
[[1987 AIME Problems/Problem 12|Solution]]
Line 79: Line 79:
 
== Problem 14 ==
 
== Problem 14 ==
 
Compute
 
Compute
−
<center><math>\frac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}</math></center>.
+
<cmath>\frac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}.</cmath>
  
 
[[1987 AIME Problems/Problem 14|Solution]]
 
[[1987 AIME Problems/Problem 14|Solution]]
Line 91: Line 91:
  
 
== See also ==
 
== See also ==
 +
 +
{{AIME box|year=1987|before=[[1986 AIME Problems]]|after=[[1988 AIME Problems]]}}
 +
 
* [[American Invitational Mathematics Examination]]
 
* [[American Invitational Mathematics Examination]]
 
* [[AIME Problems and Solutions]]
 
* [[AIME Problems and Solutions]]

Latest revision as of 14:34, 22 August 2023

1987 AIME (Answer Key)
Printable version | AoPS Contest Collections • PDF

Instructions

  1. This is a 15-question, 3-hour examination. All answers are integers ranging from $000$ to $999$, inclusive. Your score will be the number of correct answers; i.e., there is neither partial credit nor a penalty for wrong answers.
  2. No aids other than scratch paper, rulers and compasses are permitted. In particular, graph paper, protractors, calculators and computers are not permitted.
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15

Problem 1

An ordered pair $(m,n)$ of non-negative integers is called "simple" if the addition $m+n$ in base $10$ requires no carrying. Find the number of simple ordered pairs of non-negative integers that sum to $1492$.

Solution

Problem 2

What is the largest possible distance between two points, one on the sphere of radius 19 with center $(-2,-10,5),$ and the other on the sphere of radius 87 with center $(12,8,-16)$?

Solution

Problem 3

By a proper divisor of a natural number we mean a positive integral divisor other than 1 and the number itself. A natural number greater than 1 will be called "nice" if it is equal to the product of its distinct proper divisors. What is the sum of the first ten nice numbers?

Solution

Problem 4

Find the area of the region enclosed by the graph of $|x-60|+|y|=\left|\frac{x}{4}\right|.$

Solution

Problem 5

Find $3x^2 y^2$ if $x$ and $y$ are integers such that $y^2 + 3x^2 y^2 = 30x^2 + 517$.

Solution

Problem 6

Rectangle $ABCD$ is divided into four parts of equal area by five segments as shown in the figure, where $XY = YB + BC + CZ = ZW = WD + DA + AX$, and $PQ$ is parallel to $AB$. Find the length of $AB$ (in cm) if $BC = 19$ cm and $PQ = 87$ cm.

AIME 1987 Problem 6.png

Solution

Problem 7

Let $[r,s]$ denote the least common multiple of positive integers $r$ and $s$. Find the number of ordered triples $(a,b,c)$ of positive integers for which $[a,b] = 1000$, $[b,c] = 2000$, and $[c,a] = 2000$.

Solution

Problem 8

What is the largest positive integer $n$ for which there is a unique integer $k$ such that $\frac{8}{15} < \frac{n}{n + k} < \frac{7}{13}$?

Solution

Problem 9

Triangle $ABC$ has right angle at $B$, and contains a point $P$ for which $PA = 10$, $PB = 6$, and $\angle APB = \angle BPC = \angle CPA$. Find $PC$.

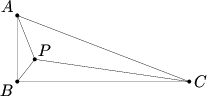
AIME 1987 Problem 9.png

Solution

Problem 10

Al walks down to the bottom of an escalator that is moving up and he counts 150 steps. His friend, Bob, walks up to the top of the escalator and counts 75 steps. If Al's speed of walking (in steps per unit time) is three times Bob's walking speed, how many steps are visible on the escalator at a given time? (Assume that this value is constant.)

Solution

Problem 11

Find the largest possible value of $k$ for which $3^{11}$ is expressible as the sum of $k$ consecutive positive integers.

Solution

Problem 12

Let $m$ be the smallest integer whose cube root is of the form $n+r$, where $n$ is a positive integer and $r$ is a positive real number less than $1/1000$. Find $n$.

Solution

Problem 13

A given sequence $r_1, r_2, \dots, r_n$ of distinct real numbers can be put in ascending order by means of one or more "bubble passes". A bubble pass through a given sequence consists of comparing the second term with the first term, and exchanging them if and only if the second term is smaller, then comparing the third term with the second term and exchanging them if and only if the third term is smaller, and so on in order, through comparing the last term, $r_n$, with its current predecessor and exchanging them if and only if the last term is smaller.

The example below shows how the sequence 1, 9, 8, 7 is transformed into the sequence 1, 8, 7, 9 by one bubble pass. The numbers compared at each step are underlined.

$\underline{1 \quad 9} \quad 8 \quad 7$
$1 \quad {}\underline{9 \quad 8} \quad 7$
$1 \quad 8 \quad \underline{9 \quad 7}$
$1 \quad 8 \quad 7 \quad 9$

Suppose that $n = 40$, and that the terms of the initial sequence $r_1, r_2, \dots, r_{40}$ are distinct from one another and are in random order. Let $p/q$, in lowest terms, be the probability that the number that begins as $r_{20}$ will end up, after one bubble pass, in the $30^{\mbox{th}}$ place. Find $p + q$.

Solution

Problem 14

Compute \[\frac{(10^4+324)(22^4+324)(34^4+324)(46^4+324)(58^4+324)}{(4^4+324)(16^4+324)(28^4+324)(40^4+324)(52^4+324)}.\]

Solution

Problem 15

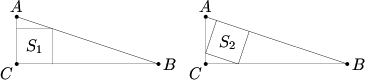
Squares $S_1$ and $S_2$ are inscribed in right triangle $ABC$, as shown in the figures below. Find $AC + CB$ if area $(S_1) = 441$ and area $(S_2) = 440$.

AIME 1987 Problem 15.png

Solution

See also

1987 AIME (Problems • Answer Key • Resources)
Preceded by
1986 AIME Problems 		Followed by
1988 AIME Problems
1 • 2 • 3 • 4 • 5 • 6 • 7 • 8 • 9 • 10 • 11 • 12 • 13 • 14 • 15
All AIME Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=1987_AIME_Problems&oldid=197307"