Art of Problem Solving
AoPS Online
Math texts, online classes, and more
for students in grades 5-12.
Visit AoPS Online ‚
Books for Grades 5-12 Online Courses
Beast Academy
Engaging math books and online learning
for students ages 6-13.
Visit Beast Academy ‚
Books for Ages 6-13 Beast Academy Online
AoPS Academy
Small live classes for advanced math
and language arts learners in grades 2-12.
Visit AoPS Academy ‚
Find a Physical Campus Visit the Virtual Campus

Difference between revisions of "2016 USAMO Problems/Problem 5"

(Created page with "==Problem== An equilateral pentagon <math>AMNPQ</math> is inscribed in triangle <math>ABC</math> such that <math>M\in\overline{AB},</math> <math>Q\in\overline{AC},</math> and ...")
 
m
 
(11 intermediate revisions by 5 users not shown)
Line 3: Line 3:
  
 
Prove that <math>\overline{OI}</math> is parallel to <math>\ell,</math> where <math>O</math> is the circumcenter of triangle <math>ABC,</math> and <math>I</math> is the incenter of triangle <math>ABC.</math>
 
Prove that <math>\overline{OI}</math> is parallel to <math>\ell,</math> where <math>O</math> is the circumcenter of triangle <math>ABC,</math> and <math>I</math> is the incenter of triangle <math>ABC.</math>
−
==Solution==
+
==Solution 1==
−
{{solution}}
+
 
 +
Let  <math>D</math> be the intersection of line <math>AI</math> and the circumcircle of <math>\Delta ABC</math> (other than <math>A</math>), then <math>OD\perp BC</math>. Let <math>R</math> be the point such that <math>NPQR</math> is a rhombus. It follows that <math>OD\perp QR</math>.
 +
 
 +
Since <math>AM=AQ</math>, <math>AI\perp MQ</math>, or <math>DI\perp MQ</math>. It follows that <math>\angle ODI=\angle RQM</math>.
 +
 
 +
Since <math>BO=OD</math>, <math>MA=AQ</math>, <math>\angle BOD=\angle MAQ</math>, it follows that <math>\Delta BOD\sim\Delta MAQ</math>, so <math>AQ/MQ=OD/BD</math>.
 +
 
 +
It is given that <math>AQ=NP=RQ</math>, and by basic properties of the incenter, <math>ID=BD</math>. Therefore, <math>RQ/MQ=OD/ID</math>, so <math>\Delta RQM\sim\Delta ODI</math>.
 +
Since the rotation between the two triangles in 90 degrees, <math>OI\perp MR</math>. However, <math>l</math> is parallel to the bisector of <math>MNR</math>, which is perpendicular to <math>MR</math>, so we are done.
 +
 
 +
==Solution 2==
 +
 
 +
Write <math>\angle{JKL} = K</math> for all <math>J,K,L</math> chosen as distinct vertices of triangle <math>ABC</math>. Define <math>a, b, c</math> as sides opposite to angles <math>A, B</math>, and <math>C</math>, respectively. Place the triangle in the Euclidean plane with <math>A</math> at the origin and <math>C</math> on the positive x-axis. Assume without loss of generality that C is acute.
 +
 
 +
Consider the sides of the pentagon as vectors and note that <cmath>\overrightarrow{AM} + \overrightarrow{MN} + \overrightarrow{NP} = \overrightarrow{AQ} + \overrightarrow{QP} \qquad (1)</cmath>
 +
 
 +
Define <math>\delta</math> and <math>\gamma</math> as the angles made between the positive x-axis and <math>\overrightarrow{MN}</math> and <math>\overrightarrow{QP}</math>, respectively. Considering the x and y coordinates of the vectors in <math>(1)</math>, it follows that
 +
<cmath>\cos \delta - \cos \gamma = 1 - \cos A - \cos C    \qquad (2)</cmath>
 +
<cmath>\sin \delta - \sin \gamma = \sin C - \sin A        \qquad (3)</cmath>
 +
 
 +
Suppose <math>\sin C - \sin A = 0</math>. Then <math>A = C</math>, and the triangle is isosceles. In this case, it is clear by symmetry that <math>\overline{OI}</math> is vertical. Further, since point <math>S</math> exists, <math>\delta \neq \gamma</math>, so <math>\delta + \gamma = 180</math> and <math>\overrightarrow{MN} + \overrightarrow{QP}</math> must be vertical as well.
 +
 
 +
For the remainder of the proof, assume <math>\sin C \neq \sin A</math>. Note that <cmath>\frac{\cos y – \cos x}{\sin x - \sin y} = \frac{ (\cos y - \cos x)(\sin x + \sin y)}{ (\sin x - \sin y)(\sin x + \sin y)} = \frac {\sin x + \sin y}{\cos x + \cos y} </cmath> whenever <math>x, y \in \mathbb{R}</math> and <math>\sin x \neq \sin y</math>. Note further that the slope of the line defined by the vector formed by summing vectors <math>(\cos x, \sin x)</math> and <math>(\cos y, \sin y)</math> is this expression. Since <math>\ell</math> is parallel to <math>\overrightarrow{MN} + \overrightarrow{QP}</math>, the slope of <math>\ell</math> can be formed by dividing expressions in <math>(2)</math> and <math>(3)</math> and inverting the sign: <cmath>\frac{\cos A + \cos C – 1}{\sin C - \sin A} \qquad (4)</cmath>
 +
 
 +
Determine the coordinates of <math>I</math> by drawing perpendiculars from <math>I</math> to the sides and vertices of the triangle. By exploiting congruence between pairs of right triangles that share a vertex, one can partition <math>a,b,c</math> into <math>p+q, p+r, q+r</math> where <math>p,q,r</math> are bases of these triangles that lie on the sides of triangle <math>ABC</math>. From here it is clear that <math>I = \left(\frac{b + c – a}{2} , \frac{b + c – a}{2}\tan(A / 2)\right)</math>.
 +
 
 +
To find the coordinates of <math>O</math>, note that <math>\angle{OJK} + \angle{OJL} = \angle{J}</math> and that <math>\angle {OJK} = \angle{OKJ}</math> in any acute triangle <math>JKL</math>. It easily follows that <math>\angle{OJK} = 90 – L</math>. Note also that the perpendicular from <math>O</math> to <math>\overline{JK}</math> bisects <math>\overline{JK}</math>. Hence, <cmath>O = \left(\frac{b}{2},\frac{b}{2} \cot B\right) \qquad (5)</cmath> if triangle <math>ABC</math> is acute.
 +
 
 +
If triangle <math>JKL</math> is obtuse at <math>\angle J</math>, then it can be similarly shown that <math>\angle{OKL} = \angle{OLK} = J – 90</math> but that the remaining angles of this form are still <math>90-L</math> and <math>90-K</math>. It easily follows that <math>(5)</math> holds if <math>\angle A</math> is obtuse. If <math>\angle B</math> is obtuse then <math>\angle OAC = B – 90</math> and the <math>y</math> coordinate of <math>O</math> is <math>-\frac{b}{2} \tan{B-90}</math>. From this, <math>(5)</math> follows in this case as well.
 +
 
 +
We can conclude the slope of <math>\overline {OI}</math> is <cmath>\left(\frac{b \cot {B} – (b + c – a) \tan(A/2)}{a – c}\right) = \left( \frac {\cos B – \tan{(A/2)}\sin B}{\sin A - \sin C}\right) + \tan(A/2)  \quad (6)</cmath> by the Law of Sines and rearrangement.
 +
 
 +
Setting <math>(6) = (4)</math> is equivalent to <cmath>1 - \cos A - \cos C = \cos B + \tan(A/2)(\sin A - \sin B - \sin C)</cmath>
 +
 
 +
Since <math>\tan(A/2) = \frac{\sin A}{1 + \cos A}</math>, this equation is equivalent to <cmath>(1 + \cos A)(\cos A + \cos B + \cos C – 1) = (\sin A)(\sin B + \sin C - \sin A)</cmath>
 +
 
 +
This equation is equivalent to <cmath>\cos(A + B) + \cos(A + C) + \cos B + \cos C = 0</cmath> which is evident.
 +
 
 +
==Solution 3==
 +
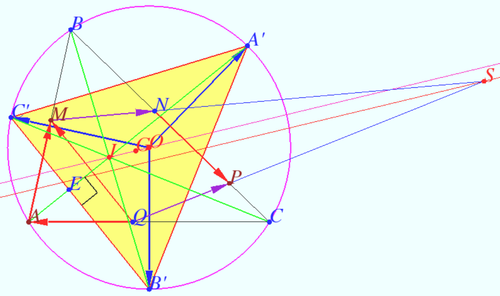
[[File:2016 USAMO 5a.png|500px|right]]
 +
Let <math>A', B',</math> and <math>C'</math> be the arc midpoints of <math>BC, CA, AB,</math> respectively. Let <math>E</math> be crosspoint of <math>AI</math> and <math>B'C'.</math>
 +
 
 +
Therefore <math>O</math> is the circumcenter of triangle <math>A'B'C'.</math>
 +
 
 +
Points <math>A, I, E,</math> and <math>A'</math> are collinear.
 +
<math>\angle A'EB' = \frac {\overset{\Large\frown} {AC'}+\overset{\Large\frown} {B'C} +\overset{\Large\frown} {CA'}}{2} = 90^\circ \implies AA' \perp B'C'</math>
 +
<math>\implies I</math> is orthocenter of <math>\triangle A'B'C' \implies</math>
 +
 
 +
<math>IO</math> is the Euler line of <math>\triangle A'B'C'.</math>
 +
 
 +
Let <math>G</math> be the centroid of <math>\triangle A'B'C' \implies G </math> lies on line <math>IO</math>
 +
<math>\implies \overline {OG} = \frac {\overline{OA'} + \overline{OB'} + \overline{OC'}}{3}</math> is paraller to <math>\overline{OI}.</math>
 +
<math>\overline{OB'} \perp \overline{AC} \implies \overline{OB'} \perp \overline{QA}.</math>
 +
[[File:2016 USAMO 5.png|250px|right]]
 +
Similarly <math>\overline{OC'} \perp \overline{AM}, \overline{OA'} \perp \overline{NP},</math> rotation from <math>\overline{OA'}</math> to <math>\overline{NP}</math>, from <math>\overline{OB'}</math> to <math>\overline{QA},</math> and from <math>\overline{OC'}</math> to <math>\overline{AM}</math> is in clockwise direction, <math>|\overline{QA}|=| \overline{AM}| =|\overline{NP}|, |\overline{OA'}| = |\overline{OB'}| = |\overline{OC'}| \implies</math>
 +
 
 +
<math>\overline{QA} + \overline{AM} + \overline{NP} = \overline{QM} + \overline{NP}</math> is perpendicular to <math>|\overline{OI}.</math>
 +
 
 +
<math>|\overline{MN}| = |\overline{QP}|</math> therefore in accordance with <i><b>Claim</b></i> <math>\overline{MN} + \overline{QP}</math> is parallel to <math>\overline{OI}.</math>
 +
 +
This sum is parallel to <math>\ell,</math>, so we are done.
 +
 
 +
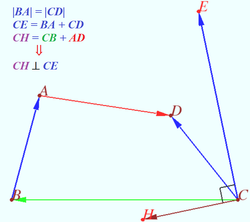
<i><b>Claim</b></i>
 +
 
 +
Let <math>|\overline{BA}|= |\overline{CD}|, \overline{CB} + |\overline{BA} + |\overline{AD} = |\overline{CD}.</math>
 +
Then <math>(\overline{BA} + \overline{CD}) \perp (\overline{CB} + \overline{AD}).</math>
 +
 
 +
<i><b>Proof</b></i>
 +
 
 +
<math>(\overline{BA} + \overline{CD}) \cdot (\overline{CB} + \overline{AD}) = (\overline{BA} + \overline{CD}) \cdot (\overline{CB} + \overline{CD} – \overline{CB} – \overline{BA}) = |\overline{CD}|^2 – |\overline{BA}|^2 = 0.</math>
 +
 
 +
'''vladimir.shelomovskii@gmail.com, vvsss'''
 +
 
 +
==Video Solution by MOP 2024==
 +
https://youtu.be/OnGdqIvOBd4
 +
 
 +
~r00tsOfUnity
  
−
{{MAA Notice}}
 
 
==See also==
 
==See also==
 
{{USAMO newbox|year=2016|num-b=4|num-a=6}}
 
{{USAMO newbox|year=2016|num-b=4|num-a=6}}
 +
{{MAA Notice}}

Latest revision as of 23:09, 11 October 2023

Problem

An equilateral pentagon $AMNPQ$ is inscribed in triangle $ABC$ such that $M\in\overline{AB},$ $Q\in\overline{AC},$ and $N, P\in\overline{BC}.$ Let $S$ be the intersection of lines $MN$ and $PQ.$ Denote by $\ell$ the angle bisector of $\angle MSQ.$

Prove that $\overline{OI}$ is parallel to $\ell,$ where $O$ is the circumcenter of triangle $ABC,$ and $I$ is the incenter of triangle $ABC.$

Solution 1

Let $D$ be the intersection of line $AI$ and the circumcircle of $\Delta ABC$ (other than $A$), then $OD\perp BC$. Let $R$ be the point such that $NPQR$ is a rhombus. It follows that $OD\perp QR$.

Since $AM=AQ$, $AI\perp MQ$, or $DI\perp MQ$. It follows that $\angle ODI=\angle RQM$.

Since $BO=OD$, $MA=AQ$, $\angle BOD=\angle MAQ$, it follows that $\Delta BOD\sim\Delta MAQ$, so $AQ/MQ=OD/BD$.

It is given that $AQ=NP=RQ$, and by basic properties of the incenter, $ID=BD$. Therefore, $RQ/MQ=OD/ID$, so $\Delta RQM\sim\Delta ODI$. Since the rotation between the two triangles in 90 degrees, $OI\perp MR$. However, $l$ is parallel to the bisector of $MNR$, which is perpendicular to $MR$, so we are done.

Solution 2

Write $\angle{JKL} = K$ for all $J,K,L$ chosen as distinct vertices of triangle $ABC$. Define $a, b, c$ as sides opposite to angles $A, B$, and $C$, respectively. Place the triangle in the Euclidean plane with $A$ at the origin and $C$ on the positive x-axis. Assume without loss of generality that C is acute.

Consider the sides of the pentagon as vectors and note that \[\overrightarrow{AM} + \overrightarrow{MN} + \overrightarrow{NP} = \overrightarrow{AQ} + \overrightarrow{QP} \qquad (1)\]

Define $\delta$ and $\gamma$ as the angles made between the positive x-axis and $\overrightarrow{MN}$ and $\overrightarrow{QP}$, respectively. Considering the x and y coordinates of the vectors in $(1)$, it follows that \[\cos \delta - \cos \gamma = 1 - \cos A - \cos C \qquad (2)\] \[\sin \delta - \sin \gamma = \sin C - \sin A \qquad (3)\]

Suppose $\sin C - \sin A = 0$. Then $A = C$, and the triangle is isosceles. In this case, it is clear by symmetry that $\overline{OI}$ is vertical. Further, since point $S$ exists, $\delta \neq \gamma$, so $\delta + \gamma = 180$ and $\overrightarrow{MN} + \overrightarrow{QP}$ must be vertical as well.

For the remainder of the proof, assume $\sin C \neq \sin A$. Note that \[\frac{\cos y – \cos x}{\sin x - \sin y} = \frac{ (\cos y - \cos x)(\sin x + \sin y)}{ (\sin x - \sin y)(\sin x + \sin y)} = \frac {\sin x + \sin y}{\cos x + \cos y}\] whenever $x, y \in \mathbb{R}$ and $\sin x \neq \sin y$. Note further that the slope of the line defined by the vector formed by summing vectors $(\cos x, \sin x)$ and $(\cos y, \sin y)$ is this expression. Since $\ell$ is parallel to $\overrightarrow{MN} + \overrightarrow{QP}$, the slope of $\ell$ can be formed by dividing expressions in $(2)$ and $(3)$ and inverting the sign: \[\frac{\cos A + \cos C – 1}{\sin C - \sin A} \qquad (4)\]

Determine the coordinates of $I$ by drawing perpendiculars from $I$ to the sides and vertices of the triangle. By exploiting congruence between pairs of right triangles that share a vertex, one can partition $a,b,c$ into $p+q, p+r, q+r$ where $p,q,r$ are bases of these triangles that lie on the sides of triangle $ABC$. From here it is clear that $I = \left(\frac{b + c – a}{2} , \frac{b + c – a}{2}\tan(A / 2)\right)$.

To find the coordinates of $O$, note that $\angle{OJK} + \angle{OJL} = \angle{J}$ and that $\angle {OJK} = \angle{OKJ}$ in any acute triangle $JKL$. It easily follows that $\angle{OJK} = 90 – L$. Note also that the perpendicular from $O$ to $\overline{JK}$ bisects $\overline{JK}$. Hence, \[O = \left(\frac{b}{2},\frac{b}{2} \cot B\right) \qquad (5)\] if triangle $ABC$ is acute.

If triangle $JKL$ is obtuse at $\angle J$, then it can be similarly shown that $\angle{OKL} = \angle{OLK} = J – 90$ but that the remaining angles of this form are still $90-L$ and $90-K$. It easily follows that $(5)$ holds if $\angle A$ is obtuse. If $\angle B$ is obtuse then $\angle OAC = B – 90$ and the $y$ coordinate of $O$ is $-\frac{b}{2} \tan{B-90}$. From this, $(5)$ follows in this case as well.

We can conclude the slope of $\overline {OI}$ is \[\left(\frac{b \cot {B} – (b + c – a) \tan(A/2)}{a – c}\right) = \left( \frac {\cos B – \tan{(A/2)}\sin B}{\sin A - \sin C}\right) + \tan(A/2) \quad (6)\] by the Law of Sines and rearrangement.

Setting $(6) = (4)$ is equivalent to \[1 - \cos A - \cos C = \cos B + \tan(A/2)(\sin A - \sin B - \sin C)\]

Since $\tan(A/2) = \frac{\sin A}{1 + \cos A}$, this equation is equivalent to \[(1 + \cos A)(\cos A + \cos B + \cos C – 1) = (\sin A)(\sin B + \sin C - \sin A)\]

This equation is equivalent to \[\cos(A + B) + \cos(A + C) + \cos B + \cos C = 0\] which is evident.

Solution 3

2016 USAMO 5a.png

Let $A', B',$ and $C'$ be the arc midpoints of $BC, CA, AB,$ respectively. Let $E$ be crosspoint of $AI$ and $B'C'.$

Therefore $O$ is the circumcenter of triangle $A'B'C'.$

Points $A, I, E,$ and $A'$ are collinear. $\angle A'EB' = \frac {\overset{\Large\frown} {AC'}+\overset{\Large\frown} {B'C} +\overset{\Large\frown} {CA'}}{2} = 90^\circ \implies AA' \perp B'C'$ $\implies I$ is orthocenter of $\triangle A'B'C' \implies$

$IO$ is the Euler line of $\triangle A'B'C'.$

Let $G$ be the centroid of $\triangle A'B'C' \implies G$ lies on line $IO$ $\implies \overline {OG} = \frac {\overline{OA'} + \overline{OB'} + \overline{OC'}}{3}$ is paraller to $\overline{OI}.$ $\overline{OB'} \perp \overline{AC} \implies \overline{OB'} \perp \overline{QA}.$

2016 USAMO 5.png

Similarly $\overline{OC'} \perp \overline{AM}, \overline{OA'} \perp \overline{NP},$ rotation from $\overline{OA'}$ to $\overline{NP}$, from $\overline{OB'}$ to $\overline{QA},$ and from $\overline{OC'}$ to $\overline{AM}$ is in clockwise direction, $|\overline{QA}|=| \overline{AM}| =|\overline{NP}|, |\overline{OA'}| = |\overline{OB'}| = |\overline{OC'}| \implies$

$\overline{QA} + \overline{AM} + \overline{NP} = \overline{QM} + \overline{NP}$ is perpendicular to $|\overline{OI}.$

$|\overline{MN}| = |\overline{QP}|$ therefore in accordance with Claim $\overline{MN} + \overline{QP}$ is parallel to $\overline{OI}.$

This sum is parallel to $\ell,$, so we are done.

Claim

Let $|\overline{BA}|= |\overline{CD}|, \overline{CB} + |\overline{BA} + |\overline{AD} = |\overline{CD}.$ Then $(\overline{BA} + \overline{CD}) \perp (\overline{CB} + \overline{AD}).$

Proof

$(\overline{BA} + \overline{CD}) \cdot (\overline{CB} + \overline{AD}) = (\overline{BA} + \overline{CD}) \cdot (\overline{CB} + \overline{CD} – \overline{CB} – \overline{BA}) = |\overline{CD}|^2 – |\overline{BA}|^2 = 0.$

vladimir.shelomovskii@gmail.com, vvsss

Video Solution by MOP 2024

https://youtu.be/OnGdqIvOBd4

~r00tsOfUnity

See also

2016 USAMO (Problems • Resources)
Preceded by
Problem 4 		Followed by
Problem 6
1 • 2 • 3 • 4 • 5 • 6
All USAMO Problems and Solutions

The problems on this page are copyrighted by the Mathematical Association of America's American Mathematics Competitions. AMC logo.png

Retrieved from "https://artofproblemsolving.com/wiki/index.php?title=2016_USAMO_Problems/Problem_5&oldid=199545"